Dieses Programm wurde zur Lösung der häufigsten thermomechanischen und wärmetechnischen Aufgaben entwickelt, mit denen Konstrukteure konfrontiert werden.
Das Programm löst Aufgaben aus den folgenden Bereichen:
1. Energie: Erwärmung und Abkühlung, Zustandsänderung, Heizwert von Brennstoffen
2. Ideales Gas: Zustand und Zustandsänderung, thermodynamisches System
3. Wärmeübertragung durch Verbundwände: Leitung, Strahlung, Konvektion
4. Lösungen für Rippenwände und Rohrbündel
5. Longitudinale Temperaturänderung in Rohrleitungen: Temperaturänderung und Abkühlzeit in Behältern
6. Wärmetauscher
7. Wärmeübertragung durch Strahlung
8. Sonnenstrahlungsleistung: Dauer, Zeit, Position, Umgebung, Flächenausrichtung usw.
9. Datenaufbereitung zur Verwendung des Add-ons "Löser"
Die Berechnungen umfassen Hunderte von vordefinierten Materialien, Flüssigkeiten und Gasen, ein Periodensystem der Elemente, Einheitenumrechnungen und mehr. Eine Vielzahl von gelösten Beispielen ist ebenfalls verfügbar.
In den Berechnungen werden Daten, Verfahren, Algorithmen und Informationen aus Fachliteratur, Normen und Firmenkatalogen verwendet.
[01] YUNUS A. ÇENGEL, AFSHIN J. GHAJAR: Heat and Mass Transfer: Fundamentals
& Applications, 5th Edition, McGraw-Hill Education.
[02] YUNUS A. ÇENGEL: Heat Transfer a Practical Approach, Second Edition.
[03] MORAN, M.J., SHAPIO, H.N.: Fundamentals of engineering thermodynamics. 8th
Edition New York: John Wiley a sons, 1990.
[04] DEWITT, BERGMAN, LAVINE: Fundamentals of Heat and Mass Transfer 6th Edition
[05] WARREN M.ROHSENOW, JAMES R.HARTNETT, YOUNG I.CHO: Handbook of Heat
Transfer, 3th Edition, McGraw-Hill
[06] SCHLUNDER, BELL, HEWITT, SPALDING: Heat Exchanger
Design Handbook, VDI-Verlag GmbH, 1983.
[07] LOIS THEODORE: Heat Transfer Applications for the
Practicing Engineer, John Wiley & Sons, Inc., 2011.
[08] MYER KUTZ: Heat-Transfer Calculations,
McGraw-Hill
[09] HOLMAN, J.P.: Heat Transfer, 10th. Edition, New
York: McGraw-Hill
[10] HOLMAN, J.P. Thermodynamics. 4th. New York:
McGraw-Hill Book Company, 1988. 780 s. ISBN 0-07-029633-2.
[11] MOHAMED M. EL-AWAD: Optimisation Analyses of
Fluid- Thermal Systems Using Excel,
[12] FRANK KREITH, RAJ MANGLIK, MARK BOHN: Principles
of Heat Transfer, Cengage Learning, Inc., 2011
[13] HORÁK VLADIMÍR, STŘEDA IVO: Mechanika tekutin
- Termomechanika, Strojírenská příručka, Scientia sro.
[14] RANEVI,K. Termodynamické tabulky. 1.vyd.
Bratislava: ALFA 1984. 313s. [L5] HAEK, P. Tabulky pro tepelnou techniku. 1
.vyd. VB Ostrava, 1980, 247 s.
[15] SAZIMA,M., KMON1OEK,V., SCHNELER,J. Teplo. 1.vyd.
Praha: SNTL, 1989. 588 s. Technický průvodce. ISBN 80-03-00043-2.
[16] M.A.MICHEJEV: Základy sdílení tepla, Průmyslové
vydavatelství, 1952
[17] PETRAK,J., DVOAK, Z., KLAZAR, L., SYNEK, V.
Chiadivo R134a, (1.vyd.) VUT, 1993. 72s.
[18] MIROSLAV JÍLEK, ZDENĚK RANDA: Termomechanika -
sbírka příkladů, ČVUT, 2004
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument"Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
E = m * ΔT * Cp
E ... Energie [J]
m ... Masse [kg]
ΔT ... Temperaturänderung [K]
Cp ... Spezifische Wärmekapazität [J/kg/K]
EM = m * CpM * 1000
EB = m * CpB * 1000
EM, EB ... Energie [J]
CpM ... Spezifische Wärmekapazität des Schmelzens [kJ/kg]
CpB ... Spezifische Wärmekapazität beim Sieden [kJ/kg]
E = m * HHV * (η / 100) * 1000000
E ... Energie [J]
m ... Masse des verbrannten Brennstoffs [kg]
HHV ... Verbrennungswärme [MJ/kg]
η ... Verbrennungswirkungsgrad [%]
Der Zustand eines thermodynamischen
Systems wird durch Zustandsgrößen charakterisiert. Die Beziehung zwischen diesen
Zustandsgrößen wird durch Zustandsgleichungen definiert.
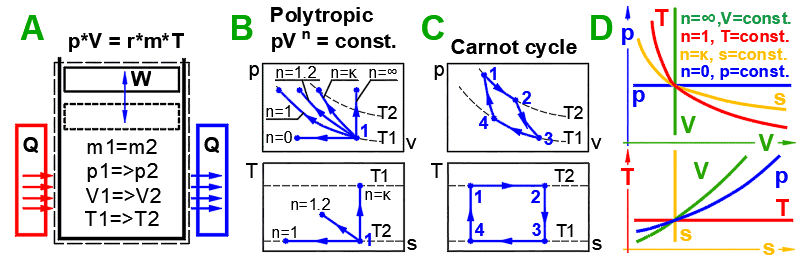
A ... Ein Beispiel für ein einfaches thermodynamisches System, das ideale Gas,
folgt der Gleichung: p*V=m*r*T.
B ... Reversible Prozesse können allgemeiner als polytrope Prozesse beschrieben
werden, bei denen die Wärmekapazität eines geschlossenen Systems konstant
bleibt. Bei einem polytropen Prozess ändern sich im Allgemeinen alle
Zustandsgrößen (p,V,T). Für einen polytropen Prozess in einem idealen Gas gilt
die Gleichung p*V^n = const. Die p-V und T-s Diagramme zeigen die
Änderungskurven für verschiedene n-Werte.
C ... Carnot-Kreisprozess. Ein Beispiel für eine ideale Wärmekraftmaschine, die
aus zwei isothermischen und zwei adiabatischen Prozessen besteht.
D ... Kurven grundlegender reversibler Zustandsänderungen.
p * V = m * r * T
r = R / M
M = m / N
p ... Absoluter Druck [Pa]
V ... Volumen [m^3]
m ... Masse [kg]
T ... Temperatur [°K]
R ... Universelle Gaskonstante R=8314.46261815324 [J/kmol/K]
M ... Molare Masse des Gases [kg/kmol] (Luft 28,966 kg/kmol)
N ... Menge des Stoffes [kmol]
r ... Spezifische Gaskonstante [J/kg/K] (Luft 287,0427 J/kg/K)
u = u0 + cv * (T - T0) [J/kg]
Δu = cv * (T2 - T1) [J/kg]
h = h0 + cp * (T - T0) [J/kg]
Δh = cp * (T2 - T1) [J/kg]
ds = s2 - s1 = cp * Ln(T2/T1) - r *
Ln(p2 / p1)
ds = s2 - s1 = cv * Ln(T2/T1) + r * Ln(v2 / v1)
cp - cv = r
cp ... Spezifische Wärmekapazität - konstanter Druck [J/kg/K]
cv ... Spezifische Wärmekapazität - konstantes Volumen [J/kg/K]
κ = cp / cv
cv = r / (κ - 1)
cp = κ * cv
p1 * V1 = p2 * V2
V1 / V2 = T1 / T2
Reversible Prozesse können als allgemeinere polytrope Prozesse betrachtet werden, für die:
p * V^n = konstant
T2 / T1 = (V1 / V2)^(n-1) = (p2 / p1)^((n-1)/n)
n ... Polytropischer Exponent [~]
Für ausgewählte Werte von n dann:
n=0 , p=const, Isobaric, (dp=0, wt=0, q=Δh, w=Δh-Δu)
n=1 , T=const, Isothermic, (dT=0, Δu=Δh=0, q=w=wt)
n=κ , s=konstant, isoentropisch, (ds=0, q=0, w=-Δu, wt=-Δh)
n=∞ , v=konstant, isochorisch, (dv=0, w=0, q=Δu, wt=Δu-Δh)
n = ln(p2 / p1) / (ln(p2 / p1) - ln(T2 / T1))
n = (ln(V2 / V1) - ln(T2 / T1)) / ln(V2 / V1)
q = cn * (T2 - T1) [J/kg]
cn = cv * (n - κ) / (n - 1)
cn ... Polytrope spezifische Wärmekapazität [J/kg/K]
w = q - Δu [J/kg]
wt = q - Δh = n * w [J/kg]
Berechnung der Parameter eines Gases, das durch Mischen zweier Teile mit unterschiedlichen Parametern p,V,T eingeführt wird.
m = m1 + m2
p = m / M * R * T / V
V = V1 + V2
T = (m1 * T1 + m2 * T2) / (m1 + m2)
Dies ist eine häufig gestellte Aufgabe, sowohl im Maschinenbau als auch in anderen angrenzenden Bereichen. Selbstverständlich kann diese Problematik mit entsprechenden Simulationsprogrammen gelöst werden. Dennoch genügen für eine grundlegende Abschätzung und einen Großteil dieser Aufgaben meist einfache Berechnungen, die auf grundlegenden physikalischen Beziehungen basieren.
Die Einteilung erfolgt in Wärmeleitung, Konvektion und Strahlung. Die entsprechenden Beziehungen sind nachfolgend aufgeführt.
In den Berechnungen werden die folgenden Beziehungen für zusammengesetzte ebene, zylindrische und kugelförmige Wände (max. 10 Schichten) verwendet.
r(i) = D(i) / 2
q' = -λ * ΔT [W/m²]
qp' = (t(1) - t(n+1)) / Rp
qp' = (t(1) - t(n+1)) / Σ (b(i) / λ(i)) ..... [i=1...n]
R = Rp = Σ (b(i) / λ(i)) ..... [i=1...n]
qc' = (t(1) - t(n+1)) / Rc
qc' = (t(1) - t(n+1)) / (1/(2 * 3.14) * Σ ((1/λ(i)) * ln(r(i+1)/r(i)))) .....
[i=1...n]
Rc = (1 / (2 * 3.14159) * Σ ((1/λ(i)) * ln(r(i+1)/r(i)))) ..... [i=1...n]
R = Rc * (2 * 3.14159 * r(1))
qs' = (t(1) - t(n+1)) / Rs
qs' = (t(1) - t(n+1))
Rs = (1 / (4 * 3.14159) * Σ ((1/λ(i)) * (1/r(i) - 1/r(i+1))) ..... [i=1...n]
R = Rs * (4 * 3.14159 * r(1)²)
Der Wärmeübergang findet in der Grenzschicht nahe einer Wand statt, die sich aufgrund von Temperaturunterschieden bildet. Der Wärmeübergang selbst hängt dann von einer Vielzahl von Parametern ab (Fluideigenschaften, Strömungsart, Form der Fläche...).
Sowohl für die erzwungene Konvektion (Medium wird angetrieben) als auch für die freie Konvektion kann eine Vielzahl von Formeln verwendet werden, die auf Messungen und Wertapproximationen basieren (siehe Literatur). Die wichtigsten und häufig verwendeten Formeln werden in dieser Berechnung eingesetzt. Diese Formeln, ihre Gültigkeitsbereiche und die entsprechenden Diagramme sind unten aufgeführt. Für die Diagramme wurden solche dimensionsbehafteten Werte gewählt, die dem üblichen Gebrauch entsprechen können. In den Diagrammen werden zum Vergleich Luft und Wasser als die häufigsten Arbeitsmedien gewählt.
Für die Diagramme wurden folgende Einheiten gewählt: Temperatur [°C], Abmessungen [mm].
Die meisten verwendeten Beziehungen sind empirische Gleichungen, wobei die Ergebnisse durch Abhängigkeiten dimensionsloser Ähnlichkeitskriterien ausgedrückt werden.
Grashofer-Zahl Gr = 9,81 * L * β *
abs(T - Ts) / ν
Nusselt-Zahl Nu = hc * L / λ
Prandtl-Zahl Pr = (µ / Rho) / (λ / (Cp * Rho))
Rayleigh-Zahl Ra = Gr * Pr
Reynolds-Zahl Re = (L * V) / ν
Im Allgemeinen wird folgende Formel verwendet:
hc = (Nu * λ) / L
01a.
Rohrströmung - Kreis
(D,L): [Tdef = (T+Ts)/2, 0.1<Re<1e7] ...
(Strojírenská příručka, Graetz)
hc = (Nu *
λ) / D
Nu = (3.65 + (0.0668 * Re * Pr * (D/L)) / (1 + 0.045 * (Re * Pr *
(D/L))^(2/3))) * (μ / μs)^0.14 ..... [Re<2300]
Nu = 21 * (Pr * (D/L))^0.33 * (Re/2300)^(LOG(L/D)) ..... [Re*Pr*(D/L)>12, Pr>0.5,
L/D>30, 2300<Re<5000]
Nu = 3.66 * (Re/2300)^(2.3 + LOG(Pr) ..... [Re*Pr*(D/L)<12, Pr>0.5, L/D>30,
2300<Re<5000]
Nu = E * (0.023 * Pr^H * Re^0.8) * K ..... [0.5<Ts/Tdef<1 (°K),
1e4<Re<2e6]
Nu = E * (0.023 * Pr^H * Re^0.8) * K ..... [1<Ts/Tdef<3.5 (°K),
1e4<Re<2e6]
Koeficient H
H = 0.4 ..... T<Ts
H = 0.3 ..... T>Ts
Koeficient K
K = 1.27 - 0.27 * (Ts/Tdef) ..... [0.5<Ts/Tdef<1, Ts(°K),
T(°K)]
K = (Ts/Tdef)^(-0.55) ..... [1<Ts/Tdef<3.5, Ts(°K),
T(°K)]
Koeficient E
| ▼ Re... L/D ► | 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 1000 |
| 1.00E+04 | 1.65 | 1.50 | 1.34 | 1.23 | 1.17 | 1.13 | 1.07 | 1.03 | 1.00 | 1.00 |
| 2.00E+04 | 1.51 | 1.40 | 1.27 | 1.18 | 1.13 | 1.10 | 1.05 | 1.02 | 1.00 | 1.00 |
| 5.00E+04 | 1.34 | 1.27 | 1.18 | 1.13 | 1.10 | 1.08 | 1.04 | 1.02 | 1.00 | 1.00 |
| 1.00E+05 | 1.28 | 1.22 | 1.15 | 1.10 | 1.08 | 1.05 | 1.03 | 1.02 | 1.00 | 1.00 |
| 1.00E+06 | 1.14 | 1.11 | 1.08 | 1.05 | 1.04 | 1.03 | 1.02 | 1.01 | 1.00 | 1.00 |
| 1.00E+12 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
01b.
Rohrströmung -
Kreis
(D,L): [Tdef = (T+Ts)/2, 0.1<Re<1e7] ... (Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D
Nu = (3.65 + (0.0668 * Re * Pr * (D/L)) / (1 + 0.045 * (Re * Pr *
(D/L))^(2/3))) * (μ / μs)^0.14 ..... [Re<2100]
Nu = 0.023
* Re^0.8
*
Pr^H ..... [0.5<Pr<160,
6000<Re<1e7, L/D<60]
Koeficient H
H = 0.4 .... T<Ts
H = 0.3 .... T>Ts
01c.
Rohrströmung - Kreis
(D,L): [Tdef = (T+Ts)/2, 0.1<Re<1e7] ...
(Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ) / D
Nu = 1.86 * (Re * Pr * (D / L))^(1/3) * (μ / μs)^0.14
..... [Re<2100]
Nu =0.027 * Re^0.8 * Pr^(1/3) *
(μ / μs)^0.14 ..... [0.5
< Pr < 10000,
Re>2100]
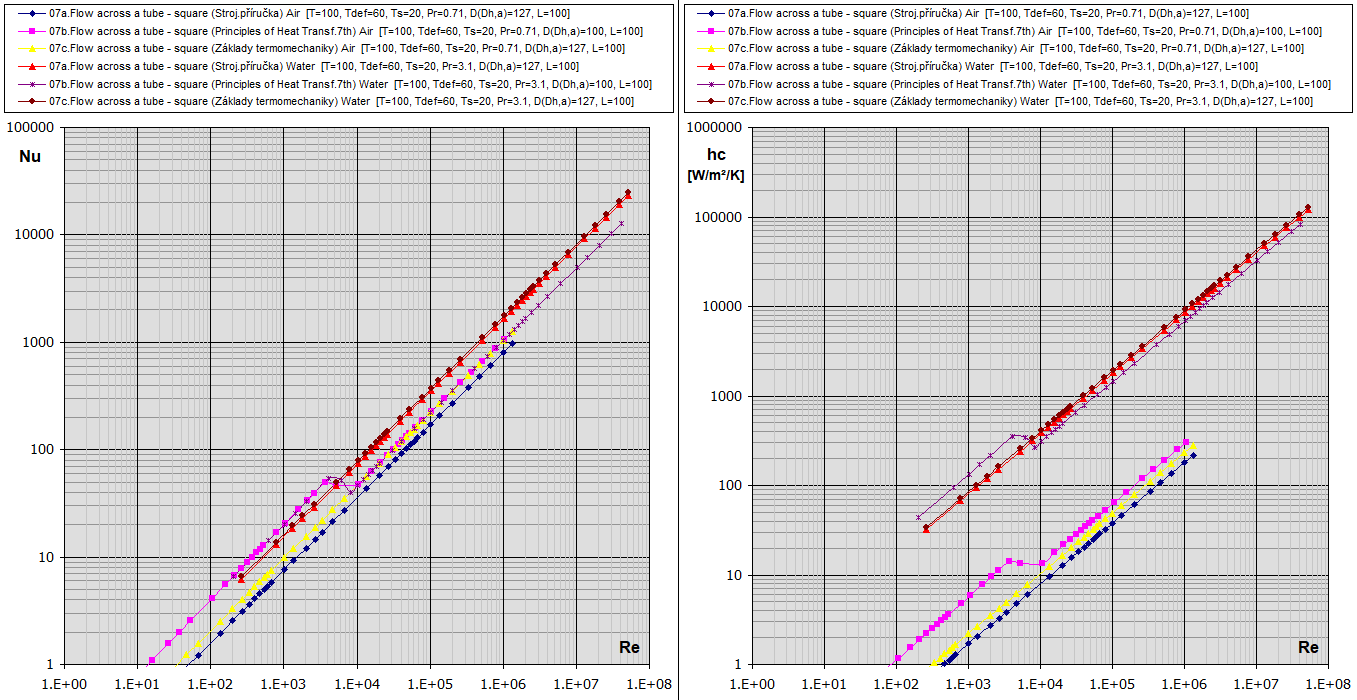
Re-Nu Graph für Luft und Wasser (T ... [°C], D,Dh,L ... [mm])
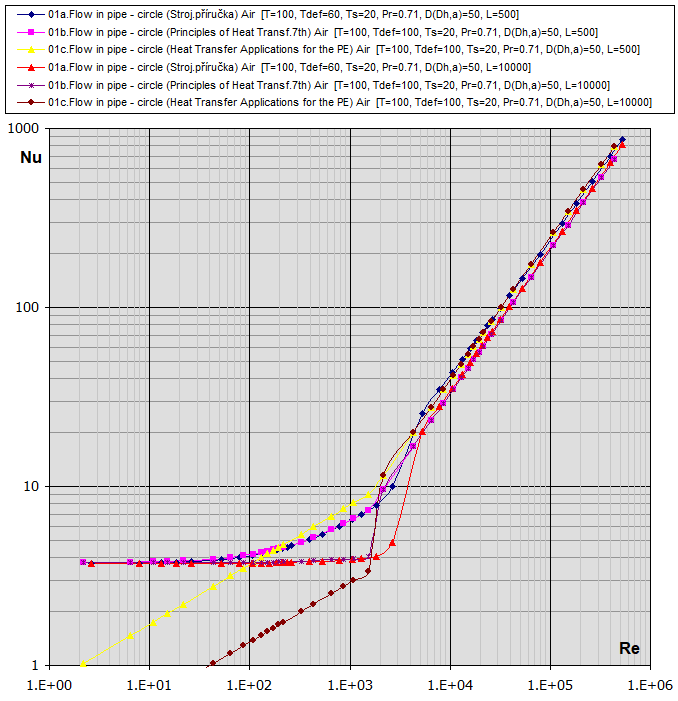
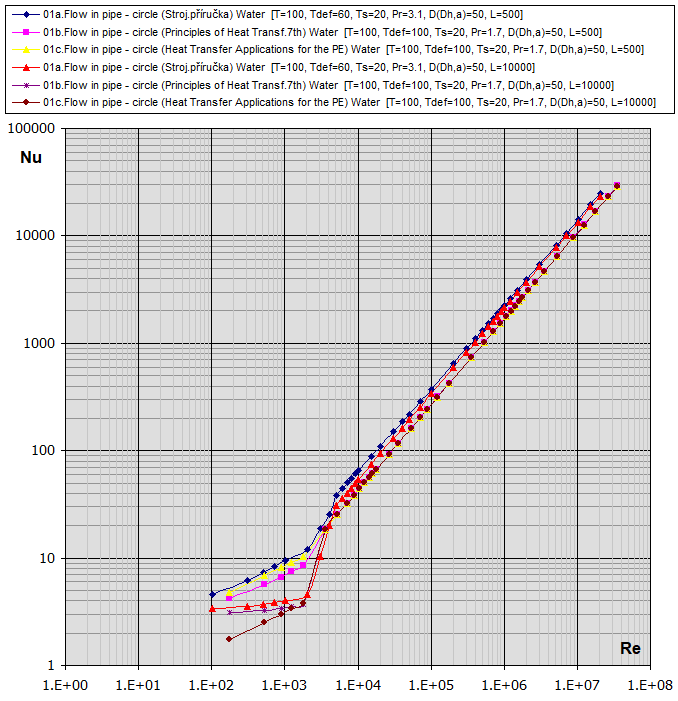

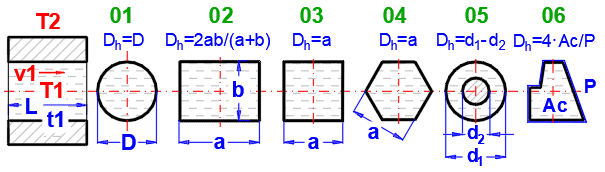
02.
Rohrströmung
- Rechteck (a,b) Dh = 2 * a * b / (a + b): [Tdef =
(T+Ts)/2, 0.1<Re<1e7] ...
(Strojírenská příručka)
03. Rohrströmung - quadratisch (a) Dh = a: [Tdef = (T+Ts)/2, 0.1<Re<1e7]
...
(Strojírenská příručka)
04. Rohrströmung - Sechseck (a) Dh = a: [Tdef = (T+Ts)/2, 0.1<Re<1e7] ...
(Strojírenská příručka)
06. Rohrströmung - beliebiger Querschnitt (Ac,P) Dh = 4 * Ac / P: [Tdef =
(T+Ts)/2, 0.1<Re<1e7] ...
(Strojírenská příručka)
hc = (Nu *
λ) / Dh
Nu = (3.65 + (0.0668 * Re * Pr * (Dh/L)) / (1 + 0.045 * (Re * Pr *
(Dh/L))^(2/3))) * (μ / μs)^0.14 .... [Re<2300]
Nu = 0.037*(1 + (Dh/L)^(2/3)) * (Re^0.75 - 180) * Pr^0.42 .... [Re>2300]
05. Rohrströmung - Zwischenringe (d1,d2) Dh = d1 - d2: [Tdef = (T+Ts)/2, 0.1<Re<1e7] ... (Gnielinski)
hc = (Nu * λ) / Dh
Laminare Strömung [Re<2300] durch Approximation aus der Tabelle:
| Durchmesserverhältnis | NuL1 | NuL2 |
| d2/d1 | (inside) | (outside) |
| 0.00 (tube) | - | 4.36 |
| 0.05 | 17.46 | 4.79 |
| 0.1 | 11.56 | 4.86 |
| 0.25 | 8.24 | 5.1 |
| 0.5 | 6.49 | 5.47 |
| 1.00 (planar slot) | 5.39 | 5.39 |
Turbulente Strömung [Re>4000]:
Für den inneren Kreis
NuT1=(0.86*(y)^(-0.16)) * NuS1
Für den äußeren Kreis
NuT2=(1 - ((1 - 0.86*(y)^0.16) / (3 * (y)))) * NuS2
y = d2 / d1 ... Verhältnis der Durchmesser
NuS = ((f / 8) * (Re - 1000) * Pr) / (1 + 12.7 * (f / 8)^0.5 * (Pr^(2/3) - 1))
f = (1.82 * log(Re) - 1.64)^(-2)
Strom im Übergangsbereich
(2300<Re<4000):
Lineare Interpolation von NuL und NuT
NuP = (1 - (Re - 2300)/1700) * NuL + ((Re - 2300)/1700) * NuT
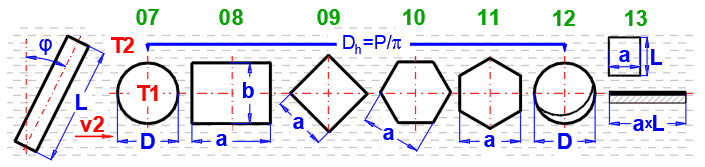
fcoeff ... Schräganströmung eines Rohres
| φ | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° |
| fcoeff | 1.00 | 1.00 | 0.99 | 0.95 | 0.86 | 0.75 | 0.63 | 0.50 |
07a.
Umströmung eines Rohres - Kreis (D): [Tdef = (T+Ts)/2, 0.5<Pr<1e3, 0.4<Re<4e5] ...
(Strojírenská příručka)
hc = (Nu *
λ) / D
* fcoeff
Nu =1.11 * K * Re^m * Pr^0.31
Nu =1.11 * K * Re^m * Pr^0.31 * (0.785 * (Ts/T)^(m/4) ..... for Gas
| Re | K | m |
| 0.4<Re<4 | 0.891 | 0.33 |
| 4<Re<40 | 0.821 | 0.385 |
| 40<Re<4e3 | 0.615 | 0.466 |
| 4e3<Re<4e4 | 0.174 | 0.618 |
| 4e4<Re<4e5 | 0.0239 | 0.805 |
07b.
Umströmung eines Rohres - Kreis (D): [Tdef =
T, 0.5<Pr<1e3,
0<Re<1e6] ...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D
* fcoeff
Nu =C * Re^m * Pr^n * (Pr/Prs)^0.25
n = 0.37 [Pr<10]
n= 0.36 [Pr>10]
| Re | C | m |
| Re<40 | 0.75 | 0.4 |
| 40<Re<1e3 | 0.51 | 0.5 |
| 1e3<Re<2e5 | 0.26 | 0.6 |
| 2e5<Re<1e6 | 0.076 | 0.7 |
07c.
Umströmung eines Rohres - Kreis
(D): [Tdef = (T+Ts)/2, 0.5<Pr<1e3, 0.04<Re<4e5] ...
(Heat Transfer Applications
for the Practicing Engineer)
hc = (Nu *
λ) / D
* fcoeff
Nu = C * Re^m * Pr^0.3333
| Re | C | m |
| 0.04<Re<4 | 0.989 | 0.33 |
| 4<Re<40 | 0.911 | 0.385 |
| 40<Re<4e3 | 0.683 | 0.466 |
| 4e3<Re<4e4 | 0.193 | 0.618 |
| 4e4<Re<4e5 | 0.027 | 0.805 |
Re-Nu Graph für Luft und Wasser
(T
... [°C], D,Dh,L ... [mm])
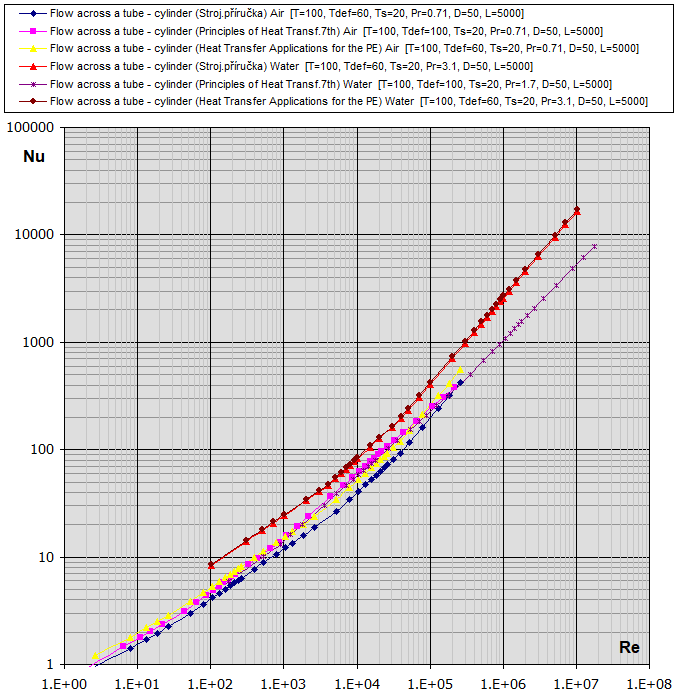

fcoeff ... Schräganströmung eines Rohres
| φ | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° |
| fcoeff | 1.00 | 1.00 | 0.99 | 0.95 | 0.86 | 0.75 | 0.63 | 0.50 |
08a. Umströmung eines
Rohres - Quadrat (a):
[Tdef = (T+Ts)/2, 5e3<Re<1e5,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =4
* a / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ) / Dh
* fcoeff
Nu =1.11 *
0.0921 * Re^0.675 * Pr^0.31
Nu =1.11 * 0.0921 * Re^0.675 * Pr^0.31 * (0.785 * (Ts/T)^(0.675/4) ..... for Gas
08b. Umströmung eines
Rohres - Quadrat (a):
[Tdef = T, 2.5e3<Re<1e5,
0.6<Pr<0.85] ...
(Principles of Heat Transfer
7th. edtion)
Dh = a
Re =(a * v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu =
0.16
*
Re^0.699
... [2.5e3<Re<8e3]
Nu = 0.092 * Re^0.675 ... [5e3<Re<1e5]
08c. Umströmung eines
Rohres - Rechteck (a,b):
[Tdef
= (T+Ts)/2, 2.5e3<Re<1e5, 0.5<Pr<1e3,
0.5<a/b<1] ...
(Principles of Heat Transfer
7th. edtion)
Dh =2
* (a + b) / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu = 0.104 *
Pr^0.35 *
Re^0.675
..... [a/b=1]
Nu
= 0.264
* Pr^0.35 *
Re^0.66
...... [a/b=0.5]
Re-Nu-hc Graph für Luft und Wasser (T ... [°C], D,Dh,L ... [mm])
09a.
Umströmung eines Rohres - Quadrat (a):
[Tdef = (T+Ts)/2, 5e3<Re<1e5,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =4 * a / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ) / Dh
* fcoeff
Nu =1.11 *
0.222 * Re^0.588 * Pr^0.31
Nu =1.11 * 0.222 * Re^0.588
* Pr^0.31 * (0.785 * (Ts/T)^(0.588/4) ..... for Gas
09b.
Umströmung eines Rohres - Quadrat (a):
[Tdef = T, 2.5e3<Re<1e5,
0.6<Pr<0.85] ...
(Principles of Heat Transfer
7th. edtion)
x = (2 *
a^2)^0.5
Re =(x *
v) / KinVis
hc = (Nu *
λ)
/ x
* fcoeff
Nu =
0.261*
Re^0.624 ... [2.5e3<Re<7.5e3]
Nu = 0.222 * Re^0.588 ... [5e3<Re<1e5]
10a. Umströmung eines
Rohres - Sechseck (a):
[Tdef = (T+Ts)/2, 5e3<Re<1e5,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =6 * a / (3^0.5) / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ) / Dh
* fcoeff
Nu =1.11 *
0.138 * Re^0.638 * Pr^0.31
Nu =1.11 * 0.138 * Re^0.638
* Pr^0.31 * (0.785 * (Ts/T)^(0.638/4) ..... for Gas
10b. Umströmung eines Rohres -
Sechseck (a):
[Tdef = (T+Ts)/2,
5e3<Re<1e5,
0.6<Pr<0.85] ... (Principles of Heat
Transfer
7th. edtion)
Re =(a *
v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu = 0.138 * Re^0.638
11a.
Umströmung eines Rohres - Sechseck (a):
[Tdef = (T+Ts)/2, 5e3<Re<1.95e4,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =6 * a / (3^0.5) / 3.14
Re = (Dh * v) / KinVis
hc = (Nu * λ) / Dh
* fcoeff
Nu =1.11 *
0.144
* Re^0.638 * Pr^0.31
Nu =1.11 * 0.144 * Re^0.638
* Pr^0.31 * (0.785 * (Ts/T)^(0.638/4) ..... for Gas
11b.
Umströmung eines Rohres - Sechseck (a):
[Tdef = (T+Ts)/2, 5e3<Re<1e5, ,
0.6<Pr<0.85] ... (Principles of Heat
Transfer
7th. edtion)
x = 2 * a /
(3^0.5)
Re =(x *
v) / KinVis
hc = (Nu *
λ)
/ x
* fcoeff
Nu =
0.144
*
Re^0.638 ... [5e3<Re<1.95e4]
Nu = 0.035 * Re^0.782 ... [1.95e4<Re<1e5]
12.
Kugelumströmung (D):
[Tdef = T, 3.5<Re<2e5,
0.7<Pr<380] ... (Principles
of Heat Transfer
7th. edtion)
hc = (Nu *
λ)
/ D * fcoeff
Nu =2 + (0.4 *
Re^0.5 + 0.06 * Re^(0.67)) * Pr^0.4 * (μ
/ μs)^0.25 ...
[3.5<Re<76000]
Nu =2 + (Re / 4 + 0.0003 *Re2^1.6)^0.5 ... [76000<Re<2e5]
13.
Platteumströmung φ=90° (a): [Tdef
= (T+Ts)/2, Re<1e7, 0.6<Pr<60]
... (Heat
Transfer Applications for the Practicing Engineer)
Re =(a *
v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu =
0.644
*
Re^0.5 *
Pr^0.333
... [Re<5e5,
0.6<Pr<50]
Nu = 0.037 * Re^0.8 * Pr^0.333 ... [5e5<Re<1e7,
0.6<Pr<60]
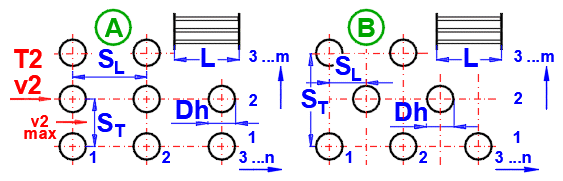
A.
Rohrbündelumströmung
(D,
ST, SL, n): [Tdef = (T+Ts)/2, 0.7<Pr<500, 10<Re<200000]
...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D * A
Nu = 0.8 * Re^0.4 * Pr^0.36 * (Pr/Prs)^0.25 [10<Re<1000]
Nu = 0.27 * Re^0.63 * Pr^0.36 * (Pr/Prs)^0.25 [1000<Re<2e5, ST/SL>0.7]
Nu = 0.021 * Re^0.84 * Pr^0.36 * (Pr/Prs)^0.25 [2e5<Re]
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Coeff A |
0.68 |
0.75 |
0.83 |
0.89 |
0.92 |
0.95 |
0.97 |
0.98 |
0.99 |
1.00 |
|
Coeff B |
0.64 |
0.80 |
0.87 |
0.90 |
0.92 |
0.94 |
0.96 |
0.98 |
0.99 |
1.00 |
B.
Rohrbündelumströmung (D,
ST, SL, n): [Tdef = (T+Ts)/2, 0.7<Pr<500, 10<Re<200000]
...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D * B
Nu = 0.9 * Re^0.4 * Pr^0.36 * (Pr/Prs)^0.25 [10<Re<1000]
Nu = 0.35 * (ST/SL)^0.2 * Re^0.6 * Pr^0.36 * (Pr/Prs)^0.25 [(ST/SL)<2,
1000<Re<2e5]
Nu = 0.4 * Re^0.6 * Pr^0.36 * (Pr/Prs)^0.25 [(ST/SL)>2, 1000<Re<2e5]
Nu = 0.022 * Re^0.84 * Pr^0.36 * (Pr/Prs)^0.25 [Pr>1, 2e5<Re]
Nu = 0.019 * Re^0.84 [Pr=0.7, 2e5<Re]
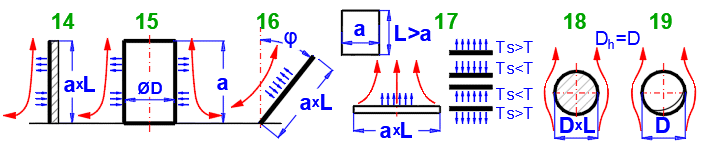
14-15. Vertikale Platte
oder vertikaler Zylinder
(L): [Tdef = (T+Ts)/2, 1e3 < Ra < 1e13]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ L
Nu = 0.59 * Ra^0.25
[1e4<Ra<1e9]
Nu = 0.10 * Ra^0.333 [1e9<Ra<1e13]
16. Geneigte Platte
(L):
[0°<φ<89.9°, Tdef = (T+Ts)/2, 1e3 < Ra < 1e13]
...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ)
/ L
Nu = 0.59 * (Ra*cos(φ))^0.25
[1e4<Ra<1e9]
Nu = 0.10 * (Ra*cos(φ))^0.333
[1e9<Ra<1e13]
17. Platte - Oberseite
(kleinere Abmessung AxB):
[Tdef = (T+Ts)/2, 2e4 < Ra < 1e11]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ L
Ts > T
Nu = 0.54 * Ra^0.25 [2e4 < Ra < 8e6]
Nu = 0.15 * Ra^0.333 [8e6 < Ra < 1e11]
Ts < T
Nu = 0.58 * Ra^0.2 [8e6 < Ra < 1e11]
17. Platte - Unterseite
(kleinere Abmessung AxB):
[Tdef = (T+Ts)/2, 2e4 < Ra < 1e11]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ L
Ts < T
Nu = 0.54 * Ra^0.25 [2e4 < Ra < 8e6]
Nu = 0.15 * Ra^0.333 [8e6 < Ra < 1e11]
Ts > T
Nu = 0.58 * Ra^0.2 [8e6 < Ra < 1e11]
18. Horizontaler Zylinder (D): [Tdef
= (T+Ts)/2, 1e-5 < Ra < 1e12] ...
(Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ D
Nu = 0.4 * Ra^0 [0 < Ra < 1e-5]
Nu = 0.85 * Ra^0.188 [1e-5 < Ra < 1e4]
Nu = 0.53 * Ra^0.25 [1e4 < Ra < 1e9]
Nu = 0.13 * Ra^0.333 [1e9 < Ra < 1e12]
19. Kugel (D): [Tdef = (T+Ts)/2, 1e-5 < Ra < 1e12]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ D
Nu1=0.6 * Ra^0.25
Nu2=2 + (0.589 * Ra^0.25) / (1 + (0.469 / Gr^(9/16)))^(4/9)
Nu=(Nu1 + Nu2) / 2
Die Berippung wird zur Erhöhung des Wärmeübergangs (Vergrößerung der Wärmeübertragungsfläche) in verschiedenen Anwendungen wie Computer-Kühlkörpern, Heizsystemen und Wärmetauschern eingesetzt. Die einfachste (und annähernde) Berechnungsmethode berücksichtigt lediglich die gesamte Oberfläche der berippten Fläche und den Wärmeübergangskoeffizienten hc, der sich auf die unberippte Oberfläche bezieht.
Die in dieser Berechnung verwendeten Gleichungen berücksichtigen auch andere Parameter wie Rippenform und -abmessungen.
Das Ergebnis der Rippenberechnung ist
die gesamte Wärmeübertragungsfläche At und der Gesamtwirkungsgrad der Berippung
ηof.
Die modifizierte Gleichung zur Berechnung des spezifischen konvektiven
Wärmestroms qc′ lautet:
qc' = hc * (T - Ts) * ηof
Und zur Berechnung des gesamten konvektiven Wärmestroms Qc lautet die Gleichung:
Qc = qc' * At
Die in dieser Anwendung behandelten Rippenformen und Strömungsbedingungen um die Rippen sind unten beschrieben.
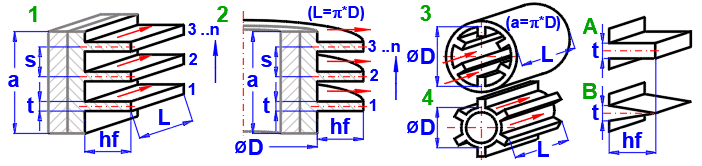
1A) Gerade Rippen - Rechteckig
Af = 2 * hfc * L [m²]
hfc = hf + (t/2) [m]
Ap = t * hf [m²]
1B) Gerade Rippen - Dreieckig
Af = 2 * L * (hf^2 + (t/2)^2)^0.5 [m²]
Ap = (t /2) * hf
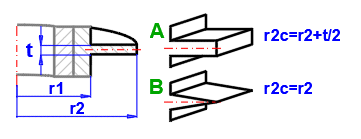
2A) Ringrippen - Rechteckig
Af = (3.1416 * (D/2 + hfc)^2 - 3.1416 * (D/2)^2) * 2
hfc = hf + (t/2) [m]
Ap = t * hf [m²]
2B) Ringrippen - Dreieckig
Af = (3.1416 * (D/2 + hfc)^2 - 3.1416 * (D/2)^2) * 2
hfc = (hf^2 + (t / 2.3)^2)^0.5)
Ap = (t /2) * hf
Wobei:
Af ... Rippenfläche
hf ... Rippenhöhe
hfc ... Korrigierte Rippenhöhe
Ap ... Rippenquerschnittsfläche
Die x-Koordinate des Diagramms ist ein
dimensionsloser Wert:
x = hfc^(3/2) * (hc / (Lambda * Ap))^(1/2)
Wobei:
hc ... Wärmeübergangskoeffizient [W/m²K]
Lambda ... Wärmeleitfähigkeit des Rippenmaterials [W/(m.K)]
Die y-Koordinate des Diagramms ist der Rippenwirkungsgrad ηf.
Wirkungsgrad gerader Rippen mit rechteckigem, dreieckigem und parabolischem Profil
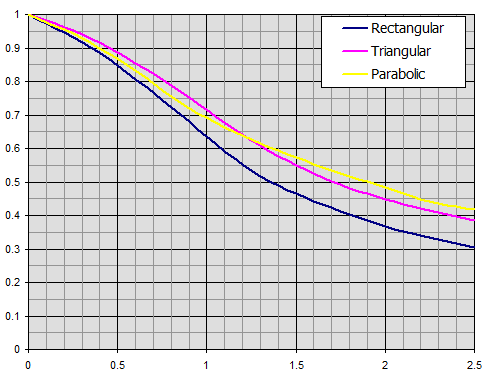
Wirkungsgrad von Ringrippen mit konstanter Dicke t
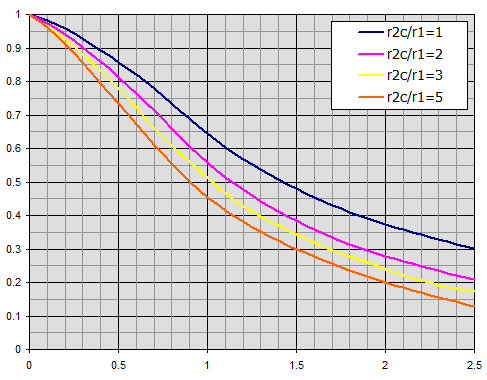
Einzelne Kurven beziehen sich auf das Radienverhältnis r2c/r1.
ηof = (1 - (n * Af) / At * (1 - ηf))
Wobei:
n ... Anzahl der Rippen
Af ... Rippenfläche
At ... Gesamtfläche
ηf ... Rippenwirkungsgrad
Strahlungsenergie wird durch elektromagnetische Strahlung unterschiedlicher Wellenlänge übertragen. Die Problematik der Wärmeübertragung durch Strahlung ist relativ komplex, daher werden nur grundlegende Aufgaben behandelt, die in der gängigen Maschinenbaupraxis Anwendung finden.

In den Formeln wird die Kennzeichnung gemäß Abbildung verwendet.
hr = ɛ * δ0 * (Ts^4 - Tsky^4) / (Ts - Tsky)
Dabei gilt:
ε ... Emissionsgrad der Wand [0...1]
δ0 ... Stefan-Boltzmann-Konstante, δ0=δ0
= 5.67e-8 [W/m²/K⁴]
Ts ... Wandtemperatur [°K]
Tsky ... Raumtemperatur [°K]
Q1 = ε1 * δ0 * A1 * (T1K^4 - Tsky^4)
Dabei gilt:
ε1 ... Emissionsgrad der Wand [0...1]
δ0 ... Stefan-Boltzmann-Konstante, δ0=δ0
= 5.67e-8 [W/m²/K⁴]
Tsky ... Raumtemperatur [°K]
T1K ... Wandtemperatur [°K]
q1 = Q1 / A1
A1 ... Wandfläche [m²]
Q12 = (δ0 * A1 * (T1K^4 - T2K^4)) / (1/ε1 + A1/A2 * (1/ε2 - 1))
Dabei gilt:
ε1 ... Emissionsgrad der Wand 1 [0...1]
ε2 ... Emissionsgrad der Wand 2 [0...1]
A1 ... Fläche der Wand 1 [m²]
A2 ... Fläche der Wand 2 [m²]
T1K ... Temperatur der Wand 1 [°K]
T2K ... Temperatur der Wand 2 [°K]
q12 = Q12 / A1
A1 ... Fläche der Wand 1 [m²]
Q12 =(δ0 * (T1K^4 - T2K^4)) / ((1 - ε1) / (ε1 * A1) + (1 - ε3) / (ε3 * Ax) + (1 - ε4) / (ε4 * Ax) + (1 - ε2) / (ε2 * A2))
Dabei gilt:
ε3 ... Emissionsgrad der Abschirmfolie x [0...1]
ε4 ... Emissionsgrad der Abschirmfolie x [0...1]
Ax ... Fläche der Abschirmfolie x [m²]
q12 = Q12 / A1
A1 ... Fläche der Wand 1 [m²]
Tx = ((R1 * T2K^4 + R2 * T1K^4) / (R1 + R2))^0.25
R1 ... Widerstand zwischen 1 und x
R2 ... Widerstand zwischen x und 2
R1 = (1 - ε1) / (ε1 * A1) + (1-ε3) / (ε3 * Ax)
R2 = (1 - ε4) / (ε4 * Ax) + (1 - ε2) / (ε2 * A2)
Q12 = (δ0 * (T1K^4 - T2K^4)) / Rsum
Rsum = R1 + R2 + R3
R1 = (1 - ε1) / (ε1 * A1) + (1 - ε3) / (ε3 * Ax)
R2 = (1 - ε4) / (ε4 * Ax) + (1 - ε5) / (ε5 * Ay)
R3 =(1 - ε6) / (ε6 * Ay) + (1 - ε2) / (ε2 * A2)
R1 ... Widerstand zwischen 1 und x
R2 ... Widerstand zwischen x und y
R3 ... Widerstand zwischen y und 2
q12 = Q12 / A1
A1 ... Fläche der Wand 1 [m²]
Tx = (T1K^4 - Q12 * R1 / δ0)^0.25
Ty = (T2K^4 + Q12 * R3 / δ0)^0.25
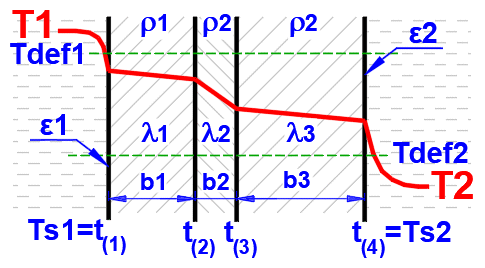
Die Berechnung des komplexen Wärmestroms ist nicht einfach und direkt lösbar. Der Wärmestrom hängt von einer Vielzahl von Parametern ab (Temperaturen, Flüssigkeitseigenschaften, Wandmaterial, Geometrie usw.), die sich mit der Wandtemperatur ändern.
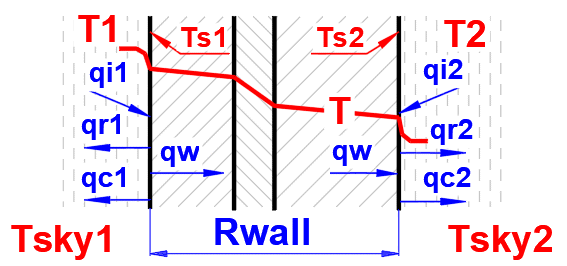
Zur Bestimmung der
Wandtemperaturen Ts1 und Ts2 wird die Wärmestromgleichung für die vorgegebenen
Flüssigkeits- und Wandparameter verwendet. Die Temperaturen Ts1 und Ts2 werden
schrittweise verfeinert, um die folgenden Gleichungen zu erfüllen:
Ts2 = Ts1 - q1 * Rwall, Q1 = -Q2
Q1 = (qi1 + qr1 + qc1) * A1
Q2 = (qi2 + qr2 + qc2) * A2
Q1 ... Gesamtwärmestrom der linken
Seite [W]
Q2 ... Gesamtwärmestrom der rechten Seite [W]
Für die
Berechnung des Wärmestroms q werden die folgenden Beziehungen (siehe vorherige
Abschnitte) verwendet:
qc = hc * (T - Ts) ... f (T, Ts, p, Rho, μ, Cp, λ.....)
qr = hr * (T - Ts) ... f (T, Ts, ε.....)
qi ... Eingabeparameter - direkte
Bestrahlung (Sonne, externe Wärmequelle usw.)
Die Lösung für die Wandtemperaturen Ts1 und Ts2 führt selbstverständlich dazu, dass sich die Werte für hc1, hc2, hr1 und hr2 ändern. Daher kann eine zweite Iteration manuell gestartet werden, bei der neue Werte für hc1 und hc2 wiederholt verwendet werden, um die Ergebnisse weiter zu präzisieren.
Lösung für die Temperaturen Ts1 und Ts2:
Erster Schätzwert
(n=1):
Ts1K[°K] = 100
*
(ABS((T1K
/
100)^4 - qi1
/ c0'))^0.25
Ts2K[°K] =
Ts1K - q1 * Rwall
qc1[W/m²] =
(T1K
-
Ts1K)
*
hc1
*
FinEff1
qc2[W/m²] = (Ts2K - T2K) * hc2
*
FinEff2
qr1[W/m²] =
(Tsky1
-
Ts1K)
*
hr1
qr2[W/m²] = (Ts2K - Tsky2) * hr2
q1[W/m²] = qi1 + qc1 + qr1
q2[W/m²] = qi2 + qc2 + qr2
ΔQ[W] =
Q1
-
Q2 = (q1 * A1 - q2 * A2) /
A2
ΔTs2 =IF(ABS(ΔQ)
> 1;(ΔQ/ABS(ΔQ)*(ABS(ΔQ)^0.5));ΔQ/2)
Approximation (100 Schritte,
Halbintervallmethode, n=2…100):
Ts1K(n) = Ts1K(n-1) + ΔTs2(n-1)
Ts2K(n) = Ts1K(n) - q1 * Rwall
qc1(n) = (T1K
-
Ts1K(n))
*
hc1
*
FinEff1
qc2(n) = (Ts2K(n) - T2K) * hc2
*
FinEff2
qr1 =
(Tsky1
-
Ts1K(n))
*
hr1
qr2 = (Ts2K(n) - Tsky2) *
hr2
qw(n) =
1
/
Rwall
*
(Ts2K(n)
- Ts1K(n))
q1(n) = qi1 + qc1(n) + qr1(n)
q2(n) = qi2 + qc2(n) + qr2(n)
ΔQ(n) =
Q1(n)
-
Q2(n) = (q1(n) * A1 - q2(n)
* A2) / A2
ΔTs2(n) = IF(ΔQ(n-1)*ΔQ(n) < 0; ΔTs2(n-1)/-2; ΔTs2(n-1))
Wobei:
c0′=δ0 * 1e8=5.67
δ0=5.67e-8 ... Stefan-Boltzmann-Konstante
[W/m²/K⁴]
RWand ... Thermischer Widerstand der Wand
[m²K/W]
Tsky
... Umgebungstemperatur [K]
FinEff ... Rippenwirkungsgrad [0 ... 1]
Zur genauen Bestimmung der länglichen Temperaturänderung in einer Rohrleitung mit strömendem Medium (Flüssigkeit, Gas) gilt folgende Gleichung:
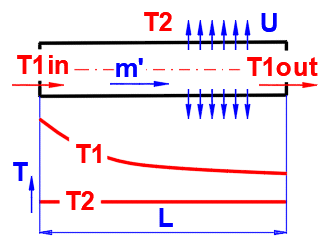
dTL = ABS(T1in - T2) * EXP(-Alpha * L)
T1in ...
Eintrittstemperatur des Mediums [°C]
T2 ... Umgebungstemperatur [°C]
L ... Abstand vom Eintritt [m]
Alpha = U / (m' * Cp)
U ... Linearer
Wärmeübergangskoeffizient [W/m/K]
m′ ... Massenstrom des Mediums [kg/s]
Cp ... Spezifische Wärmekapazität des Mediums [J/kg/K]
T1out =
T2 + dTL ...
(T1in>T2)
T1out = T2 - dTL .... (T1in<T2)
T1out ... Austrittstemperatur (Temperatur in Entfernung L vom Eintritt) [°C]
Leistung / Wärmeleistung
Pw = -m' * Cp * (T1in - T1out) [W]
Die Berechnung der Abkühlzeit berücksichtigt keine Phasenänderungen des Stoffes.
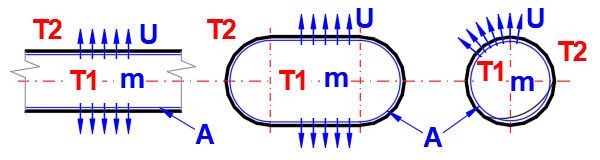
Phi = U * A * (1Ts - T2)
U ... Flächenbezogener
Wärmeübergangskoeffizient [W/m²/K]
A ... Innere Oberfläche des Rohres, Behälters [m²]
T1s ... Anfangstemperatur des Mediums im Inneren [°C]
T2 ... Umgebungstemperatur [°C]
Time = ((T1s - T2) * m * Cp * LN((T1s - T2) / (T1e - T2)) / Phi
m ... Masse des Mediums
[kg]
Cp ... Spezifische Wärmekapazität des Mediums [J/kg/K]
T1e ... Endtemperatur des Mediums im Inneren [°C]
Grundtypen von Wärmetauschern
- Gleichstrom-Wärmetauscher
- Gegenstrom-Wärmetauscher
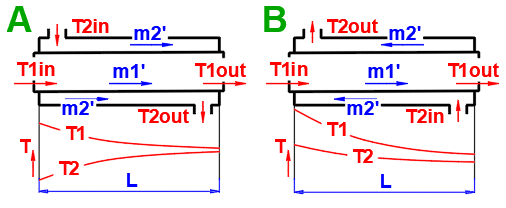
Abgeleitete Wärmetauschertypen
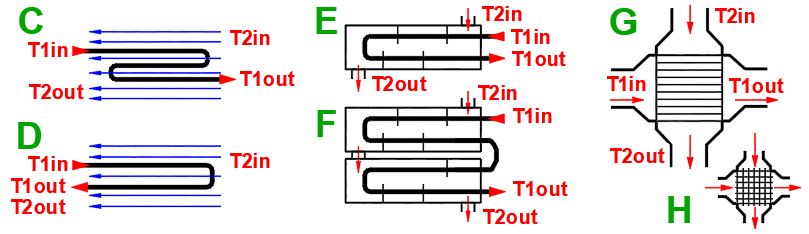
Q1 = m1'
*
Cp1
*
dT1
Q2 = m2'
*
Cp2
*
dT2
Wobei:
m˙1,m˙2 ... Massenstrom [kg/s]
Cp1,Cp2 ... Spezifische Wärmekapazität [J/(kg·K)]
ΔT1,ΔT2 ... Temperaturdifferenz [°C]
Gleichstrom-Wärmetauscher
Gegenstrom-Wärmetauscher
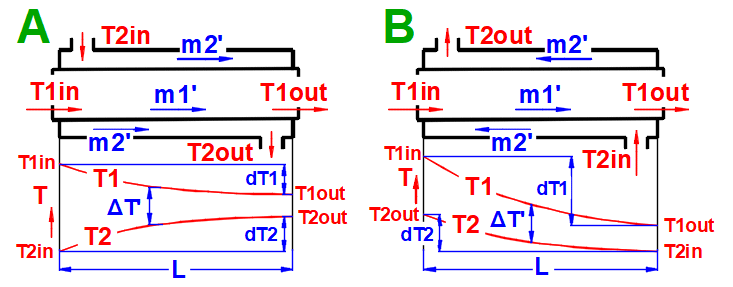
dT1 = T1Kout - T1Kin [°C]
dT2 = T2Kout - T2Kin [°C]
Gleichstrom A:
ΔTS' = ((T1Kin - T2Kin) - (T1Kout - T2Kout)) / (LN((T1Kin
- T2Kin) / (T1Kout - T2Kout)))
Gegenstrom B:
ΔTP' = ((T1Kin - T2Kout) - (T1Kout - T2Kin)) /
(LN((T1Kin - T2Kout) / (T1Kout - T2Kin)))
Wärmetauscher Typ C-H: ΔTX' = ΔTP' * Epsilon
Wobei:
T1Kin, T2Kin ... Eintrittstemperatur des Fluids [°K]
T1Kout, T2Kout ... Austrittstemperatur des Fluids [°K]
Epsilon ... Korrekturfaktor für die logarithmische mittlere Temperaturdifferenz [0.5 -
1.0]
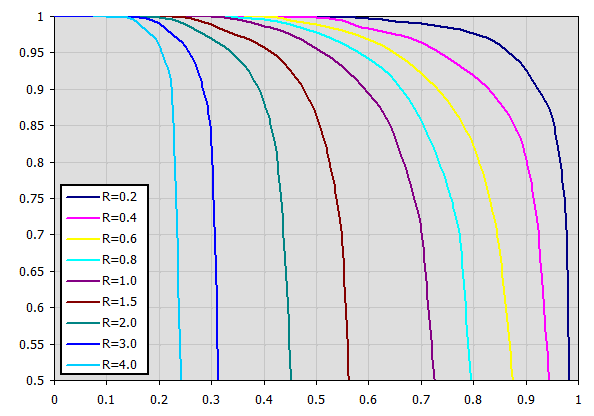
Der Korrekturfaktor wird aus Tabellen mittels linearer Interpolation für Wärmetauscher vom Typ C-H approximiert.
Wärmekapazitätsverhältnis R
R = (T1Kin - T1Kout) / (T2Kout - T2Kin)
Temperatureffektivität P
P = (T2Kout - T2Kin) / (T1Kin - T2Kin)
Entsprechende Diagramme für Epsilon für viele Wärmetauschertypen sind in der zitierten Literatur verfügbar.
Beispiel-Diagramm (Tabellenapproximation) für Wärmetauscher Typ F: (XAchse ... P, YAchse ... Epsilon) Für P=0.7, R=0.8 => Epsilon=0.85
A = ABS(Q1 / (Upl * ΔT'))
Wobei:
Q1,Q2 ... Wärmestrom [W], Bedingung: Q1=−Q2
ΔT′ ... Logarithmische mittlere Temperaturdifferenz (ΔTS′,ΔTP′,ΔTX′) [°C]
Upl ... Gesamtwärmedurchgangskoeffizient - ebene Wand [W/m²/K]
L = ABS(Q1 / (Ucyl * ΔT'))
Q1,Q2 ... Wärmestrom [W], Bedingung:
Q1=−Q2
ΔT' ... Logarithmische mittlere Temperaturdifferenz (ΔTS',
ΔTP', ΔTX') [°C]
Ucyl ...
Gesamtwärmedurchgangskoeffizient - zylindrische Wand [W/m/K]
Gleichstrom A: T1Out = T1in - Theta1S
Gegenstrom B: T1Out = T1in - Theta1P
Wärmetauscher Typ C-H:
T1Out =
T1in - Theta1X
Gleichstrom A: T2Out = T2in + Theta2S
Gegenstrom B: T2Out = T2in + Theta2P
Wärmetauscher Typ C-H:
T2Out =
T2in - Theta2X
Theta1S = (T1Kin - T2Kin) * FiS
Theta1P = (T1Kin - T2Kin) * FiP
Theta1X = (T1Kin - T2Kin) * FiX
Theta2S = C1 / C2 * Theta1S
Theta2P = C1 / C2 * Theta1P
Theta2X = C1 / C2 * Theta1X
C1 = m1'
*
Cp1
C2 = m2'
*
Cp2
Gleichstrom A: FiS = (1 - EXP(-U * OmegaS * LA)) / (1 + C1/C2)
Gegenstrom B: FiP = (1 - EXP(-U * OmegaP * LA)) / (1 - C1/C2 * EXP(-U * OmegaP *
LA))
Wärmetauscher Typ C-H:
FiX =
(1 -
EXP(-U * OmegaX * LA)) / (1 - C1/C2 * EXP(-U * OmegaX * LA))
LA = Areq / (1 / Epsilon)
Wobei:
Areq ... Angegebene Fläche, für die die Austrittstemperatur ermittelt werden
soll [m²]
Epsilon
... Korrekturfaktor für die logarithmische mittlere Temperaturdifferenz
(Wärmetauscher Typ C-H) [0.5 - 1.0]
U ... Gesamtwärmedurchgangskoeffizient - ebene Wand [W/m²/K]
Gleichstrom A: OmegaS = 1/C1 + 1/C2
Gegenstrom B:
OmegaP =1/C1 - 1/C2
Wärmetauscher Typ C-H: OmegaX =1/C1 - 1/C2
Rf = 1/Ud - 1/Uc
Ud = 1/ (Rf + 1/Uc)
Wobei:
Rf ... Verschmutzungsfaktor [m²K/W]
Uc ... Gesamtwärmedurchgangskoeffizient der sauberen Fläche [W/m²/K]
Eine Vielzahl von technischen (Bau-)Konstruktionen ist der Sonneneinstrahlung ausgesetzt. Die Berechnung dient zur Bestimmung des solaren Wärmestroms pro Fläche für vorgegebene Bedingungen (Ausrichtung der Fläche, Datum, Stunde, Höhe über dem Meeresspiegel, Verschmutzung) und zur Bestimmung der gesamten täglichen Energiezufuhr.
Verwendete Beziehungen
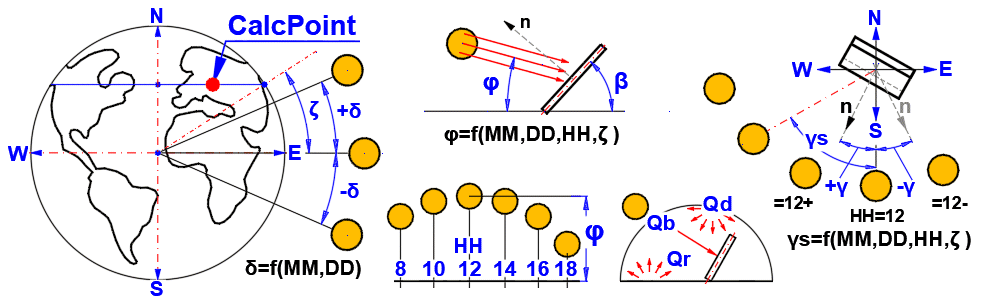
Winkel:
δ = 23.45 * SIN((360 * (284 + nn) / 365) * PI()/180)
nn ... Fortlaufender Tag im Jahr (1-365)
φ = ASIN((SIN(Latitude*PI()/180) * SIN(δ*PI()/180)) + (COS(Latitude*PI()/180) * COS(δ*PI()/180) * COS(15*PI()/180*(HH-12))))*180/PI()
Latitude ... Geografische Breite [deg]
HH ... Stunde [0-24]
γs = ASIN(COS(δ*PI()/180) / COS(φ*PI()/180) * SIN(Tau*PI()/180))*180/PI()
Tau = 15 * (HH-12) ... Solarer Stundenwinkel [deg] (vormittags (-), nachmittags (+))
θ = ACOS((SIN(φ*PI()/180) * COS(β*PI()/180) + COS(φ*PI()/180) * SIN(β*PI()/180) * COS((γs - γ)*PI()/180)))*180/PI()
β ... Neigung der Fläche (0-90) [deg]
γ ... Azimut der Fläche (+-180) [deg]
Strahlungsleistung:
Qon =SolarConst * (1 + 0.033 * COS((360*nn/365)*PI()/180))
Der solare Strahlungsfluss außerhalb der
Atmosphäre ändert sich im Laufe des Jahres um ±3.3% (Abstand Erde-Sonne).
SolarConst ... Solarkonstante (Mittelwert 1367W/m²)
Qbn = Qon * EXP( -(Zcoeff / EpsilonCoeff))
Zcoeff ... Koeffizient der atmosphärischen Verschmutzung (1.5 -6)
EpsilonCoeff = (9.38076 * (SIN(φ*PI()/180) + (0.003 + SIN(φ*PI()/180)^2)^0.5)) /
(2.0015 * (1-Lv*10^-4))+0.91018
Lv ... Höhe über dem Meeresspiegel [m]
QbT = Qbn * COS(θ*PI()/180)
Qd = 0.33 * (Qon - Qbn) * SIN(φ*PI()/180)
QdT = ((1+COS(β*PI()/180))/2) * Qd
QrT = Rhog * ((1 - COS(β*PI()/180))/2) * (Qb + Qd)
Qb = QbT * SIN(φ*PI()/180) / COS(θ*PI()/180)
Rhog ... Verhältnis zwischen reflektierter und einfallender solarer
Strahlungsflussdichte
(0-1).
QT' = QbT + QdT + QrT
QT = As * QT'
As ... Gesamte bestrahlte Fläche
Q = QT * Efficiency / 100
Efficiency ... Wirkungsgrad der Umwandlung von Sonneneinstrahlung in nutzbare Energie (0-100).
Zur Berechnung von Pw wird der Wert von Q in Schritten von 30 Minuten für t=0−24h ermittelt. Diese Werte werden dann zur Gesamt-Pw summiert.
Pw = Sum (Q(t) * 0.5) [t=0-24]
Berechnungsprozess Die hier bereitgestellten Berechnungen decken häufig auftretende Probleme im Bereich der Thermomechanik ab. Da diese Probleme nur lose miteinander verbunden sind, wird hier kein universelles Verfahren beschrieben. Die Vorgehensweisen variieren je nach dem spezifischen Problem. Wenn Ihre Aufgabe in den Anwendungsbereich der behandelten Probleme fällt, empfehlen wir Ihnen, die in der Hilfe-Dokumentation bereitgestellten Beispiele zu überprüfen. Für jeden Berechnungstyp sind in der Regel mehrere typische Beispiele enthalten, um Sie mit dem spezifischen Verfahren vertraut zu machen.
In diesem Absatz werden die Einheiten der Berechnung eingestellt.
In einer Auswahlliste das benötigte Einheitssystem der Berechnung wählen. Beim Umschalten der Einheiten werden sofort alle Eingangswerte umgerechnet.
In das Eingabefeld auf der linken Seite geben Sie den Wert ein, den Sie übertragen wollen. Verdoppeln Sie die Quelleneinheiten und auf der rechten Seite wählen Sie die Zieleinheiten.
Dieser Abschnitt behandelt grundlegende Energieberechnungen, einschließlich Erwärmung, Kühlung, Phasenwechsel und Verbrennung. Sofern nicht anders angegeben, sind die Koeffizienten in den Tabellen für eine Temperatur von 20 C und einen Druck von 0.1 MPa angegeben.
Energie muss zugeführt oder abgeführt werden, um eine Substanz zu erwärmen oder zu kühlen.
Wählen Sie die Materialgruppe. Der Zeiger in der Materialtabelle (nächste Zeile) wird auf das erste Material des entsprechenden Typs gesetzt.
Wählen Sie das Material.
Dies sind Informationswerte und haben keinen Einfluss auf die Berechnung.
Der Wert von Cp für das ausgewählte Material wird im grünen Feld angezeigt. Sie können Ihren eigenen Wert eingeben, indem Sie die Schaltfläche deaktivieren.
Geben Sie die Masse des zu erwärmenden oder zu kühlenden Materials ein. Der Schalter auf der rechten Seite bestimmt, welcher Wert berechnet werden soll.
Geben Sie die Temperaturänderung ein.
Die für die Temperaturänderung aufgewendete Energie.
Energie muss bei einem Phasenwechsel (Feststoff → Flüssigkeit → Gas) zugeführt oder abgeführt werden.
Wählen Sie das Material. Die Schmelztemperatur [TM] und die Siedetemperatur [TB] sind in eckigen Klammern angegeben.
Die Werte für CpM und CpB des aus der Liste ausgewählten Materials befinden sich im grünen Feld. Sie können Ihre eigenen Werte eingeben, indem Sie die Schaltfläche deaktivieren.
Geben Sie die Masse des Mediums ein. Wenn das Kontrollkästchen aktiviert ist, wird der Wert aus der vorherigen Berechnung verwendet.
Die beim Phasenwechsel aufgewendete oder gewonnene Energie.
Die Verbrennungswärme
(Higher Heating Value - HHV) ist die Wärmemenge, die bei der isobaren Verbrennung von 1 Mol einer Verbindung in gasförmigem Sauerstoff zu den endgültigen Oxidationsprodukten freigesetzt wird. Es wird angenommen, dass das bei der Verbrennung freigesetzte Wasser kondensiert und die chemische Reaktionsenergie nicht um ihre latente Wärme reduziert werden muss.
Der Brennwert
(Lower Heating Value - LHV) geht davon aus, dass Wasser am Ende der Reaktion in gasförmigem Zustand vorliegt.
Daher ist der HHV-Wert immer größer oder gleich dem LHV-Wert. Gleichheit tritt auf, wenn bei der Verbrennung kein Wasser entsteht.
Wählen Sie das verbrannte Material aus der Liste.
Für den Brennwert (Lower Heating Value - LHV) wird angenommen, dass Wasser am Ende der Reaktion in gasförmigem Zustand vorliegt.
Der Wert der Verbrennungswärme (HHV) ist genau für die Verbrennung definierter Verbindungen (H2, CH4O, etc.).
Für Brennstoffe, die verschiedene Gemische enthalten (Kohle, Erdölprodukte, Erdgas etc.), können die typischen Werte niedriger oder höher sein als der Tabellenwert. Die geschätzte Abweichung von den Tabellenwerten ist im grünen Feld angegeben. Sie können Ihren eigenen HHV-Wert eingeben, indem Sie die Schaltfläche deaktivieren.
Geben Sie die Masse des verbrannten Materials ein.
Die Verbrennungseffizienz gibt an, wie viel Energie aus dem Brennstoff auf das Wärmeträgermedium übertragen wird.
Gaskessel:
Brennwertkessel: bis zu 98%
Niedertemperaturkessel: bis zu 89%
Konventionelle Kessel: bis zu 84%
Festbrennstoffkessel:
Holz- oder Holzpellet-Vergaserheizkessel: bis zu 92%
Automatische Kohlekessel: 80% bis 90%
Kohle- und andere Festbrennstoffkessel: über 70%
Die aus der Kraftstoffverbrennung gewonnene Energie.
Dieser Abschnitt behandelt das Periodensystem der Elemente, die Berechnung der Molmasse und der Poisson-Konstante für Elemente, Verbindungen und deren Gemische. Der zweite Teil berechnet den Zustand und die Zustandsänderung eines idealen Gases (pV=mrT).
Geben Sie die chemische Summenformel der Verbindung ein. Nach dem Drücken der Taste ">>" wird die Formel in einzelne Elemente zerlegt und die entsprechende Liste unten ausgefüllt. Wenn Sie ein Gemisch von Verbindungen lösen möchten, trennen Sie diese durch ein "+"-Zeichen. Beim Lesen der Formel wird die fortlaufende Nummer der Verbindung (des Elements) im Gemisch in der letzten Spalte der Tabelle ergänzt.
Beispiele für Verbindungen: h2so4, H2O, cO2, C4H10O, C2H3ClO2
Beispiele für Gemische:
Luft: N2+O2+Ar+CO2
Alkohol(40%)+Wasser(60%): C2H5OH+H2O
Die Tasten "1-20", "21-40"... füllen die Tabelle mit den entsprechenden Elementen.
Die Parameter des aus der Liste ausgewählten Elements werden in der entsprechenden Zeile angezeigt. Die Taste "Clear" löscht die Zeilen 2-20.
Elementsymbol.
Anzahl der Atome.
Atomgewicht.
Molgewicht.
Dichte des Elements.
Spezifische Wärmekapazität.
Spezifische Wärmekapazität beim Schmelzen (Schmelzwärme).
Spezifische Wärmekapazität beim Sieden (Verdampfungswärme).
Wärmeleitfähigkeit.
Schmelztemperatur.
Siedetemperatur.
Fortlaufende Nummer der Verbindung. Für die weitere Berechnung der Gemischparameter ist es notwendig, die fortlaufende Nummer der Verbindung zu bestimmen. Einzelne Elemente in der Verbindung müssen daher die gleiche fortlaufende Nummer haben.
In der vorherigen Tabelle können Sie einzelne Elemente und Verbindungen, gekennzeichnet durch eine fortlaufende Nummer, definieren.
In dieser Tabelle können Sie dann nach Eingabe des Massenanteils im Gemisch die gesamte Molmasse des Gemisches bestimmen.
Für ideale Gase wird die Poisson-Konstante aus der Anzahl der Freiheitsgrade des jeweiligen Moleküls bestimmt.
Molmasse des einzelnen Elements oder der Verbindung.
Geben Sie den Massenanteil der einzelnen Gemischkomponenten ein. Wenn die Schaltfläche rechts aktiviert ist, bleiben die ursprünglichen Werte beim Ausfüllen des Gemisches aus der Formel [3.2] erhalten. Wenn die Schaltfläche deaktiviert ist, wird jeder Komponente des Gemisches der gleiche Wert zugewiesen.
Die rote Summenzelle am Ende der Zeile weist darauf hin, dass die Summe nicht 100% beträgt.
Molmasse des Gemisches.
r = R / Msum
R ... Universelle Gaskonstante (8314.46261815324 J/kmol/K)
Msum ... Molmasse des Gases
Das Verhältnis der Wärmekapazitäten eines Gases bei konstantem Druck und konstantem Volumen κ=cp/cv.
Für ideale Gase kann die Poisson-Konstante aus der Anzahl der Freiheitsgrade des jeweiligen Moleküls bestimmt werden.
Mit der Taste "▼M,κ▼" übertragen Sie die Werte M und κ in die Gasdefinition unten.
Die Berechnung ermöglicht die Lösung des Zustands eines idealen Gases (pV=mrT), seiner Zustandsänderung und die Ermittlung der entsprechenden Energiewerte (Entropie, Enthalpie, Wärme, Arbeit...). Nach Auswahl (oder Definition der physikalischen Parameter) des Arbeitsgases können Sie dessen Arbeitsparameter (Masse m, Druck p, Volumen V und Temperatur T) basierend auf der Zustandsgleichung des idealen Gases bestimmen:
p * V = m * r * T
r = R / M
M = m / N
Wobei:
p ... Absoluter Druck [Pa]
V ... Volumen [m^3]
m ... Masse [kg]
T ... Temperatur [K]
R ... Universelle Gaskonstante R=8314.46261815324 [J/kmol/K]
M ... Molmasse des Gases [kg/kmol] (Luft 28.966 kg/kmol)
N ... Stoffmenge [kmol]
r ... Spezifische Gaskonstante [J/kg/K] (Luft 287.0427 J/kg/K)
A ... Beispiel eines einfachen thermodynamischen Systems, ideales Gas p⋅V=m⋅r⋅T.
B ... Reversible Prozesse können allgemeiner als polytrope Prozesse beschrieben werden, bei denen die Wärmekapazität des (geschlossenen) Systems konstant ist. Bei einem polytropen Prozess ändern sich im Allgemeinen alle Zustandsgrößen (p, V, T). Für einen polytropen Prozess in einem idealen Gas gilt die Gleichung p⋅Vn=const.. In den p-V- und T-s-Diagrammen sind die Kurven der Änderungen für verschiedene n markiert.
C ... Carnot-Kreisprozess. Beispiel einer idealen Wärmekraftmaschine, die aus zwei isothermischen und zwei adiabatischen Prozessen besteht.
D ... Kurven der grundlegenden reversiblen Zustandsänderungen:
o n=0, p=const, Isobar, (dp=0,wt=0,q=Δh,w=Δh−Δu)
o n=1, T=const, Isotherm, (dT=0,Δu=Δh=0,q=w=wt)
o n=κ, s=const, Isentrop, (ds=0,q=0,w=−Δu,wt=−Δh)
o n=∞, v=const, Isochor, (dv=0,w=0,q=Δu,wt=Δu−Δh)
Wählen Sie das Arbeitsgas aus der Liste. Falls es nicht in der Liste ist, deaktivieren Sie die Schaltfläche rechts und geben Sie die Werte M, cp und κ ein.
Mit der Temperaturänderung ändern sich cp,cv,κ des Gases. Für vordefinierte Gase können Sie eine Referenz- (Arbeits-)Temperatur definieren. Im grünen Feld wird der empfohlene Wert (Durchschnitt aus den Max/Min-Werten von T1...T6) angezeigt.
Mit der Taste "◄" übertragen Sie den empfohlenen Wert in die Eingabezelle.
Wenn Sie die Gasparameter definieren, geben Sie den Wert ein.
r = R / M
r .... spezifische Gaskonstante (Luft 287.0427 J/kg/K)
R ... Universelle Gaskonstante (8314.46261815324 J/kmol/K)
M ... Molmasse des Gases (Luft 28.996 kg/kmol)
Wenn Sie die Gasparameter definieren, geben Sie den Wert ein.
Das Verhältnis der Wärmekapazitäten eines Gases bei konstantem Druck und konstantem Volumen κ=cp/cv.
Für ideale Gase kann die Poisson-Konstante aus der Anzahl der Freiheitsgrade des jeweiligen Moleküls bestimmt werden.
Geben Sie die Stoffmenge ein. In der nächsten Zeile wird die entsprechende Masse angezeigt.
Durch Drücken der Taste "◄ N1" wird die ausgefüllte Stoffmenge der Masse m1 (Punkt 1) zugewiesen.
Durch Drücken der Taste "m1▼" wird der Massenwert in das Feld m1 (Punkt 1) verschoben.
Gleichgewichtszustand und Zustandsänderung des idealen Gases (Zustandsgleichung). Es stehen 6 Punkte (i=1−6) zur Verfügung. An jedem Punkt kann der Gleichgewichtszustand des Gases durch seine Zustandsgrößen p(i), V(i), T(i) bestimmt werden. Für die Punkte 2-6 kann bestimmt werden, wie die Zustandsänderung von Zustand (i−1) nach (i) erfolgte. Zustandsänderungen können in den Graphen "p-V" und "T-s" verfolgt werden.
Bestimmung des Gleichgewichtszustandes:
Geben Sie die Ihnen bekannten Werte nacheinander in die weißen Zellen des ausgewählten Punktes ein. In den grünen Zellen rechts werden laufend die Werte berechnet, die zum Erreichen des Gleichgewichtszustandes (p⋅V=m⋅r⋅T) verwendet werden müssen. Übertragen Sie den vorgeschlagenen Wert mit der Taste "◄" in die weiße Eingabezelle. Die Erfüllung der Gleichung wird durch den Text "▼ =OK ▼" signalisiert. Wenn die Zustandsgleichung nicht erfüllt ist, wird der Text "▼ Error ▼" angezeigt.
Zustandsänderungen:
Wenn Sie die Gasparameter am Punkt 2 (3,4...) einstellen, können Sie die Änderungen für Energiewerte (Entropie, Enthalpie, Wärme, Arbeit...) in Bezug auf den vorherigen Punkt ermitteln.
Empfohlenes Vorgehen 1: Isobare (p=konst.), isochore (V=konst.), isotherme (T=konst.) Änderung.
• Verwenden Sie die Taste "►", um den Zustand (m,p,V,T) in den nächsten Punkt zu übertragen. (Die Taste "►=" fügt einen Link zum vorherigen Punkt ein. Zum Beispiel wird p2 "=p1", V2 "=V1" usw. Die Zellenfarbe wird grau).
• Ändern Sie einen Eingangswert. Sofort werden im grünen Spalte die Werte für das Erreichen des Gleichgewichtszustandes vorgeschlagen.
• Übertragen Sie den ausgewählten Vorschlag mit der Taste "◄" in die Eingabezelle (weiß).
Empfohlenes Vorgehen 2: Polytroper Prozess - die Wärmekapazität des (geschlossenen) Systems ist dabei konstant. Bei einem polytropen Prozess ändern sich im Allgemeinen alle Zustandsgrößen (p, V, T). Für einen polytropen Prozess in einem idealen Gas gilt die Gleichung p⋅Vn=konst..
• Verwenden Sie die Taste "►", um den Zustand (m,p,V,T) in den nächsten Punkt zu übertragen.
• Ändern Sie nur einen Eingangswert (p oder V oder T).
• Geben Sie den polytropen Exponenten n ein und drücken Sie die Taste "◄ Polytr.◄". Die Eingabezellen werden mit Werten gefüllt, um das gewünschte n zu erreichen.
Mischen von Gasen - Taste "3 = Mix (1+2)"
Berechnung der Parameter eines Gases, das durch Mischen zweier Teile (1+2) mit unterschiedlichen Parametern p,V,T entsteht.
m = m1 + m2
p = m / M * R * T / V
V = V1 + V2
T = (m1 * T1 + m2 * T2) / (m1 + m2)
Reversible Prozesse können allgemeiner als polytrope Prozesse beschrieben werden, bei denen die Wärmekapazität des (geschlossenen) Systems konstant ist. Bei einem polytropen Prozess ändern sich im Allgemeinen alle Zustandsgrößen (p, V, T). Für einen polytropen Prozess in einem idealen Gas gilt die Gleichung p⋅Vn=konst.
Geben Sie den gewünschten Wert für n für den Übergang zwischen zwei Zuständen (vorheriger und aktueller) in die Eingabezelle ein. Rechts von der Eingabezelle wird der aktuelle Wert angezeigt, der aus p,V,T berechnet wurde. In der Dropdown-Liste befinden sich wichtige und häufig verwendete Werte.
- Verwenden Sie die Taste "►", um den Zustand (m,p,V,T) aus dem vorherigen Punkt zu übertragen.
- Ändern Sie nur einen Eingangswert (p oder V oder T).
- Nach Drücken der Taste "▲Polytr.▲" werden die Eingabezellen mit Werten gefüllt, um das gewünschte n zu erreichen.
Wenn n="?", sind die Werte (m,p,V,T) in den entsprechenden Punkten 1-2, 2-3,... identisch.
Für ausgewählte n-Werte gilt:
n=0, p=konst, Isobar, (dp=0,wt=0,q=Δh,w=Δh−Δu)
n=1, T=konst, Isotherm, (dT=0,Δu=Δh=0,q=w=wt)
n=κ, s=konst, Isentrop, (ds=0,q=0,w=−Δu,wt=−Δh)
n=∞, v=konst, Isochor, (dv=0,w=0,q=Δu,wt=Δu−Δh)
n=ln(p2/p1)/(ln(p2/p1)−ln(T2/T1))
n=(ln(V2/V1)−ln(T2/T1))/ln(V2/V1)
Typische polytrope Exponentenwerte:
Kolbenkompressor: n=1.2–1.3 Prozess mit teilweiser Wärmeabfuhr, typischer Wert für langsame Kompressoren mit Kühlung.
Axialkompressor: n=1.35–1.4 Hochgeschwindigkeits-Turbokompressoren mit minimaler Wärmeabfuhr, näher am adiabatischen Prozess (γ≈1.4 für Luft).
4-Takt-Benzinmotor (Kompression): n=1.3–1.35 Kompression des Kraftstoffgemisches mit teilweiser Wärmeabfuhr an die Zylinderwände.
4-Takt-Dieselmotor (Kompression): n=1.35–1.4 Höheres Verdichtungsverhältnis und Kompression reiner Luft, geringere Wärmeverluste als beim Benzinmotor.
In der Zeile werden die polytrope spezifische Wärmekapazität und der Zustand des Gases angegeben:
• "▼ =OK ▼". Der Gleichgewichtszustand ist erreicht.
• "▼ Error ▼". Falls kein Gleichgewichtszustand vorliegt.
Wenn cn="?", sind die Werte (m,p,V,T) mit dem vorherigen Punkt identisch.
Die Taste "►►" kopiert die Werte (m1,p1,V1,T1) in alle anderen Punkte.
Geben Sie die Masse des Arbeitsmediums ein. Wenn die Eingabeziffer rot ist, handelt es sich nur um einen Hinweis, dass der Wert m im vorherigen Punkt abweicht. Dies muss kein Fehler sein!
Geben Sie den absoluten Druck des Arbeitsmediums ein.
Geben Sie das Volumen des Arbeitsmediums ein.
Geben Sie die Temperatur des Arbeitsmediums ein.
Werte für die einzelnen Punkte (Zustände) in einer Tabelle.
Entropie
S1 = (cv * LN(T1) + r * LN(V1)) * m1
S2 = (cv * LN(T2) + r * LN(V2)) * m2
In der Tabelle sind die Änderungen beim Übergang vom Zustand 1 nach 2 (bzw. 2-3, 3-4...) aufgeführt. Die Zustandsänderung wird im Zustandsdiagramm p-V und T-S angezeigt. Die Anzeige in der Tabelle und im Diagramm schalten Sie mit der entsprechenden Taste ein/aus. Die Spalte "Summe" enthält die Summe der Änderungen.
Wenn n="?", sind die Werte (m,p,V,T) in den entsprechenden Punkten 1-2, 2-3,... identisch.
Für ausgewählte n-Werte gilt:
n=0, p=konst, Isobar, (dp=0,wt=0,q=Δh,w=Δh−Δu)
n=1, T=konst, Isotherm, (dT=0,Δu=Δh=0,q=w=wt)
n=κ, s=konst, Isentrop, (ds=0,q=0,w=−Δu,wt=−Δh)
n=∞, v=konst, Isochor, (dv=0,w=0,q=Δu,wt=Δu−Δh)
Entropieänderung
ΔS = S2 - S1 = (cp * Ln(T2/T1) - r * Ln(p2 / p1))*m1
ΔS = S2 - S1 = (cv * Ln(T2/T1) + r * Ln(v2 / v1))*m1
Änderung der inneren Energie
ΔU = cv*(T2 - T1) * m1
Enthalpieänderung
ΔH = cp * (T2 - T1) * m1
Polytrope Wärme.
Energieübertragung auf das System in Form von Wärme (Q>0, wenn das System Wärme aufnimmt).
Q = m * cn * (T2 - T1)
Q = -((n - kappa) / (kappa - 1)) * W
Polytrope Volumenarbeit.
Energieübertragung durch verschiedene Arbeitsformen (W>0, wenn das System Arbeit verrichtet).
W=Q-dU=m * (cn - cv) * (T2 - T1) = m * (r / (n - 1)) * (T1 - T2)
W=m * r * T1 / (n - 1) * (1 - (V1 / V2)^(n-1))
Polytrope Druckarbeit (technisch)
Wt=n * W
W ... Polytrope Volumenarbeit [J]
n .... Polytroper Exponent [~]
Es werden zwei der am häufigsten verwendeten Zustandsdiagramme angezeigt:
- Druck (p) - Volumen (V)
- Temperatur (T) - Entropie (S)
Jeder Punkt ist mit einer Ziffer gekennzeichnet. Die einzelnen Abschnitte können mit den Tasten links ein- und ausgeschaltet werden.
Komplexe Lösung der Wärmeübertragung durch eine Mehrschichtwand (max. 10 Schichten).
Die Berechnung umfasst:
- Wärmeübergang durch Strömung (Definition von Flüssigkeiten, Strömungsart, Definition der umströmten Objekte)
- Wärmeübergang durch Leitung (Definition der Wand, Dicke und Materialparameter der einzelnen Schichten)
- Wärmeübergang durch Strahlung (Wärmeabstrahlung, Bestrahlung der Wand)
- Lösung von Rohrbündeln (Wärmetauscher)
- Lösung von berippten Oberflächen
Durch die Berechnung erhalten Sie die Parameter der Wärmeübertragung U vom Medium (T1) zum Medium (T2), den Wärmewiderstand R, die Wärmestromwerte und viele weitere.
Die Berechnung ist variabel und ermöglicht auch Teilberechnungen, wie zum Beispiel:
- Ermittlung des Wärmeübergangskoeffizienten nur zwischen Wand und medium
- Ermittlung des Wärmeübergangskoeffizienten nur der Wand selbst
- Lösungen für Wände im Vakuum und Wände in direktem Kontakt mit einer Heiz- oder Kühlfläche
Die vollständige Definition einer "Wand" kann gespeichert werden, um eine Datenbank von Lösungen zu erstellen, die in weiteren Kapiteln der Berechnung verwendet werden können.
Zum Beispiel die Abkühlung/Erwärmung von Rohrleitungen und Tanks, die Berechnung von Wärmetauschern und die Lösung von Problemen, die mehrere unterschiedliche Wände enthalten.
Vorgehensweise für die vollständige Berechnung der Wärmeübertragung von Medium 1 zu Medium 2:
- Definieren Sie die Randbedingungen des Mediums
- Definieren Sie die Form und die einzelnen Schichten der Wand
- Wählen Sie die Form und die Art der Umströmung der Wandoberfläche für Medium 1 und 2.
- Definieren Sie die Parameter der Wärmeübertragung durch Strahlung für die Innen- und Außenfläche der Wand
Das Ergebnis der Berechnung ist der Gesamtwärmedurchgangskoeffizient U, der Wärmewiderstand R und die Wärmestromwerte.
Geben Sie die Temperatur des Mediums innen und außen ein.
Für ebene Wände die Temperatur links und rechts gemäß der Abbildung.
Geben Sie den Druck von Medium 1 und 2 ein.
In diesem Abschnitt wählen Sie die Wandform und definieren die Parameter der einzelnen Schichten.
Wählen Sie den Wandtyp.
Wählen Sie die Materialgruppe. Der Zeiger in der Materialtabelle (nächste Zeile) wird auf das erste Material des entsprechenden Typs eingestellt.
Die Temperaturkurven in der Wand (zylindrische und kugelförmige Fläche) werden durch eine Gerade ersetzt.
x ... Wanddicke
y ... Temperaturverlauf
Wählen Sie das Material der Schicht. Nach dem Drücken der Schaltfläche "Hinzufügen/Ersetzen" wird das ausgewählte Material entweder in die Zeile eingefügt, in der sich die aktive Zelle befindet, oder in die erste Zeile ohne Beschreibung in der nachstehenden Definitionstabelle. Wenn die Zeile bereits die Werte b, ρ, λ, Cp enthält, werden diese überschrieben. Mit der Schaltfläche "Alles löschen" entfernen Sie die Zeilen 2-10.
In der Liste sind die einzelnen Schichten der Wand aufgeführt.
Eine Schicht ist in der Wandberechnung enthalten, wenn sie eine Dicke ungleich Null hat.
Wenn die Tabelle nicht konsistent ist (z. B. eine leere Zeile), wird der Text "Check" angezeigt. Überprüfen Sie die Eingabe.
Wenn der Wandtyp zylindrisch oder kugelförmig ist, muss der Innendurchmesser der Mehrschichtwand eingegeben werden. Die Innendurchmesser der nachfolgenden Schichten werden aus der eingegebenen Schichtdicke berechnet.
Dicke der Wandschicht.
Materialdichte
Dieser Wert hat keinen Einfluss auf die Wärmeübertragungsberechnung. Er wird zur Bestimmung des Gesamtgewichts der Wand verwendet.
Wärmeleitfähigkeit
Einheitenumrechnung
1 [W/m/K] = 0.57782 [BTU/h/ft/F]
1 [BTU/h/ft/F] = 1.7306 [W/m/K]
Spezifische Wärmekapazität
Einheitenumrechnung
1 [J/kg/°K] = 0.0002388459 [BTU/lb/°F]
1 [BTU/lb/°F] = 4186.8 [J/kg/°K]
Wärmewiderstand der Wand bezogen auf die Einheit der Innenfläche
Einheitenumrechnung
1 [m²K/W] = 5.6744659 [h.ft²F/Btu]
1 [h.ft²F/Btu] = 0.17622804 [m²K/W]
Thermal resistance of the wall per unit of internal area
Die Temperatur in der ersten Zeile ist die innere (linke) Temperatur der Wand t(1).
In den weiteren Zeilen sind die Temperaturen an den Schichtgrenzen der Wand.
Gewicht der Wandschicht bezogen auf die Einheit der Innenfläche.
Bei der Wahl einer zylindrischen/kugelförmigen Fläche wird der Wert neu berechnet.
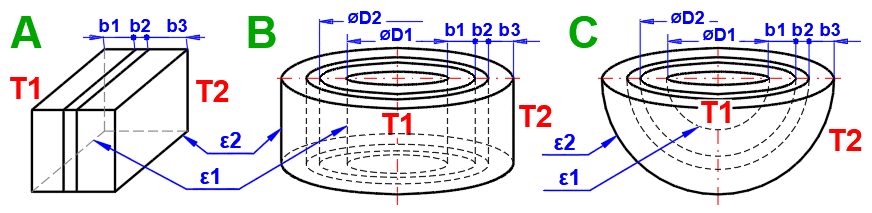
In diesem Abschnitt wird der Wärmeübergang durch Konvektion gelöst (das Medium umströmt die Oberfläche). Die Abbildung zeigt die Möglichkeiten. Für die Lösung ist es notwendig, die Parameter des Mediums, die Art der Strömung und die Parameter der umströmten Oberfläche zu definieren.
A) Erzwungene Konvektion innerhalb eines Profils (01-06)
B) Erzwungene Konvektion um ein Profil (07-13)
C) Freie Konvektion - Strömung, die durch Dichteunterschiede des erwärmten/abgekühlten Mediums ausgelöst wird (14-19)
Weiterhin können die Umströmung eines Rohrbündels und die Umströmung eines berippten Profils gelöst werden.
Die Berechnung kann auf zwei Arten verwendet werden.
A) Komplexer Wärmeübergang von Medium 1 zu Medium 2
In diesem Fall muss die Berechnungsabfolge beibehalten werden (T1=>Ts1=>Ts2=>T2). Die Kontrollkästchen unter [4.14] müssen angekreuzt sein.
B) Lösung des Wärmeübergangs zwischen Wand und Medium
Es ist möglich, die Wandtemperatur direkt einzugeben, nachdem das Kontrollkästchen bei [4.14] deaktiviert wurde. In diesem Fall wird nur der Wärmeübergang durch Konvektion für die gegebene Wand gelöst. Das gültige Ergebnis ist dann nur der Wert des Wärmeübergangskoeffizienten hc bzw. hc+hr für die ausgewählte Seite der Wand.
In der Liste befinden sich die am häufigsten gelösten Aufgaben. Durch Auswahl aus der Liste wird der entsprechende Strömungstyp 1 und 2 eingestellt und die Schalter für die Verwendung der vorgeschlagenen Werte (grünes Feld) aktiviert.
Definieren Sie hier die Parameter des Mediums innen und außen (links und rechts).
Folgende Optionen stehen zur Verfügung:
A - Vakuum. Wenn auf der Seite der Wand ein Vakuum herrscht, ist die Wärmeübertragung durch Konvektion null.
B - Direkte Verbindung. Eine Heiz-/Kühlquelle ist direkt mit der Seite der Wand verbunden, und es findet eine Wärmeübertragung mit vernachlässigbaren Verlusten statt. Zum Beispiel der Boden eines Topfes auf einem Herd.
C - Nummerierte, vordefinierte, häufig verwendete flüssige und gasförmige Stoffe. Für diese Stoffe sind die erforderlichen Parameter in Abhängigkeit von der Temperatur (Druck) definiert.
Wenn die Flüssigkeit / das Gas nicht in der Liste enthalten ist, deaktivieren Sie das Kontrollkästchen in der Zeile mit dem Dichtewert und geben Sie alle Parameter der Flüssigkeit / des Gases für die Definitionstemperatur Tdef manuell ein.
Im grünen Feld befindet sich der Wert, der das Ergebnis der vollständigen Berechnung der Wärmeübertragung von Medium 1 zu Medium 2 ist (Strahlung, Konvektion => Leitung => Konvektion, Strahlung). Dieser Wert wird durch schrittweise Iteration der Wandtemperatur ermittelt, um einen identischen Wärmestrom Q1 und Q2 zu erreichen.
Nach dem Deaktivieren des Kontrollkästchens können Sie Ihren eigenen Wert eingeben.
In diesem Fall ist das Ergebnis der Berechnung der Wärmeübergang durch Strahlung + Konvektion auf der jeweiligen Wandseite.
Kriteriengleichungen zur Berechnung des Wärmeübergangs hc von verschiedenen Autoren verwenden unterschiedliche Temperaturen zur Definition der Parameter der Flüssigkeit / des Gases.
a) Durchschnittliche Filmtemperatur an der Wand Tdef = (T + Ts)/2
b) Mittlere Temperatur Tdef = T
Bei den meisten Gleichungen wird Tdef = (T + Ts)/2 verwendet.
Wenn keine direkte Eingabe des Wertes (erste Option) gewählt ist, erfolgt bei der Wahl der Kriteriengleichung [4.23] eine automatische Umschaltung.
Dynamische Viskosität für die Wandtemperatur Ts
Dynamische Viskosität für die Definitionstemperatur Tdef
Wählen Sie den Strömungstyp. In der Liste bedeutet der erste Buchstabe:
A-Erzwungene Konvektion
B-Freie Konvektion
Die Zahl entspricht der Abbildung oben und der kleine Buchstabe nach der Zahl bestimmt die verwendete Gleichung (Quelle).
Wählen Sie den Strömungstyp für Medium 1 und Medium 2, der Ihrer Aufgabe gemäß der Abbildung oben entspricht. Die gegenseitige Kombination der Auswahl sollte sinnvoll sein. Es ist zum Beispiel nicht möglich, dass Medium 1 in einem Rohr mit kreisförmigem Querschnitt strömt und Medium 2 eine Kugel umströmt.
Eine ungeeignete Kombination wird durch einen roten Hinweis "Check" zwischen den Auswahllisten angezeigt.
**) Strömung im Ringspalt 05
Wenn diese Option (05) als innere (linke) Wand ausgewählt ist, wird der Wärmeübergang für den Außendurchmesser d1 (zwischen der strömenden Flüssigkeit und der Außenseite) gelöst.
Wenn diese Option (05) als äußere (rechte) Wand ausgewählt ist, wird der Wärmeübergang für den Innendurchmesser d2 (zwischen der strömenden Flüssigkeit und der Innenseite) gelöst.
Die zulässigen Kombinationen sind daher:
1) A-05 ... A-07 oder
2) A-01 ... A-05 (geeignet, wenn Sie Längsrippen für die Außenfläche des Rohres verwenden möchten)
Wenn der Strömungstyp A-Erzwungene Konvektion ausgewählt ist, geben Sie die Strömungsgeschwindigkeit ein.
Nach der Auswahl des Strömungstyps werden die Variablennamen und Einheiten entsprechend der Abbildung eingestellt.
Die grünen Felder enthalten die vorgeschlagenen Werte.
Rippen sind eine effektive Lösung, um die wärmeübertragende Fläche zu vergrößern und damit die Wärmeübertragung zu erhöhen.
Wenn die umströmte Oberfläche Rippen aufweist, stellen Sie den Schalter auf "Ja".
Die eigentliche Form der Rippen wird in Abschnitt 4a definiert. Sie wechseln dorthin über die Schaltfläche ">>Definition [4a]."
Basierend auf den Abmessungen der Rippen (Abschnitt 4a) wird eine neue wärmeübertragende Fläche At1, At2 bestimmt. Diese wird für den vorgeschlagenen Wert A1 und A2 [4.37] verwendet.
Durch die Rippen wird zwar die Fläche für die Wärmeübertragung vergrößert, gleichzeitig wird aber der Wirkungsgrad der Wärmeübertragung ηf1, ηf2 verringert. Mit diesem Wirkungsgrad wird der Wärmeübergangskoeffizient hc1, hc2 korrigiert.
Zur Vergrößerung der wärmeübertragenden Fläche werden häufig Rohrbündel verwendet. Wenn Sie diese Aufgabe lösen möchten, wählen Sie aus der Liste die Rohranordnung A oder B (siehe Abbildung). In den folgenden Zeilen füllen Sie die Parameter der Rohranordnung aus. Für diese Aufgabe ist es erforderlich, dass Medium 1 im Rohr (01-06) strömt und Medium 2 das Rohr umströmt (07-11).
Wenn eine falsche Kombination von Strömungstypen gewählt wird, wird der Hinweis "Check" angezeigt.
Geben Sie den Abstand zwischen den Rohren in vertikaler Richtung ST und in horizontaler Richtung SL gemäß der Abbildung ein.
Der Standardwert ist das Doppelte des Außendurchmessers des Rohrs.
Geben Sie die Anzahl der Reihen in vertikaler Richtung m und in horizontaler Richtung n gemäß der Abbildung ein.
In Abhängigkeit von der Anordnung und der Anzahl der Reihen und Spalten wird die Anzahl der Rohre im Bündel bestimmt (grüne Zelle).
Wenn sich die Anzahl der Rohre in Ihrer Aufgabe unterscheidet, können Sie einen eigenen Wert eingeben. Dies beeinflusst den Vorschlag der wärmeübertragenden Fläche.
In Zeile [4.24] geben Sie die Geschwindigkeit v2 der Strömung vor dem Eintritt in das Rohrbündel ein. Durch das Einsetzen der Rohre verkleinert sich der Strömungsquerschnitt. Dadurch erhöht sich die Strömungsgeschwindigkeit um die Rohre herum (v2max) für Medium 2.
Im grünen Feld wird ein vorgeschlagener Wert angezeigt, der auf den eingegebenen Abmessungen und der Geschwindigkeit v2 basiert. Wenn Ihre Konstruktion atypisch ist, deaktivieren Sie das Kontrollkästchen und geben Sie Ihren eigenen Wert ein.
Im grünen Feld wird ein vorgeschlagener Wert angezeigt, der auf den zuvor definierten Parametern basiert.
Für Medium 1 ist es die linke Seite (für eine Fläche) oder der innere Umfang x Rohrlänge. Für Medium 2 ist es die rechte Seite (für eine Fläche) oder der äußere Umfang x Rohrlänge.
Wenn Rippen oder Strömung durch ein Rohrbündel (Wärmetauscher) gewählt sind, wird die wärmeübertragende Fläche entsprechend geändert.
1. Rohrbündel ... A * Anzahl der Rohre
2. Rippen ... At (aus Abschnitt Rippen)
3. Bündel berippter Rohre ... Fall 1 * Fall 2
Es wird der Fall der einfachen Umströmung (ohne Rippen) überprüft, bei dem die wärmeübertragende Fläche für Medium 1 kleiner oder gleich der Fläche für Medium 2 sein sollte. Wenn dies nicht der Fall ist, werden Sie durch den Hinweis "Check" gewarnt.
Bei der Verwendung von Kriteriengleichungen zur Berechnung des Wärmeübergangskoeffizienten hc werden dimensionslose Parameter (Ähnlichkeitszahlen) verwendet, die die Lösung ähnlicher Formen unterschiedlicher Abmessungen und unterschiedlicher Umgebungsbedingungen ermöglichen. Eine detailliertere Erklärung finden Sie in der Hilfe oder in der Fachliteratur.
Die wichtigsten Ähnlichkeitszahlen sind hier aufgeführt.
Mit der Schaltfläche verschieben Sie den vorgeschlagenen (berechneten) Wert hc1, hc2 aus der grünen Zelle in die Eingabezelle. Die Iteration erfolgt 5-mal.
Die wichtigste Ähnlichkeitszahl ist die Nusselt-Zahl. Für die Berechnung des Wärmeübergangskoeffizienten hc gelten dann die folgenden Beziehungen:
Nu = hc Dh / λ ===>
hc = Nu λ / Dh
λ ... Wärmeleitfähigkeit des Wandmaterials
Dh ... Charakteristische Länge (D, Dh, a ... basierend auf der Form)
Im grünen Feld sind die berechneten Wärmeübergangskoeffizienten hc1 und hc2. Die Berechnung basiert auf den Parametern des strömenden Mediums, den Temperaturen und der Strömungsart. Wenn Sie sie verwenden möchten, drücken Sie die Schaltfläche "Iteration" hc1<<, hc2<<.
Bei einer Änderung von hc1 und hc2 ändern sich zwangsläufig die Temperaturen und damit auch die Parameter des strömenden Mediums und es erfolgt eine neue Berechnung von hc. Daher wird der Ersatz 5-mal hintereinander durchgeführt.
Kleinere Schaltflächen "hc1" und "hc2" ersetzen dann nur einen Koeffizienten.
Für jedes Medium sind zwei Werte angegeben
- Wärmestrom bezogen auf die Flächeneinheit (A1, A2)
- Gesamtwärmestrom durch die Fläche A1, A2
In diesem Teil der Berechnung werden einfache Fälle von Abstrahlung / Bestrahlung gelöst.
- Abstrahlung in den Raum (z. B. eine große Halle)
- Abstrahlung in den Raum (normale atmosphärische Umgebung)
- Bestrahlung der Fläche (z. B. Sonnenstrahlung)
Für die meisten gängigen Situationen sind diese Fälle ausreichend, wenn Sie komplexere Aufgaben im Bereich der Wärmeübertragung durch Strahlung lösen müssen, verwenden Sie den Abschnitt [7.0] und verwenden Sie das Berechnungsergebnis als positiven / negativen Strahlungsstrom, der auf die gegebene Fläche auftrifft.
Die Abbildung zeigt den Energiefluss (+) und (-) bezogen auf die Wandoberfläche 1 und 2.
Wählen Sie die Materialgruppe. Der Zeiger in der Materialtabelle (nächste Zeile) wird auf das erste Material des entsprechenden Typs eingestellt.
Die Schaltfläche "Search" versucht, in der Materialtabelle das entsprechende Material für die erste und letzte Wandschicht zu finden.
Wählen Sie das Material der Oberfläche. In der Klammer hinter dem Namen ist der typische Emissionsgrad für das ausgewählte Material angegeben. Wenn ein Wertebereich angegeben ist, wird deren Durchschnitt als vorgeschlagener Wert (grün) angeboten.
Nach dem Deaktivieren des Kontrollkästchens können Sie Ihren eigenen Wert für den Emissionsgrad der Wandoberfläche eingeben.
Bestimmen Sie, ob Wärme in den Raum abgestrahlt wird.
Wählen Sie die entsprechende Option (siehe Abbildung)
A ... Keine Wärmeübertragung durch Strahlung. Es handelt sich um eine geschlossene Fläche (z. B. die Innenwand einer Rohrleitung).
B ... Allgemeine Abstrahlung in den Raum (innen und außen). Zur Berechnung der Wärmeübertragung durch Strahlung wird die Temperatur des Mediums T1 bzw. T2 in Bezug auf die Wandtemperatur Ts1 bzw. Ts2 verwendet.
Wenn Sie die Bedingungen nicht genau kennen, wählen Sie diese Option.
C, D, E ... Zur Bestimmung der Strahlung zwischen der Wand und dem Himmel wird die äquivalente Temperatur des Himmels für einen schwarzen Körper Tsky [°K] festgelegt. Diese Temperatur berücksichtigt die Ungleichmäßigkeit der Temperatur der Atmosphäre und die Abstrahlung in bestimmten Wellenlängen.
Berechnung des Wärmestroms qr' = ε σ (Tsky^4 - Ts^4)
Für die Beziehung zwischen der Temperatur des Himmels und der lokalen Lufttemperatur werden Näherungsbeziehungen verwendet:
C ... Tsky = Ta - 6°C
D ... Tsky = Ta - 12°C
E ... Tsky = 0.0552 Ta^1.5 (Gültigkeitsbereich -30...+50°C)
wobei Ta ... Temperatur der Umgebungsluft [°K] (zum Beispiel: Ta = T2[°C] + 273.15)
Im grünen Feld wird der vorgeschlagene Wert der Abstrahlfläche angezeigt. Wenn keine Rippen oder Rohrbündel verwendet werden, ist die Fläche Ar1, Ar2 identisch mit der wärmeübertragenden Fläche A1 bzw. A2. [4.37]
Wenn Rippen oder Strömung durch ein Rohrbündel gewählt sind, wird die Abstrahlfläche entsprechend geändert.
1. Rohrbündel ... A * Anzahl der Randrohre / 2
2. Rippen ... A + Fläche der Randrippen
3. Bündel berippter Rohre ... Fall 1 * Fall 2
Für jedes Medium sind zwei Werte angegeben
- Wärmestrom bezogen auf die Flächeneinheit (A1, A2)
- Gesamtwärmestrom durch die Fläche A1, A2
Wenn Sie eine andere Wärmeübertragung durch Strahlung als die Abstrahlung in den Raum lösen müssen. Z.B.: Sonnenstrahlung, Daten aus Abschnitt [7.0], eigene Berechnung ....
Geben Sie die Intensität der auf die Fläche einfallenden Strahlung ein. Mit dem Schalter rechts stellen Sie ein:
- * 1: Die Berechnung verwendet den direkt eingegebenen Wert und berücksichtigt nicht den Emissionsgrad der Wand ε. Es wird angenommen, dass der Emissionsgrad bereits in der Größe der Strahlung enthalten ist. Zum Beispiel das Ergebnis der Berechnung aus Ab
- * ε: Die Berechnung multipliziert den eingegebenen Wert mit dem oben gewählten Emissionsgrad ε der Wand. Es wird angenommen, dass die Strahlungsintensität bekannt ist. Zum Beispiel Sonnenstrahlung.
Sonnenstrahlung
Ihr Maximalwert auf der Erdoberfläche liegt bei etwa 1100 [W/m²] (350 [Btu/h/ft²]). Für genaue Werte verwenden Sie den Abschnitt [8.0].
Geben Sie die Größe der bestrahlten Fläche Ai ein / Wählen Sie sie aus.
Nach der Auswahl des ersten Eintrags aus der Liste können Sie die Größe der bestrahlten Fläche Ai direkt eingeben.
Die weiteren Einträge 1-5 (siehe Abbildung) ermöglichen die Berechnung der bestrahlten Fläche Ai aus der wärmeübertragenden Fläche A1, A2 in Abhängigkeit von ihrer Form.
Für jede Seite der Wand sind zwei Werte angegeben
- Durchschnittlicher Wärmestrom bezogen auf die Flächeneinheit A1, A2 (da nur ein Teil der wärmeübertragenden Fläche bestrahlt werden kann, wird der Eingabewert "ir" mit dem Verhältnis Ai/A multipliziert).
- Gesamtwärmestrom durch die Fläche
Summe aller Komponenten.
Wärmeübergangskoeffizient für die entsprechende Seite der Wand. Er umfasst Konvektion, Abstrahlung und Bestrahlung.
Wärmestrom für die entsprechende Seite der Wand. Er umfasst Konvektion, Abstrahlung und Bestrahlung.
Die Berechnung berücksichtigt keine mögliche Temperaturänderung des strömenden Mediums.
qcri' = qc' + qr' + qi' ... spezifisch bezogen auf die Einheit der inneren / äußeren Fläche
Qcri = Qc + Qr + Qi ... gesamt
Für jedes Medium sind zwei Werte angegeben
- Wärmestrom bezogen auf die Flächeneinheit
- Gesamtwärmestrom durch die Fläche A1, A2
Für verschiedene weitere Berechnungen ist es notwendig, den Gesamtwärmedurchgangskoeffizienten U bzw. den Wärmewiderstand R=1/U zu kennen. In den Berechnungen werden verwendet:
1) Werte bezogen auf die innere (1) oder äußere (2) Fläche. Sie gelten auch für Zylinder und Kugeln.
2) Werte bezogen auf die Einheitslänge des definierten Zylinders [4.5, 4.8].
3) Werte bezogen auf die definierte Kugel [4.5, 4.8].
In der Literatur und in Katalogen wird häufig der Parameter "Wärmewiderstand der Wand" angegeben. Es handelt sich dabei nur um den Wärmewiderstand der Mehrschichtwand, die in der obigen Tabelle definiert ist.
Zur schnellen Orientierung wird auch die Berechnung für die Erwärmung / Abkühlung des Arbeitsmediums angegeben, wenn die gelöste Aufgabe dies zulässt (vollständige Berechnung, lange Rohrleitungen, lange umströmte Flächen usw.).
Mit dem Schalter zwischen den Überschriften wählen Sie, ob die Medien gleichläufig oder gegenläufig strömen.
Unten geben Sie die Parameter des strömenden Mediums für die innere (linke) Seite und für die äußere (rechte) Seite der Wand für die Temperaturen T1 und T2 ein.
Bei der Berechnung des vorgeschlagenen Durchflussquerschnitts (grüne Zelle) können folgende Fälle auftreten:
1) Die Flüssigkeit strömt durch einen genau definierten Querschnitt (01-06). Der Wert im grünen Feld ist genau. Z.B. Rohr mit kreisförmigem Querschnitt Af = PI * (D/2)^2
2) Die Flüssigkeit umströmt eine Rohrleitung (07-11). Es wird ein Wert vorgeschlagen, der dem senkrechten Schnitt der Rohrleitung (Außenabmessung) entspricht. Z.B. kreisförmiges Rohr Af = D * L
3) Die Flüssigkeit strömt durch ein Rohrbündel. Af = m * ST * L
4) Freie Konvektion (13-19). Der Durchflussquerschnitt entspricht der umströmten Fläche.
Nach dem Deaktivieren des Kontrollkästchens können Sie Ihren eigenen Wert eingeben.
Aus der eingegebenen Strömungsgeschwindigkeit v1 (v2) [4.24], der Durchflussfläche Af und der Dichte Rho wird der Durchfluss berechnet.
In der Liste rechts können Sie die Einheiten auswählen, die angezeigt werden.
Aus der eingegebenen wärmeübertragenden Fläche A [4.37], dem Durchflussquerschnitt Af, der Dichte Rho, der spezifischen Wärmekapazität Cp', dem Durchfluss m' und dem berechneten Wärmeübergangskoeffizienten U wird die Temperatur am Ausgang Tout1 und Tout2 berechnet.
Der Wärmestrom wird aus der Differenz der Medientemperaturen am Ein- und Ausgang und aus den Eigenschaften des Arbeitsmediums berechnet.
Der Wärmestrom unterscheidet sich daher von den Werten Qcri [4.62], bei denen die Temperaturänderung des Mediums nicht berücksichtigt wird.
Für jedes Medium sind zwei Werte angegeben
- Durchschnittlicher Wärmestrom bezogen auf die Flächeneinheit
- Gesamtwärmestrom durch die Fläche A1, A2
Die Lösung der Wärmeübertragung durch die Wand erfordert die Eingabe und Auswahl von Dutzenden von Parametern. Daher ist es möglich, die Lösung zu benennen und mit einem Kommentar zu versehen und sie in einer Liste für die zukünftige Verwendung oder zum Laden von Parametern in anderen Abschnitten dieser Berechnung zu speichern.
Der aktuelle Status aller Parameter - die Lösung - speichern Sie mit der Schaltfläche "Lösung speichern".
Die Lösungen werden auf dem Arbeitsblatt "Wände" gespeichert. Eine Zeile enthält eine gespeicherte Lösung.
Wenn Sie die Schaltfläche "Lösung speichern" drücken, wird die Liste durchsucht und wenn ein Eintrag mit demselben Namen existiert, wird er mit dem aktuellen Status überschrieben. Wenn der Name nicht in der Liste der Lösungen existiert, wird die letzte ausgefüllte Zeile auf dem Arbeitsblatt "Wände" gefunden und die aktuelle Lösung in die nächste Zeile geschrieben.
Das Arbeitsblatt "Wände" ist frei zugänglich und kann mit den Excel-Funktionen normal bearbeitet werden (z. B. Löschen unnötiger Lösungen - Zeilen).
Ermittlung eines einzelnen Wertes aus einer gespeicherten Lösung.
Wenn Sie einen bestimmten Wert ermitteln und in Ihrer eigenen Formel verwenden möchten, steht die Funktion GetWallProp zur Verfügung, die dies ermöglicht.
Syntax:
GetWallProp(ID;value_name)
ID ... Zeilennummer auf dem Arbeitsblatt "Wände", die die gespeicherte Lösung enthält
value_name ... Name des Wertes, den Sie ermitteln möchten.
Geben Sie den Namen der Lösung der Wärmeübertragung durch die Wand ein.
Unter diesem Namen wird die Lösung in der Liste der gespeicherten Lösungen gespeichert.
Automatisch generierter Text, der zur Beschreibung hinzugefügt wird und grundlegende Informationen enthält, in denen sich befinden:
T1(),T2() ... Temperaturen, (Medium)
|mm| ... Wanddicke
U1 ... Wärmeübergangskoeffizient
q1,q2 ... Gesamtspezifischer Wärmestrom
Geben Sie eine Beschreibung ein. Dies ermöglicht Ihnen eine bessere Orientierung beim späteren Durchsuchen der bereits gespeicherten Lösungen.
Nach der Auswahl der Lösung aus der Auswahlliste unten drücken Sie die Schaltfläche "Lösung laden".
Mit den Schaltflächen rechts bewegen Sie sich in der Liste der gespeicherten Lösungen.
Das Speicherdatum der Lösung hat das Format "yyyymmdd - hh:mm:ss".
Die Auswahlliste enthält Lösungen der Wärmeübertragung durch die Wand, die auf dem Arbeitsblatt "Wände" gespeichert sind.
Grundlegende Informationen zur ausgewählten Lösung der Wärmeübertragung durch die Wand.
Beschreibung der ausgewählten Lösung der Wärmeübertragung durch die Wand.
Dieser Abschnitt ist direkt an den vorherigen Abschnitt angebunden und behandelt die Berippung der umströmten Fläche. Sie wird zur Vergrößerung der Wärmeübertragungsfläche und damit zur Steigerung der Wärmeübertragung verwendet. Für die Nutzung muss die Berippung im vorherigen Abschnitt [4.29] aktiviert sein.
Basierend auf der im vorherigen Abschnitt [4.23] gewählten Strömungsart wird der entsprechende Rippentyp 1-4 gemäß der Abbildung zugewiesen.
Aus dem vorherigen Abschnitt [4.0] werden die Werte λ, hc, T und Ts für die Berechnung der Berippung verwendet. Für die Wärmeleitfähigkeit des Materials λ wird der Wert der ersten und letzten Schicht der Verbundwand verwendet.
Abhängig von der Wahl der Strömungsart [4.23] und den eingegebenen Abmessungen wird die Breite des Rippenfeldes „a“ für den jeweiligen Rippentyp berechnet:
1) a = Flächenlänge
2) a = Rohrlänge
3) a = Innenumfang des Rohrs
4) a = Außenumfang des Rohrs
Nach dem Deaktivieren der Schaltfläche können Sie einen eigenen Wert für die Feldbreite eingeben.
Wählen Sie die Rippenform gemäß der Abbildung.
Basierend auf den Abmessungen der berippten Fläche und der Strömungsart sind die Rippenabmessungen voreingestellt (grüne Zellen). Nach dem Deaktivieren der Schaltfläche können Sie Ihre eigenen Abmessungen eingeben.
In der grünen Zelle wird die maximale Anzahl an Rippen vorgeschlagen, die im Verhältnis zur Feldbreite und den Rippenabmessungen verwendet werden kann. Nach dem Deaktivieren der Schaltfläche können Sie einen eigenen Wert eingeben. Zum Beispiel, wenn nur ein Teil der Fläche / des Rohrs berippt ist.
- Af ... Fläche einer einzelnen Rippe (nur die Rippe).
- At ... Gesamte Wärmeübertragungsfläche (Rippenfläche x Anzahl der Rippen + verbleibende Fläche des Grundprofils).
Der Wert der gesamten berippten Wärmeübertragungsfläche At wird als empfohlener Wert in Zeile [4.37] verwendet.
Der Parameter x dient dazu, den Rippenwirkungsgrad in den entsprechenden Diagrammen zu finden (er führt die Berechnung durch).
Der Gesamtwirkungsgrad umfasst das Verhältnis der Rippenfläche zur gesamten berippten Fläche und wird bei der Berechnung des Wärmestroms qc', Qc [4.43] verwendet.
Dieser Abschnitt befasst sich mit der Temperaturänderung eines strömenden Mediums in der Rohrleitung und der Abkühlzeit für eine vorgegebene Temperaturabsenkung in Rohrleitungen, Behältern und Speichern.
Wählen Sie das Medium, das in der Rohrleitung strömt.
Falls das Medium nicht in der Liste enthalten ist, geben Sie den Cp-Wert in Zeile [5.3] ein.
Geben Sie die Definitionstemperatur ein. Aus der Temperatur wird der Cp-Wert für das ausgewählte Medium in Zeile [5.3] berechnet.
Der voreingestellte Wert (grünes Feld) ist die Temperatur T1 aus Abschnitt [4.0].
Nach dem Deaktivieren der Schaltfläche können Sie Ihren eigenen Cp-Wert eingeben.
Die Berechnung ermöglicht die Bestimmung der Temperatur des strömenden Mediums in der Rohrleitung in einem vorgegebenen Abstand vom Eingang.
Es wird davon ausgegangen, dass die Umgebungstemperatur konstant ist.
Die Phasenumwandlungstemperatur des Mediums wird nicht überprüft.
In den grünen Feldern befinden sich die Entwurfswerte aus Abschnitt [4.0].
Nach dem Deaktivieren der Schaltfläche können Sie Ihre eigenen Werte eingeben.
Es ist erforderlich, den Wärmedurchgangskoeffizienten bezogen auf die Einheitslänge der Rohrleitung einzugeben.
Der Pw-Wert gibt die Verlustleistung (-) oder die zugeführte Leistung (+) an.
Die Berechnung ermöglicht die Bestimmung der Abkühlzeit eines Mediums in einem Speicher (Behälter, Rohrleitung) von der Temperatur T1s auf die Temperatur T1e.
Es wird davon ausgegangen, dass die Umgebungstemperatur konstant ist.
Die Phasenumwandlungstemperatur des Mediums wird nicht überprüft.
In den grünen Feldern befinden sich die Entwurfswerte aus Abschnitt [4.0].
Nach dem Deaktivieren der Schaltfläche können Sie Ihre eigenen Werte eingeben.
Geben Sie die Endtemperatur ein, die Sie erreichen möchten. Das Ergebnis der Berechnung ist die Zeit, die erforderlich ist, um die Temperatur T1e zu erreichen.
Geben Sie die Masse des Mediums im Speicher (Behälter, Rohrleitung) ein.
Geben Sie den Wärmedurchgangskoeffizienten bezogen auf die Einheit der Innenfläche des Speichers ein.
Der Wert E gibt den Energieverlust (-) oder den Energiegewinn (+) an.
Dieser Abschnitt behandelt die grundlegenden Typen von Wärmeübertragern (Gleichstrom, Gegenstrom, Gleichstrom+Gegenstrom, zusammengesetzter Gleichstrom+Gegenstrom, Kreuzstrom).
Wählen Sie den entsprechenden Wärmeübertrager-Typ, den Sie berechnen möchten. Richten Sie sich bei der Auswahl nach den Abbildungen A-G. Die Berechnung behandelt grundlegende Aufgaben. Es ist jedoch auch möglich, sie zur Lösung komplexerer Wärmeübertrager-Typen zu verwenden, wenn Sie deren Korrekturfaktor kennen [6.17].
Die Berechnung des Wärmeübertragers hängt vom korrekt bestimmten Gesamtwärmedurchgangskoeffizienten U ab. Diesen bestimmen Sie genau in Abschnitt [4.0]. Sie können entweder die aktuellen Werte aus Abschnitt [4.0] laden oder eine gespeicherte Wandlösung aus der Liste auswählen und deren Werte übernehmen.
Wenn Sie den Gesamtwärmedurchgangskoeffizienten kennen, können Sie ihn direkt in Zeile [6.21] eingeben. Die Hilfestellung enthält auch charakteristische Werte für häufige Konfigurationen.
Nach dem Drücken der Schaltfläche rechts werden geladen:
- Gesamtwärmedurchgangskoeffizient
- Auswahl des Arbeitsmediums
- Temperaturen T1, T2
- Massenstrom
Wählen Sie die im Wärmeübertrager verwendeten Arbeitsmedien. Wenn ein Medium nicht in der Liste enthalten ist, geben Sie den Wert für Cp1 und Cp2 in Zeile [6.7] ein.
Geben Sie die Definitionstemperatur ein. Anhand der Temperatur wird der Cp-Wert für das gewählte Medium in Zeile [6.7] berechnet. Der voreingestellte Wert (grünes Feld) ist der Durchschnitt der Temperaturen T1in und T1out (bzw. T2in und T2out für T2def).
Durch Deaktivieren der Schaltfläche können Sie einen eigenen Cp-Wert eingeben.
Berechnung des Wärmestroms Q für die eingegebenen Parameter des Massenstroms und der Temperaturen der Arbeitsmedien.
Die folgenden Zeilen geben die Parameter der Arbeitsmedien 1 und 2 an (Massenstrom, Eintrittstemperatur, Austrittstemperatur). Im grünen Feld befindet sich der Entwurfswert, der für das Erreichen eines Wärmestromgleichgewichts (Gültigkeit von Q1 = - Q2) erforderlich ist. Neben dem grünen Feld befindet sich die Schaltfläche "◄", die den Entwurfswert in den Eingangswert verschiebt.
Bei jeder Änderung eines beliebigen Eingangswertes werden die entsprechenden Werte zur Erreichung des Wärmestromgleichgewichts (Q1 = - Q2) in den grünen Zellen neu berechnet.
Zum Beispiel eine unsinnige Lösung der Art:
- Arbeitsmedium 1 mit einer Temperatur von T1
Der Wärmestrom zwischen Medium 1 und 2. Der Wärmestrom muss betragsmäßig übereinstimmen (+/-). Basierend auf dem Wärmestrom kann anschließend die Größe der Wärmeübertragungsfläche bestimmt werden.
Nach der Definition des Massenstroms, der Temperaturen und somit des Wärmestroms wird die mittlere logarithmische Temperaturdifferenz ΔT' ermittelt. Diese ist für die Berechnung der erforderlichen Wärmeübertragungsfläche notwendig.
Die Koeffizienten R und P sind für die Bestimmung von ɛ [6.17] notwendig.
R … Das Wärmekapazitätsverhältnis R
R = (T1Kin - T1Kout) / (T2Kout - T2Kin)
P ... Die Temperatur-Effizienz P
P = (T2Kout - T2Kin) / (T1Kin - T2Kin)
Entsprechende ɛ-Diagramme für viele Wärmeübertrager-Typen sind in der angegebenen Literatur verfügbar.
Für komplexere Wärmeübertrager-Typen wird zur Bestimmung der mittleren logarithmischen Temperaturdifferenz ein Korrekturfaktor ɛ verwendet. Für Wärmeübertrager vom Typ C-G wird dieser durch Annäherung aus Tabellen bestimmt (diese befinden sich auf dem Blatt "Tabellen").
Für Wärmeübertrager, die in diesem Programm nicht definiert sind, kann der Koeffizient ɛ aus den R-P-ɛ-Diagrammen bestimmt werden, die in der Fachliteratur zu finden sind (z.B. *Heat Exchanger Design Handbook* und andere). Diagramme werden meistens für viele Wärmeübertrager-Typen angegeben.
Die Größe des Koeffizienten liegt im Bereich von 0.5-1.0.
Der Wärmeübertrager kann als Platten- oder Rohrbündelwärmeübertrager berechnet werden. Meistens entscheidet die Konstruktion des Wärmeübertragers darüber, welche Methode vorteilhafter ist. Wählen Sie den Typ aus der Liste.
- Plattenwärmeübertrager
Der Gesamtwärmedurchgangskoeffizient U ist pro Flächeneinheit definiert.
Für den erforderlichen Wärmestrom wird die Wärmeübertragungsfläche berechnet.
- Rohrbündelwärmeübertrager
Der Gesamtwärmedurchgangskoeffizient U ist pro Längeneinheit des Rohres definiert.
Für den erforderlichen Wärmestrom wird die Rohrlänge berechnet.
Wenn Sie die Wanddefinition aus Abschnitt [4.0] oder aus der Liste laden, befindet sich der entsprechende Wert im grünen Feld. Wenn Sie einen eigenen Wert eingeben möchten, deaktivieren Sie die Schaltfläche.
Richtwerte für Upl für verschiedene Flüssigkeitskombinationen in Wärmeübertragern.
Je nach der Wahl des Typs [6.19] wird die erforderliche Fläche oder die Rohrlänge berechnet.
Durch die Berechnung ermitteln Sie die Austrittstemperaturen T1Out und T2Out in Abhängigkeit von der Größe der Wärmeübertragungsfläche oder der Rohrlänge.
Geben Sie die Größe der Wärmeübertragungsfläche bzw. die Rohrlänge ein.
Für die eingegebenen Parameter:
- m1', m2' ... [6.9]
- T1in, T2in ... [6.10]
- Upl oder Ucyl ... [6.21]
- A oder L ... [6.24]
finden Sie die Austrittstemperaturen T1Out und T2Out.
Durch Drücken der Schaltfläche "▲T1out, ▲T2out" werden die berechneten Werte in die Zeile [6.11] übernommen.
Eine einfache Umrechnung der Fläche in die Rohrlänge und umgekehrt. Je nachdem, welcher Wärmeübertrager-Typ gewählt wurde [6.19], wird die Fläche [6.22] in die Rohrlänge oder die Rohrlänge [6.22] in die Fläche umgerechnet.
- Wählen Sie das Rohrprofil aus der Liste (A-E)
- Geben Sie die Fläche oder die Rohrlänge ein (voreingestellter Wert aus [6.22])
- Geben Sie die Profilabmessungen gemäß der Abbildung ein (voreingestellte Werte sind gemäß der geladenen Wand [6.3, 6.4])
Im Betrieb kann es zu Belägen oder Oxidation auf der Oberfläche kommen. Dies erhöht den Widerstand und verringert die Leistung des Wärmeübertragers. Die Widerstandserhöhung wird durch den Verschmutzungsfaktor Rf = 1/Ud - 1/Uc [m²K/W], [h·ft²F/Btu] ausgedrückt.
Der Koeffizient wird experimentell ermittelt oder es kann eine Tabelle mit empfohlenen Werten [6.35] für verschiedene Medien verwendet werden.
Geben Sie den flächenbezogenen Gesamtwärmedurchgangskoeffizienten für die saubere Oberfläche ein.
Geben Sie den Verschmutzungsfaktor Rf ein. Wenn Sie den Wert nicht kennen (z.B. aus einer Messung), können Sie sich an den Werten aus der Tabelle orientieren. Wenn beide Flächen des Wärmeübertragers verschmutzt sind (innen und außen), geben Sie die Summe der Rf-Werte an.
Der Gesamtwärmedurchgangskoeffizient für die verschmutzte Oberfläche und die prozentuale Differenz zwischen Uc und Ud. Verringern Sie den Upl- (Ucyl-) Wert [6.21] um die entsprechende prozentuale Differenz.
Mit der Schaltfläche "▲U" verringern Sie den Upl- (Ucyl-) Wert [6.21] direkt.
Die durchschnittliche Temperatur (Tin+Tout)/2 wird gestrichelt angezeigt.
Blau ... Medium 1
Grün ... Medium 2
Tauschen
Durch Klicken auf die Schaltfläche "<---->" tauschen Sie Medium 1 und Medium 2 aus.
In diesem Abschnitt werden grundlegende Aufgaben der Wärmeübertragung durch Strahlung behandelt.
A…Strahlung in den Raum (Fläche, Zylinder, Kugel, allgemeine Form)
Für die Strahlung in den freien Raum in der Erdatmosphäre wird oft die Beziehung Tsky = Lufttemperatur - 6°C oder Tsky = Lufttemperatur - 12°C verwendet (Schätzung, die den Einfluss der atmosphärischen Strahlung berücksichtigt). Für den Weltraum kann Tsky = -270°C verwendet werden.
B…Strahlung zwischen zwei parallelen Oberflächen (Fläche, Zylinder, Kugel)
C…Strahlung zwischen zwei parallelen Oberflächen mit einer Abschirmfolie x (Fläche, Zylinder, Kugel)
D…Strahlung zwischen zwei parallelen Oberflächen mit zwei Abschirmfolien x,y (Fläche, Zylinder, Kugel)
Annahmen und Vereinfachungen:
1) Das Medium zwischen den Oberflächen muss diatherman sein. Der Medientyp (Vakuum, Gastyp...) wird nicht behandelt.
2) Für die Berechnung wird eine Folie mit "null" Dicke und "unendlicher" Wärmeleitfähigkeit angenommen.
3) Im Falle einer ebenen Fläche muss der Abstand der Flächen um Größenordnungen kleiner sein als die Abmessungen der Flächen.
4) Im Falle einer zylindrischen Fläche wird angenommen, dass die Zylinderlänge L um Größenordnungen größer ist als der Durchmesser D.
5) Es ist möglich, einen unterschiedlichen Emissionsgrad der Abschirmfolie für jede Seite der Folie zu wählen.
6) Im Falle nicht konzentrischer Flächen (4) sind nur die Werte für den gesamten Wärmestrom Q12 gültig.
Je nach gewählter Aufgabe sind die Eingabesektionen - die grauen Felder - deaktiviert.
Wählen Sie die Materialgruppe. Der Zeiger in der Materialtabelle (nächste Zeile) wird auf das erste Material des entsprechenden Typs eingestellt.
Nach dem Deaktivieren der Schaltfläche können Sie einen eigenen Wert im Bereich [0…1] eingeben.
Geben Sie die Wandtemperatur T1, T2 ein.
Wenn Strahlung in den Raum behandelt wird, geben Sie die Raumtemperatur Tsky ein.
Wählen Sie aus der Liste den Flächentyp aus.
1. Ebene Fläche: Die eingegebene Fläche (1) wird auf die Flächen 2, X, Y projiziert.
2. Zylinder-Fläche: Die Länge des Zylinders von (1) wird auf 2, X, Y projiziert. Die Durchmesser des Zylinders können beliebig in 1, 2, X, Y gewählt werden, unter der Bedingung, dass D1.
3. Kugel-Fläche: Die Durchmesser können beliebig in 1, 2, X, Y gewählt werden, unter der Bedingung, dass D1.
4. Allgemeine Fläche: Sie ist für die Berechnung des Wärmestroms zwischen der Fläche 1 bestimmt, die vollständig in der Fläche 2 eingeschlossen ist. Die Größe der Fläche kann beliebig in 1, 2, X, Y gewählt werden, unter der Bedingung, dass A1. Die Form der gegenseitigen Flächen wird nicht behandelt, und dadurch kann auch die Temperatur der Abschirmfolie x,y ungenau sein.
Bei der allgemeinen Fläche wird angenommen, dass die Flächen in keiner Weise ineinander eingeschlossen sind.
Basierend auf der Auswahl und den Daten der vorherigen Zeile wird der berechnete Wert der Fläche A angeboten. Nach dem Deaktivieren der Schaltfläche können Sie einen eigenen Wert eingeben.
Bedingung: A1<=Ax<=Ay<=A2. Ein roter Text weist auf die Nichterfüllung der Bedingung hin.
Die Parameter der Abschirmfolien sind ähnlich wie bei der Wand, wobei eine Folie mit "null" Dicke und "unendlicher" Wärmeleitfähigkeit angenommen wird und es ist notwendig, den Emissionsgrad beider Seiten direkt einzugeben.
Geben Sie den Emissionsgrad der Abschirmfolie für die linke und rechte Seite ein. Die Werte aus der obigen Liste können als Richtlinie dienen.
Ist abhängig von der Auswahl [7.07].
Für Zylinder und Kugel kann der Durchmesser gewählt werden. Die anderen Werte sind durch Oberfläche 1 definiert.
Nach dem Deaktivieren der Schaltfläche geben Sie einen eigenen Wert ein.
Bedingung: A1<=Ax<=Ay<=A2. Ein roter Text weist auf die Nichterfüllung der Bedingung hin.
Es sind zwei Werte angegeben.
1) Spezifischer Wärmestrom pro Flächeneinheit. Wenn die Fläche A1<>A2 (Zylinder, Kugel, allgemeine Fläche) ist, sind die Werte für jede Fläche unterschiedlich.
2) Gesamtwärmestrom für die eingegebene Fläche.
In diesem Abschnitt wird die grundlegende thermische Belastung durch Sonneneinstrahlung behandelt (Dauer, Uhrzeit, Ort, Flächenausrichtung ...).
Eine Vielzahl von Maschinenbau- (und Bau-) Konstruktionen ist der Sonneneinstrahlung ausgesetzt. Die Berechnung dient zur Bestimmung des solaren Wärmestroms auf eine Fläche unter den vorgegebenen Bedingungen (Flächenausrichtung, Datum, Stunde, Höhe, Verschmutzung) und zur Bestimmung der gesamten täglichen Leistung.
Mit der Taste "▼▼" stellen Sie das aktuelle Datum und die aktuelle Uhrzeit ein.
Geben Sie den Monat und den Tag ein, für die Sie den Wert des Sonnenflusses ermitteln möchten.
Mit den Tasten -/+ können Sie die Eingabewerte ändern und die Änderungen in den Diagrammen verfolgen.
Die Zahl zwischen den Tasten - und + gibt die Schrittweite an.
Ein ungültiger Tag wird rot hervorgehoben.
Geben Sie die Stunde und den Breitengrad ein, für die Sie den Wert des Sonnenflusses ermitteln möchten.
Mit den Tasten -/+ können Sie die Eingabewerte ändern und die Änderungen in den Diagrammen verfolgen.
Die Zahl zwischen den Tasten - und + gibt die Schrittweite an.
Breitengrade von Städten.
Geben Sie die Neigung der Fläche zur horizontalen Ebene ein (0=horizontal, 90=senkrecht).
Geben Sie den Azimut der Flächennormalen ein (0=S, 90=W, -90=E, 180=N).
Beispiel: SW-Ausrichtung=45.
Mit den Tasten -/+ können Sie die Eingabewerte ändern und die Änderungen in den Diagrammen verfolgen.
Die Zahl zwischen den Tasten - und + gibt die Schrittweite an.
Die Zeiten für Sonnenaufgang und Sonnenuntergang (für die Sonnenmitte) sind als Richtwerte zu verstehen. Sie berücksichtigen nicht den Längengrad, Sommer-/Winterzeit usw.
Die Dauer des Sonnenscheins für die eingegebenen Parameter.
Wenn die Kombination aus Datum und Breitengrad zu Folgendem führt:
Polartag … Sonnenaufgang/Sonnenuntergang = 0/24, Sonnenscheindauer = 24
Polarnacht … Sonnenaufgang/Sonnenuntergang = 12/12, Sonnenscheindauer = 0
Der Sonnenhöhenwinkel φ ist der Winkel zwischen der Sonne und dem (idealen) Horizont für die angegebenen Parameter MM,TT,HH.
Die Sonnendeklination δ ist der Winkel der Sonne zur Äquatorebene für das angegebene Datum MM,TT.
(φ=0) ... Sonnenaufgang und Sonnenuntergang: Der Moment, in dem der geometrische Mittelpunkt der Sonne den Horizont kreuzt.
(φ'-6) ... Die bürgerliche Dämmerung beginnt bzw. endet in dem Moment, in dem sich die Mitte der Sonnenscheibe 6° unter dem Horizont befindet. Während der bürgerlichen Dämmerung können im Freien ohne künstliche Beleuchtung normale Aktivitäten wie das Lesen einer Zeitung oder das Spielen von Ballspielen durchgeführt werden.
(φ'-6...-12) ... Nautische Dämmerung: Während der nautischen Dämmerung befindet sich die Mitte der Sonnenscheibe zwischen 6° und 12° unter dem Horizont. Die ersten Sterne sind sichtbar und gleichzeitig ist der Horizont deutlich erkennbar.
(φ'-18) ... Astronomische Dämmerung: Die astronomische Dämmerung bringt die ersten und letzten Sonnenstrahlen des Tages. Der Himmel ist sehr dunkel, Sterne sind deutlich sichtbar. Wenn die Sonne weiter als 18° unter den Horizont sinkt, beginnt die astronomische Nacht. Wenn die Sonne um die Sommersonnenwende nicht mehr als 18° unter den Horizont sinkt, verschmilzt die astronomische Abenddämmerung mit der Morgendämmerung und die astronomische Nacht tritt nicht ein.
Der solare Strahlungsfluss außerhalb der Atmosphäre ändert sich im Laufe des Jahres um +/-3.3% (Entfernung Erde-Sonne). Der Wert bei mittlerer Entfernung Erde-Sonne beträgt 1367 W/m².
Weitere Einstellungen präzisieren den Strahlungsfluss in Bezug auf die Atmosphäre, die Verschmutzung usw.
Die Höhe über dem Meeresspiegel definiert die Dicke und Dichte der Luftschicht, die die Wärmestromdichte beeinflusst.
Durch die Auswahl aus der Auswahlliste wird der Wert in die Eingabezelle übertragen.
Bezieht die Auswirkungen der Luftverschmutzung für verschiedene Gebiete und Jahreszeiten mit ein.
Z=1 ... Passage durch völlig saubere Luft
Z=2 ... Bergregionen
Z=3 ... Landschaft
Z=4 ... Stadt
Z=>5 ... Industriegebiet
Für Winterperiode - 20%
Für Sommerperiode + 10%
Durch die Auswahl aus der Auswahlliste wird der Wert in die Eingabezelle übertragen.
γs ... Der Azimut der Sonne ist der Winkel zwischen Süden (S) und der Position der Sonne für die eingegebenen Werte.
Θ ... Der Einfallswinkel der Sonneneinstrahlung ist der Winkel zwischen der Verbindungslinie der Sonnenmitte und der Flächennormalen "n" für die eingegebenen Werte.
QbT ... Reeller Wert der Strahlung, die auf die definierte geneigte Fläche (Neigung und Ausrichtung) trifft.
Qbn ... Strahlung, die auf eine senkrechte Fläche (zur Sonnenposition) trifft, nachdem sie die Atmosphäre durchquert hat, für die eingegebenen Daten (Datum, Ort, Verschmutzung...).
QdT ... Diffuse Sonneneinstrahlung auf die gegebene Fläche.
Qdt = ((1 + cos(beta)) / 2) * Qd
Qd ... Es wird eine vereinfachte Schätzung verwendet, bei der davon ausgegangen wird, dass etwa ein Drittel der Sonnenstrahlung, die in der Atmosphäre "verloren geht", auf die horizontale Fläche trifft.
Qd = 0.33 * (Qon - Qbn)
Albedo - Das Verhältnis zwischen der reflektierten und der einfallenden Dichte des solaren Strahlungsflusses. Für die Berechnungen kann Rhog = 0.2 verwendet werden.
Werte:
0.10 bis 0.15 ... Übliche Vegetation
0.90 ... Schnee
0.35 - 0.45 ... Erdoberfläche: Land
0.05 - 0.10 ... Erdoberfläche: Meer
0.30 (Durchschnitt) ... Albedo der Erde (Planet)
QrT ... Reflektierte Sonneneinstrahlung auf eine gegebene Fläche.
Qrt = Rhog * ((1 - cos(beta)) / 2) * (Qb + Qg)
Geben Sie die Größe der bestrahlten Fläche ein.
Die gesamte Sonneneinstrahlung auf eine allgemein ausgerichtete Fläche für die angegebene Zeit und den angegebenen Ort. Die Summe aller Komponenten (direkt, diffus, reflektiert).
QT ... Gesamtenergie auf der angegebenen Fläche
QT' ... Energie pro Flächeneinheit
Dieser Wert gibt an, wie viel der Sonnenstrahlung in nutzbare Energie umgewandelt wird. Im Allgemeinen können die folgenden Werte gewählt werden. Genaue Werte finden Sie beim Hersteller oder Lieferanten.
Direkte Umwandlung in Elektrizität:
Photovoltaik-Module - Der Wirkungsgrad moderner Module (Jahr 2025) liegt im Bereich von 18-24% (bei 25C). Er ist temperaturabhängig, im Sommer bis zu -20%, im Winter bis zu +10%.
Warmwasserbereitung, Heizung:
Der Wirkungsgrad hängt von der Temperatur des erwärmten Mediums, der Konstruktion usw. ab. Die folgenden Richtwerte können verwendet werden. Die Temperatur des Arbeitsmediums ist in Klammern angegeben.
Flachkollektoren - 95% (0C), 70% (40C), 40% (80C), 20% (100C)
Vakuumröhrenkollektoren: 70% (0C), 55% (40C), 40% (80C), 30% (120C), 20% (140C)
Die Sonneneinstrahlung multipliziert mit dem Wirkungsgrad.
(spezifisch pro Flächeneinheit, gesamt für die Fläche)
Die Leistung der Fläche für den angegebenen Tag unter der Annahme null Bewölkung (spezifisch pro Flächeneinheit, gesamt für die Fläche).
In Abhängigkeit vom eingegebenen Breitengrad wird die Zeit für Sonnenaufgang und Sonnenuntergang für die Tage 1-365 angezeigt.
Deklination ... Der Winkel der Sonne zur Äquatorebene (δ) für den Tag (1-365).
Anzeige des Werteverlaufs für die Tage 1-365:
- Solarkonstante (Qon) [W/m²].
- Sonnenhöhe über dem Horizont (φ) für die angegebene Stunde.
- Strahlungsleistung (Qbn) [W/m²] auf eine senkrecht zur Sonne stehende Fläche für die angegebene Stunde.
Anzeige des Werteverlaufs für jede Stunde (0-24):
- Sonnenhöhe über dem Horizont
- Gesamtwert der Sonneneinstrahlung (QT=QbT+QdT+QrT)
- Einzelne Komponenten QbT, QdT, QrT
Die Werte sind in [W/m²].
Excel enthält das Add-in "Solver", ein integriertes Werkzeug zur Lösung von linearer und nichtlinearer Programmierung. Wenn komplexere Wärmeübertragungsaufgaben gelöst werden müssen, können hier die Daten für dieses Add-in übersichtlich vorbereitet werden. Auf diese Weise kann ein Modell entworfen und beispielsweise Aufgaben gelöst werden, bei denen gleichzeitig Wärmeübertragung in mehreren verschiedenen Wänden stattfindet. Dieser Abschnitt befindet sich auf einem separaten, nicht gesperrten Blatt mit dem Namen "Solver" (das zweite Blatt).
Vorgehensweise:
1. Bereiten Sie eine Tabelle der gelösten Wärmeübertragungen für die einzelnen Wände vor [9.6].
2. Definieren Sie das mathematische Modell mithilfe von Excel-Beziehungen. [9.5, 9.6, 9.7].
3. Verwenden Sie das Add-in "Solver", um das Modell zu lösen.
In Abschnitt [4.0] wird die Wärmeübertragung für eine Wand behandelt. Sie können aktuelle Werte oder Werte aus der Tabelle der gespeicherten Lösungen in die Tabelle unten übertragen.
Wählen Sie eine Wandlösung aus der Liste aus. Nach dem Drücken der Schaltfläche "Hinzufügen/Ersetzen" wird die ausgewählte Lösung entweder in die Zeile, in der sich die aktive Zelle befindet, oder in die erste Zeile ohne Beschreibung in der Definitionstabelle unten eingefügt. Wenn die Zeile bereits Werte enthält, werden diese überschrieben. Mit der Schaltfläche "Alles löschen" entfernen Sie alle Zeilen.
Wählen Sie in der Auswahlliste aus, welcher Wert in die entsprechende Spalte übertragen werden soll. Wenn Sie das erste Element "Nicht ausfüllen" auswählen, bleibt der ursprüngliche Wert in der Spalte erhalten.
Die Notation ist die gleiche wie in Abschnitt [4.0].
Zwei Spalten, die Sie für verschiedene Zwischenberechnungen verwenden können.
Bereiten Sie in der Tabelle die Werte für alle Wände vor, die Sie im mathematischen Modell für den "Solver" verwenden.
Die Verwendung des Add-ins "Solver" erfordert die Definition eines mathematischen Modells, das die zu lösende Aufgabe beschreibt.
Zur Vereinfachung und Übersichtlichkeit sind drei Bereiche vorbereitet (Eingabewerte, Ausgabewerte und Bedingungen). Hier können Sie das entsprechende mathematische Modell mithilfe von Excel-Formeln übersichtlich definieren.
Selbstverständlich können Sie das Layout und die Definition des mathematischen Modells ganz nach Ihren eigenen Anforderungen vorbereiten. Es ist nicht notwendig, sich an die vorgeschlagene Anordnung zu halten.
Die Ausführung des Add-ins "Solver" finden Sie im Excel-Menü (Menüband) "Daten".
Ein einfaches, anschauliches Beispiel für eine Aufgabe, die Modelldefinition und die Ausführung des "Solvers" in drei Schritten. Das Beispiel löst die Größe der Wärmequelle QH, um die Temperatur T2 in einem Raum mit vier verschiedenen Wänden und einer Umgebungstemperatur T2 zu erreichen.
Die folgenden Beispiele werden nachstehend gelöst:
Beispiel 01 - Periodensystem der Elemente - Gasgemischparameter (m, r, κ) - Luft
Beispiel 02 - Periodensystem der Elemente - Gasparameter (m, r, κ) -
Schwefelwasserstoff
Beispiel 03 - Ideales Gas - Füllen einer Druckflasche
Beispiel 04 - Ideales Gas - Volumenänderung durch Energiezufuhr (isobare
Zustandsänderung)
Beispiel 05 - Ideales Gas - Mischen von Gasen mit unterschiedlichen Parametern
(m, p, V, T)
Beispiel 06 - Ideales Gas - Polytrope Kompression (Verdichter)
Beispiel 07 - Ideales Gas - Kreislauf eines Kolbenverdichters
Beispiel 08 - Komplexer Wärmeübergang durch ein zylindrisches Rohr (Strahlung,
Konvektion, Wärmeleitung)
Beispiel 09 - Speichern und Laden von Wärmeübertragungslösungen durch Wände,
Ermittlung von Werten
Beispiel 10 - Partielle Wärmeübertragungslösung (Strahlung oder Konvektion oder
Wärmeleitung)
Beispiel 11 - Wärmeübertragung durch eine Wand mit Vakuum auf einer Seite
(Thermosflasche)
Beispiel 12 - Wärmeübertragung durch eine Rippenwand, die von einer Seite
kontaktiert beheizt wird (TEG-Stromgenerator)
Beispiel 13 - Wärmeübertragung - Bündel runder Rohre (10 x 8)
Beispiel 14 - Wärmeübertragung - Bündel runder Rippenrohre (7 x 6)
Beispiel 15 - Temperaturänderung und Abkühlzeit einer Flüssigkeit in einem
Behälter (Thermosflasche)
Beispiel 16 - Wärmetauscher - Gegenstrom (Wasser / Öl)
Beispiel 17 - Wärmetauscher - Einfach - Kreuzstrom mit beiden ungemischten
Flüssigkeiten
Beispiel 18 - Wärmeübertragung durch Strahlung zwischen zwei parallelen Flächen
Beispiel 19 - Wärmeübertragung durch Strahlung zwischen zwei parallelen Flächen
mit einer Abschirmfolie
Beispiel 20 - Sonnenstrahlung - Werte für eine orientierte Fläche, geografische
Lage, Zeit und Umgebung
Beispiel 21 - Wärmebilanz Gebäude: Solver, Wärmeübertragung im Objekt, Heizung,
Raumtemperaturen
Berechnung der Gasgemischparameter - Luft (Molare Masse ... M, Spezifische Gaskonstante ... r, Adiabatenexponent ... κ).
Luft: eine Mischung aus N2+O2+Ar+CO2
Massenanteil: (N2...75.518, O2...23.1354, Ar...1.288, CO2...0.059)
Geben Sie das Gasgemisch ein und verwenden Sie die Schaltfläche, um die Tabelle zu füllen.
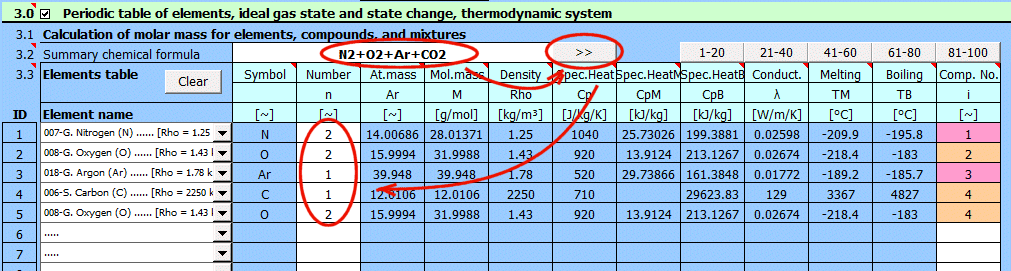
Geben Sie den Massenanteil jeder Komponente ein, um die erforderlichen Werte des Gasgemisches zu bestimmen.

Verwenden Sie die Schaltfläche "▼M,κ▼", um die Werte in die Berechnung der idealen Gasparameter zu übertragen.
Berechnung der Gasparameter - Schwefelwasserstoff (Molare Masse ... M, Spezifische Gaskonstante ... r, Adiabatenexponent ... κ).
Formel: H2S
Geben Sie die Formel ein.

Der Massenanteil beträgt 100%.
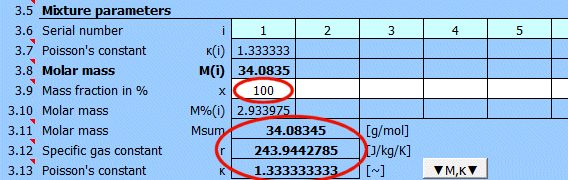
Verwenden Sie die Schaltfläche "▼M,κ▼", um die Werte in die Berechnung der idealen Gasparameter zu übertragen.
Wählen Sie Luft als Arbeitsmedium und stellen Sie die Temperatur ein.

Geben Sie die Eigenschaften für einen atmosphärischen Druck von 101 kPa ein.
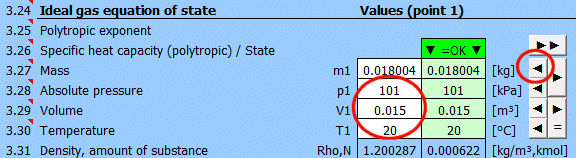
Geben Sie den neuen Druck 20 MPa = 20000 kPa ein und drücken Sie die Taste.
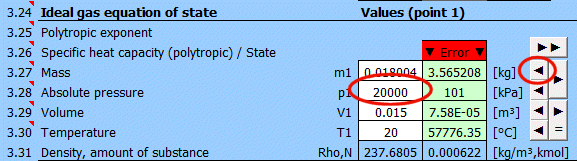
Das Ergebnis ist die neue Masse des Flascheninhalts.
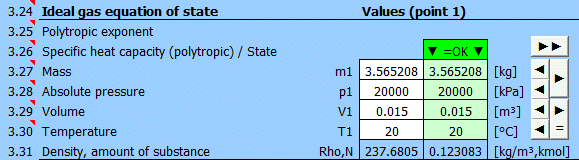
Die Masse erhöht sich um 3.565 - 0.0182 = 3.5468 kg.
Luft befindet sich in einem Zylinder unter einem Kolben. Dem Zylinder werden 300 kJ Wärme zugeführt. Bestimmen Sie die Änderung von T und V, p1=p2.
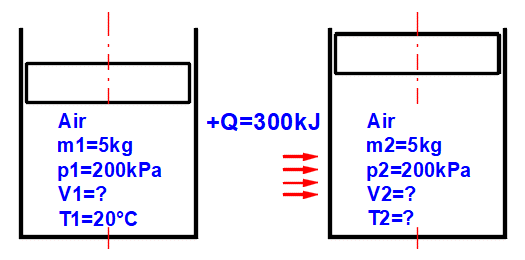
Wählen Sie Luft als Arbeitsmedium und stellen Sie die Temperatur ein.

1. Geben Sie die Werte für m1, p1, T1 ein.
2. Drücken Sie die Taste "◄", um V1 zu füllen.
3. Verwenden Sie die Taste "►►", um die Werte auf andere Punkte zu kopieren.
4. Ändern Sie die Temperatur T2 schrittweise, bis der Q-Wert 300 kJ beträgt.
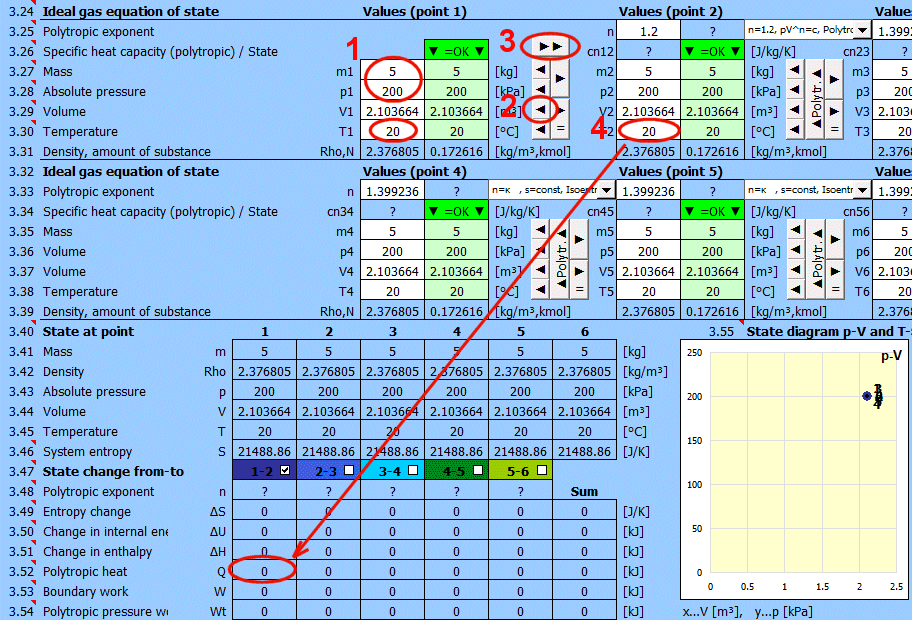
Drücken Sie die Taste "◄", um V2 zu füllen.
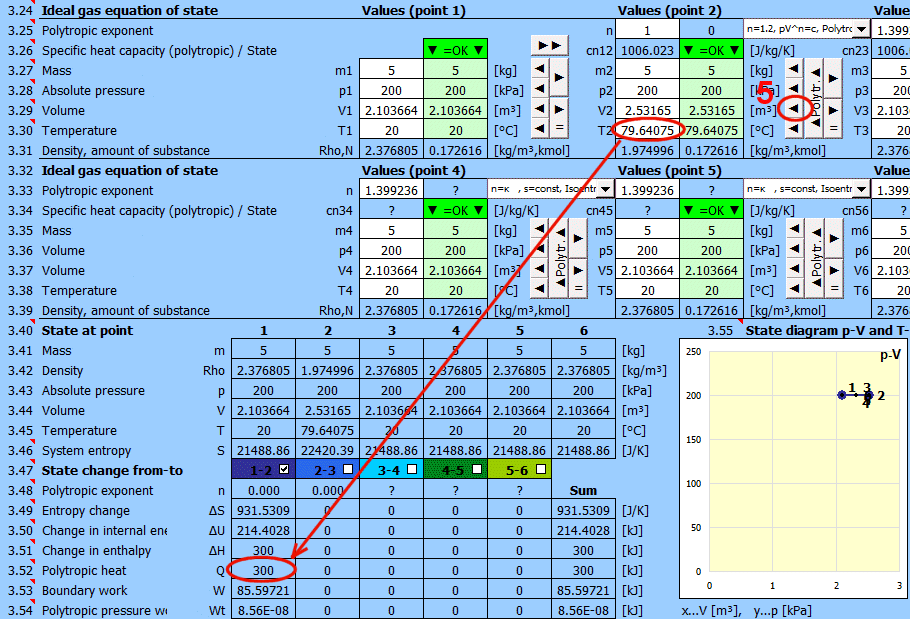
Zwei miteinander verbundene Behälter enthalten Luft mit unterschiedlichen Parametern. Nach dem Öffnen des Verbindungsventils mischen sich die Gase und kühlen dann auf eine Endtemperatur von 25 °C ab.
Bestimmen Sie den Enddruck, die Endtemperatur, die Energieänderung...
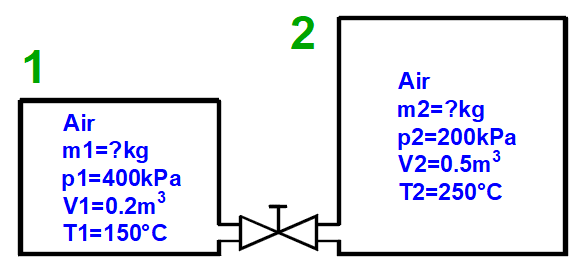
Wählen Sie Luft als Arbeitsmedium und schätzen Sie die Temperatur auf 100 °C.

1. Stellen Sie die Parameter für Behälter 1 ein.
2. Geben Sie die entsprechende Gasmasse m1 ein.
3. Stellen Sie die Parameter für Behälter 2 ein.
4. Geben Sie die entsprechende Gasmasse m2 ein.
5. Drücken Sie die Taste, um die Parameter des resultierenden Gemisches zu
berechnen.
Punkt 3 zeigt die berechneten Gasparameter, die nach dem Mischen von 1+2 auftreten.
6. Übertragen Sie die resultierenden Parameter auf Punkt 4.
7. Geben Sie die Endtemperatur des gesamten Systems T4 ein.
8. Geben Sie den entsprechenden Gasdruck p4 ein.
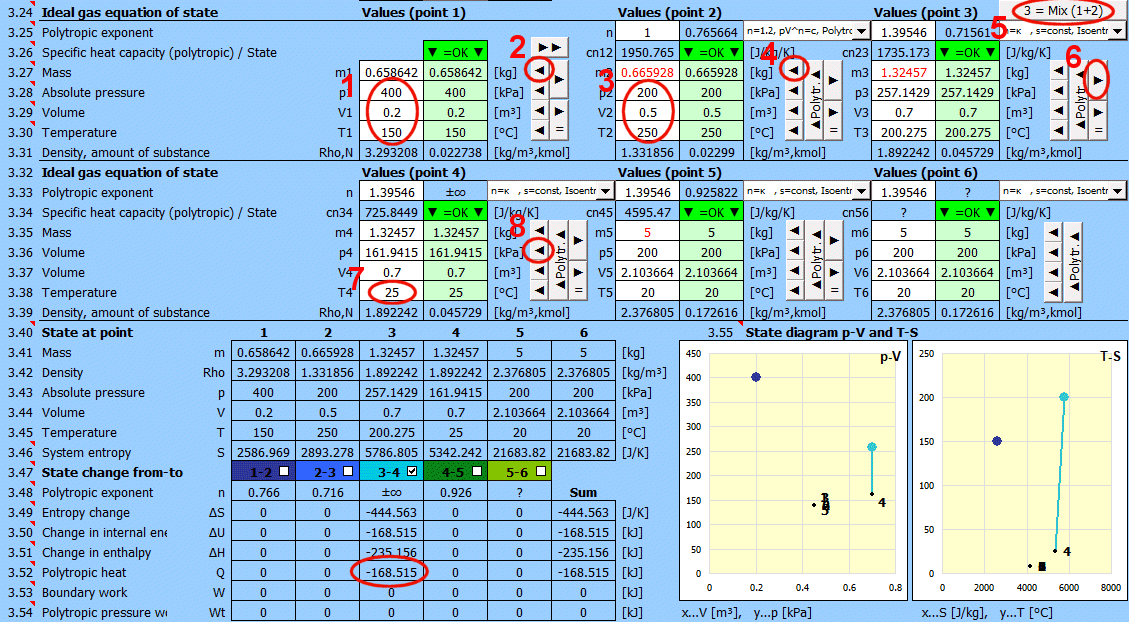
Die Energieänderung (abgeführte Wärme Q) ist die Änderung zwischen 3-4. Zum Abkühlen des Gemisches (von Punkt 3) müssen 168 kJ Wärme abgeführt werden.
Bei einem polytropen Vorgang ändern sich im Allgemeinen alle Zustandsgrößen (p,
V, T). Für den polytropen Vorgang in einem idealen Gas gilt die Gleichung p *
V^n = const.
Für einen Kolbenverdichter: n=1,2–1,3 (Prozess mit teilweiser Wärmeabfuhr,
typischer Wert für langsame Verdichter mit Kühlung).
Anfangsparameter der Luft: m1=?, p1=150 kPa, V1=260 m}^3, T1=27 °C.
Die Luft wird von einem Kolbenverdichter mit einem polytropen Exponenten n=1,2
verdichtet.
Endwerte: m2=m1, p2=?, V2=80 m^3, T2=?
Wählen Sie Luft als Arbeitsmedium und stellen Sie die Temperatur ein.

1. Stellen Sie die Luftparameter am Anfangspunkt 1 ein.
2. Füllen Sie die entsprechende Gasmasse m1 mit der Taste "◄" aus.
3. Kopieren Sie die Werte mit der Taste "►►" in die anderen Punkte.
4. Füllen Sie das Endvolumen nach der Kompression V2 aus.
5. Geben Sie den gewünschten polytropen Exponenten n=1,2 ein.

6. Drücken Sie die Taste "Polytr.".
Dies berechnet und ergänzt die Parameter p2 und T2, die dem angegebenen polytropen Exponenten n=1,2 entsprechen.
7. Ergebnisse:
Enddruck p2 = 617 kPa
Endtemperatur T2 = 106,8 °C
Druckarbeit Wt = 62,2 MJ (17,27 kWh)
An die Umgebung abgeführte Wärme Q = 25,8 MJ
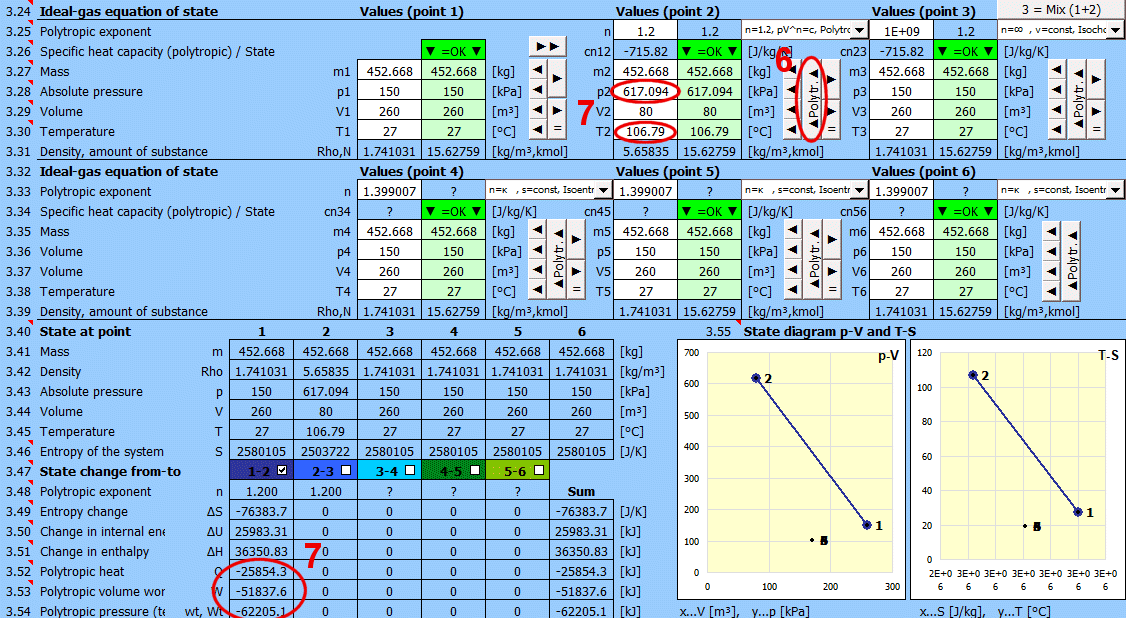
Berechnung eines Kolbenverdichters (Hubraum 1 Liter).
Arbeitsmedium: Luft
Arbeitsvolumen: V1 = 0,001 m^3
Polytroper Exponent: n=1,3 (Kolbenverdichter mit teilweiser Wärmeabfuhr,
typischer Wert für langsame Verdichter mit Kühlung).
Saugdruck: p1=100 kPa
Auslassdruck: p2=500 kPa
Temperatur der angesaugten Luft: T1=25 °C
Schädlicher Raum X: 5% => V3 = 0,00005 m^3 (Aus konstruktiven Gründen ist keine
vollständige Gasverdrängung möglich. Das Restgas expandiert und verringert das
Volumen des angesaugten Gases).
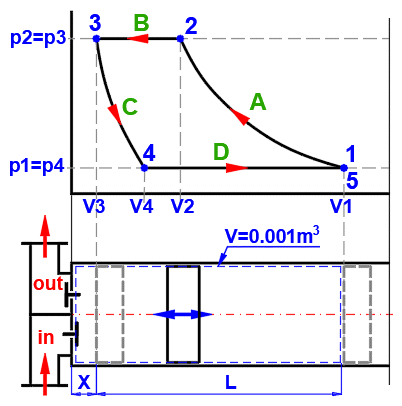
Wählen Sie Luft als Arbeitsmedium und stellen Sie die Temperatur ein.
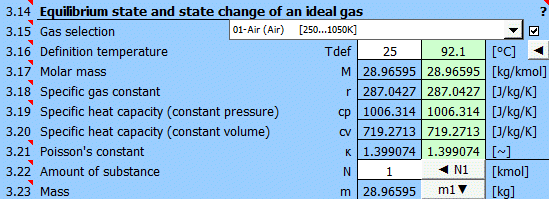
1. Stellen Sie die Parameter am Punkt 1 ein (p1=100 kPa, V1=0,001 m^3, T1=25
°C), füllen Sie m1 mit der Taste "◄" aus.
2. Kopieren Sie die Werte mit der Taste "►►" in die anderen Punkte.
3. Geben Sie den Auslassdruck p2=500 kPa und den polytropen Exponenten n=1,3
ein.
4. Drücken Sie die Taste "Polytr.".
Dies berechnet und ergänzt die Parameter V2 und T2, die dem angegebenen
polytropen Exponenten n=1,3 entsprechen.
5. Kopieren Sie die Ergebnisse mit der Taste "►" in Punkt 3.
6. Geben Sie das Endvolumen des Ausstoßes V3 = 0,00005 m^3 ein und füllen Sie m3
mit der Taste "◄" aus.
7. Kopieren Sie die Ergebnisse mit der Taste "►" in Punkt 4.
8. Geben Sie den Saugdruck p4=100 kPa und den polytropen Exponenten n=1,3 ein.
9. Drücken Sie die Taste "Polytr.".
Dies berechnet und ergänzt die Parameter V4 und T4, die dem angegebenen
polytropen Exponenten n=1,3 entsprechen.
Das Gas expandiert in den Zustand p4=p1 (Saugdruck).
10. Kopieren Sie die Ergebnisse mit der Taste "►" in Punkt 5.
11. Geben Sie das Endvolumen des Ansaugens V5 = 0,001 m^3 ein und füllen Sie m5
mit der Taste "◄" aus.
12. Aktivieren Sie die Anzeige des Zustands im p-V-Diagramm. (Die
Übergangskurven werden als Geraden dargestellt).
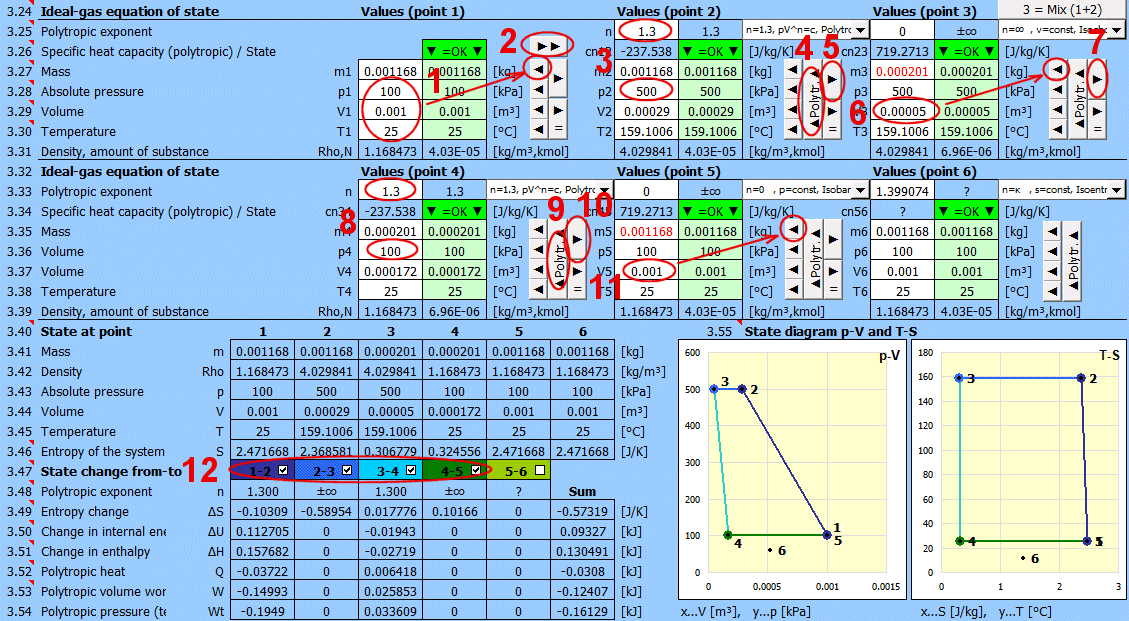
In einem Stahlrohr mit kreisförmigem Querschnitt von d=102 mm
Innendurchmesser, 3 mm Wandstärke und L=200 m Länge fließt Wasser mit einer
Temperatur von T1=90 °C und einer Geschwindigkeit von v1=0,1 m/s. Das Rohr ist
mit einer 20 mm dicken Mineralwollisolierung, einer 1 mm dicken äußeren
PVC-Schicht versehen und weiß gestrichen. Das Rohr befindet sich im Freien und
ist einer Luftströmung mit einer Temperatur von T2=10 °C und einer
Geschwindigkeit von v2=3 m/s ausgesetzt. Die Rohrleitung wird von der Sonne mit
einer Intensität von 1000 W/m^2 bestrahlt.
Lösen Sie den Wärmeverlust und die Wassertemperatur am Rohrende.
1. Geben Sie die Temperaturen T1 und T2 ein.
2. Wählen Sie den Wandtyp.
3. Definieren Sie schrittweise die Wandschichten (Abmessungen und physikalische
Eigenschaften). Materialien können aus der Liste [4.7] ausgewählt und mit der
Taste "Add" hinzugefügt werden.
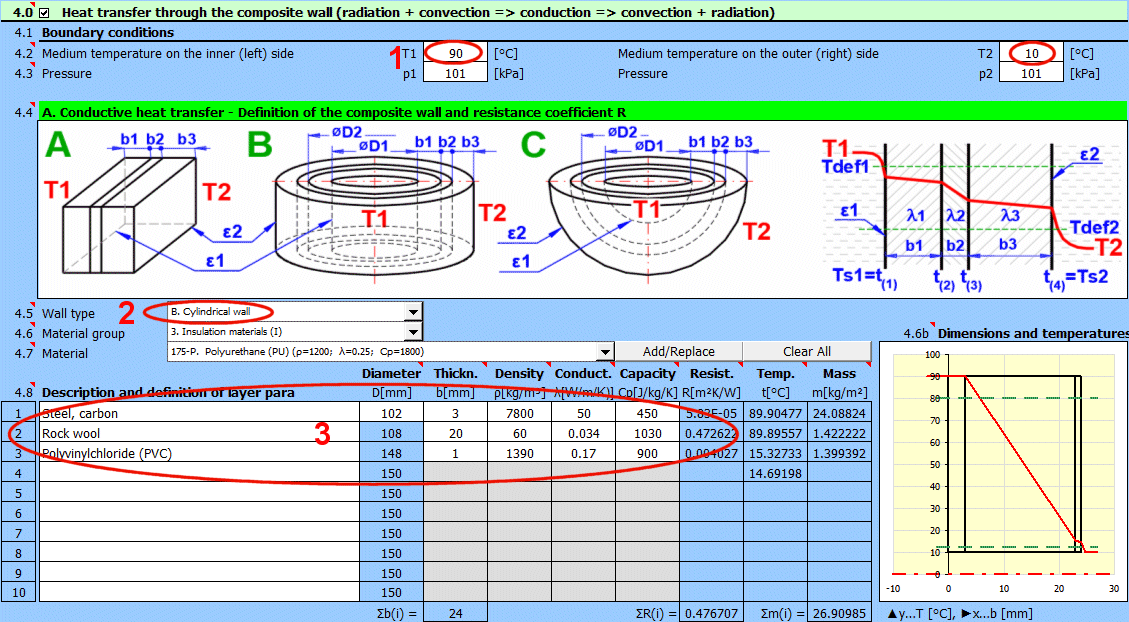
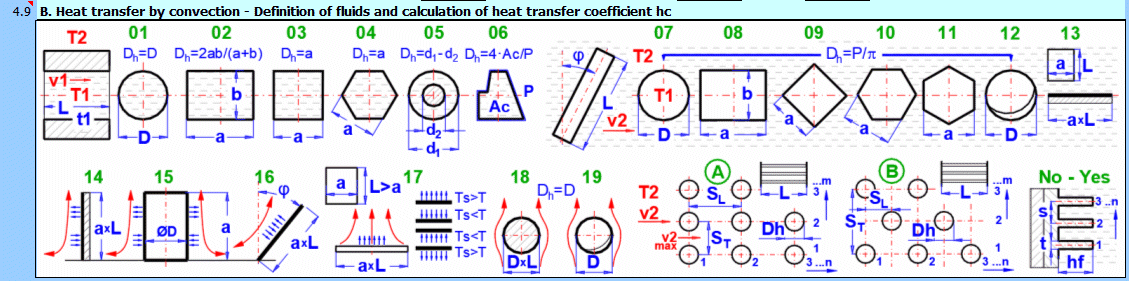
4. Wählen Sie die Arbeitsmedien 1 und 2.
5. Wählen Sie den Strömungstyp = Form der umströmten Fläche.
6. Geben Sie die Strömungsgeschwindigkeit und die Abmessungen ein.
7. Drücken Sie die Taste für die schrittweise Iteration der Ergebnisse.
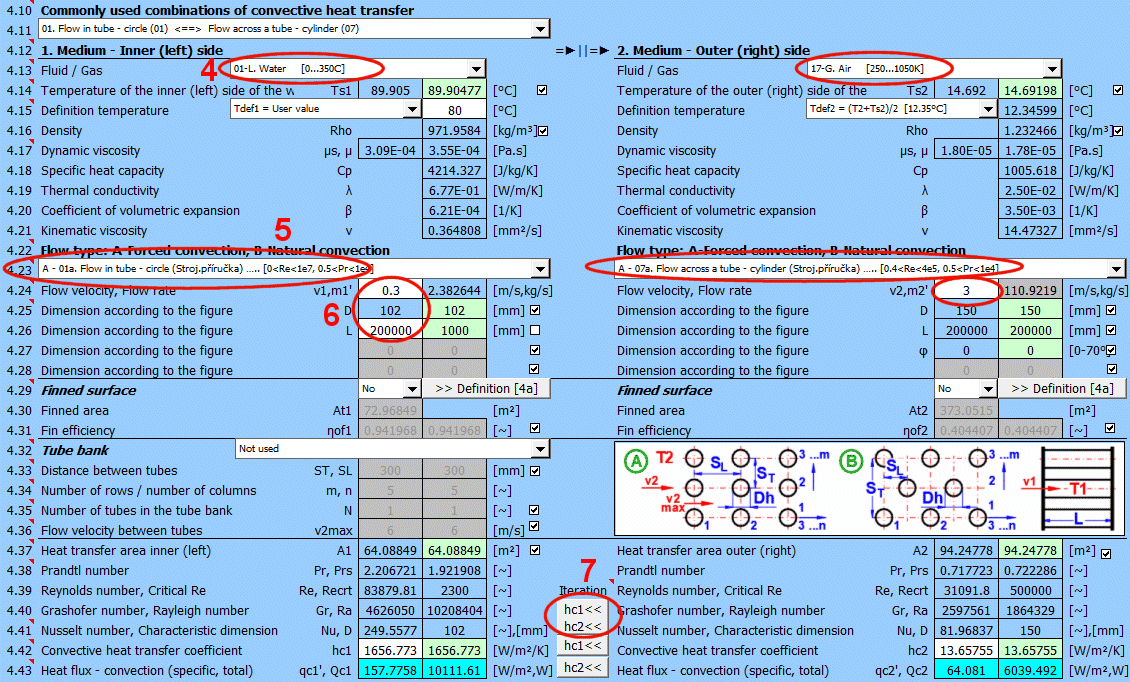
Wir lösen ein geschlossenes Profil, daher ist es nicht notwendig, sich mit der Strahlung auf der Innenseite des Rohres (Medium 1) zu befassen.
8. Wählen Sie den Oberflächentyp oder geben Sie die Emissivität ε2
direkt bei [4.45] ein.
9. Wählen Sie die Wärmeabstrahlung in den Raum.
10. Geben Sie die Strahlungsstärke ein und wählen Sie aus der Auswahlliste den
Eintrag "*
ε" - die Emissivität aus [4.45] wird verwendet.
11. Wählen Sie die Größe der bestrahlten Fläche Ai2 in Bezug auf die Fläche A2.
(Die Sonne bestrahlt nicht die gesamte Rohroberfläche).
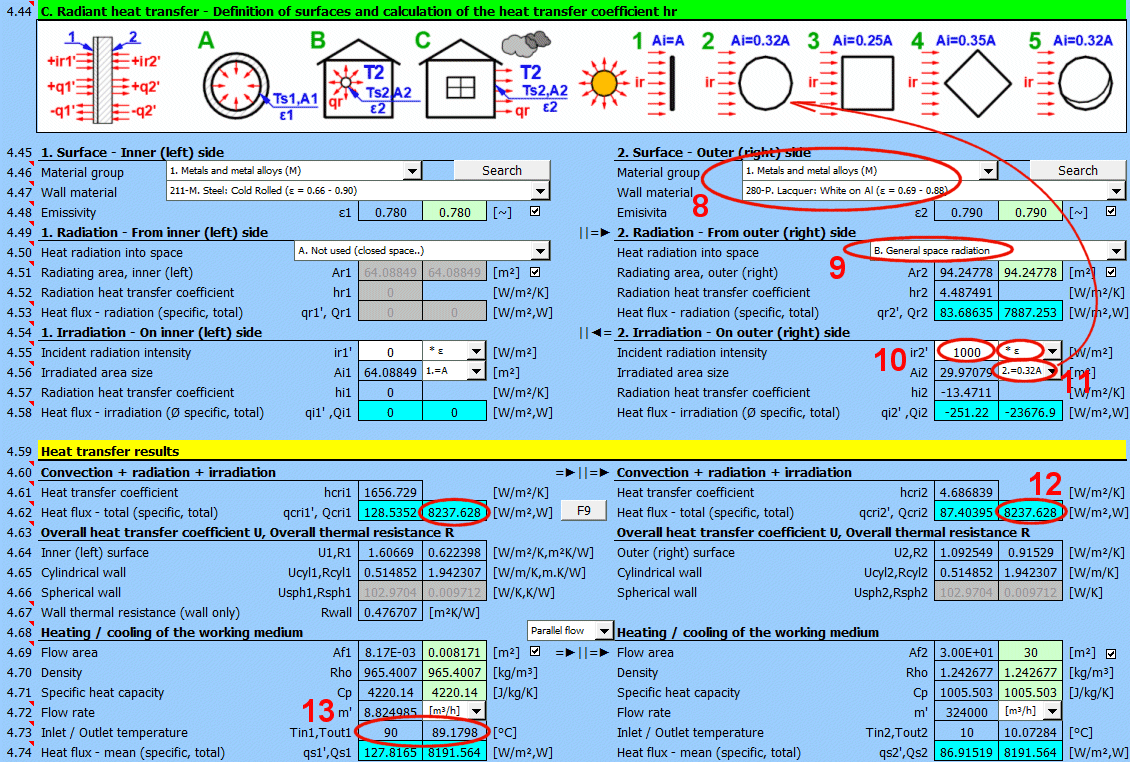
12. Die resultierenden Verluste betragen 8237 W.
13. Die Temperatur am Rohrende beträgt ungefähr 89,2 °C.
Versuchen Sie, den Deckanstrich (Emissivität ε2 [4.47, 4.48]) sowohl für das sonnenbestrahlte Rohr als auch für das unbestrahlte Rohr (ir2 = 0 W/m^2 [4.51]) zu ändern.
1. Benennen Sie die aktuelle Wärmeübertragungslösung.
2. Fügen Sie eine Beschreibung der Lösung hinzu.
3. Fügen Sie die aktuelle Lösung der Liste auf dem Blatt "Wände" hinzu.
4. Wählen Sie eine Lösung aus der Liste der gespeicherten Lösungen.
5. Laden Sie die vollständigen Daten. Die aktuellen Werte werden durch die Werte
der ausgewählten Lösung überschrieben.

Die Lösungen werden im Blatt "Wände" gespeichert. Eine Zeile enthält eine
gespeicherte Lösung.
Das Blatt "Wände" ist frei zugänglich und kann mit den Excel-Mitteln (z.B.
Löschen nicht benötigter Lösungen - Zeilen) normal bearbeitet werden.
Wenn Sie einen bestimmten Wert ermitteln und in Ihrer eigenen Formel verwenden möchten, steht die Funktion GetWallProp zur Verfügung.
Syntax:
GetWallProp(ID;value_name)
`ID` ... Zeilennummer auf dem Blatt "Wände", die die gespeicherte Lösung
enthält.
`value_name` ... Name des Wertes, den Sie ermitteln möchten.
Beispiel:
`=GetWallProp(1;"Date")` ... Gibt das Datum zurück, an dem die Lösung der Liste
hinzugefügt wurde.
`=GetWallProp(1;"T1")` ... Gibt die Temperatur des Mediums 1 - T1 in [°C]
zurück.
`=GetWallProp(1;"U1")` ... Gibt den Wert des Wärmeübergangskoeffizienten U1 in
[W/m²/K] zurück.
Eine häufige Aufgabe kann die Bestimmung von Wärmeübertragungsparametern sein, wenn Sie (z.B. aus Messungen) einige Werte kennen und die vollständige Wärmeübertragung durch die Wand nicht lösen möchten.
Die Temperatur einer 3,5 m hohen und 20 m langen Hausaußenwand wurde mit einer Wärmebildkamera mit T{s1=3 °C gemessen. Die Umgebungsluft hat eine Temperatur von T1=0 °C und strömt mit einer Geschwindigkeit von 3 m/s entlang der Wand.
Bestimmen Sie den Wärmeübergangskoeffizienten U und den gesamten Wärmestrom Q.
1. Geben Sie die Temperatur der strömenden Luft T1=0 °C ein (Temperatur T2
kann beliebig gewählt werden).
2. Wählen Sie eine ebene Wand.
3. Wählen Sie ein beliebiges Wandmaterial (dessen Parameter sind irrelevant).
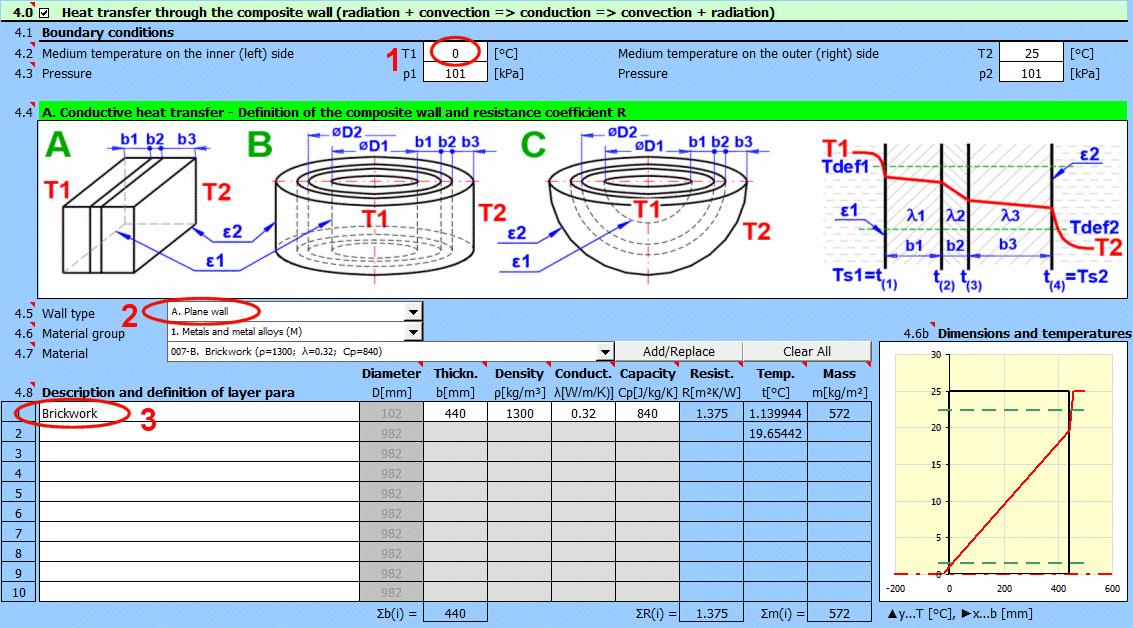
4. Wählen Sie Luft als Arbeitsmedium.
5. Deaktivieren Sie das automatische Ausfüllen der Wandtemperatur Ts1. Dadurch
wird die komplexe Berechnung unterbrochen und nur die linke Wandseite gelöst.
6. Geben Sie die Wandtemperatur Ts1=3 °C ein.
7. Wählen Sie erzwungene Strömung um eine ebene Fläche.
8. Geben Sie die Strömungsgeschwindigkeit v1=3 m/s ein.
9. Geben Sie die Abmessungen der Fläche ein.
10. Drücken Sie die Taste zur Iteration von hc1.
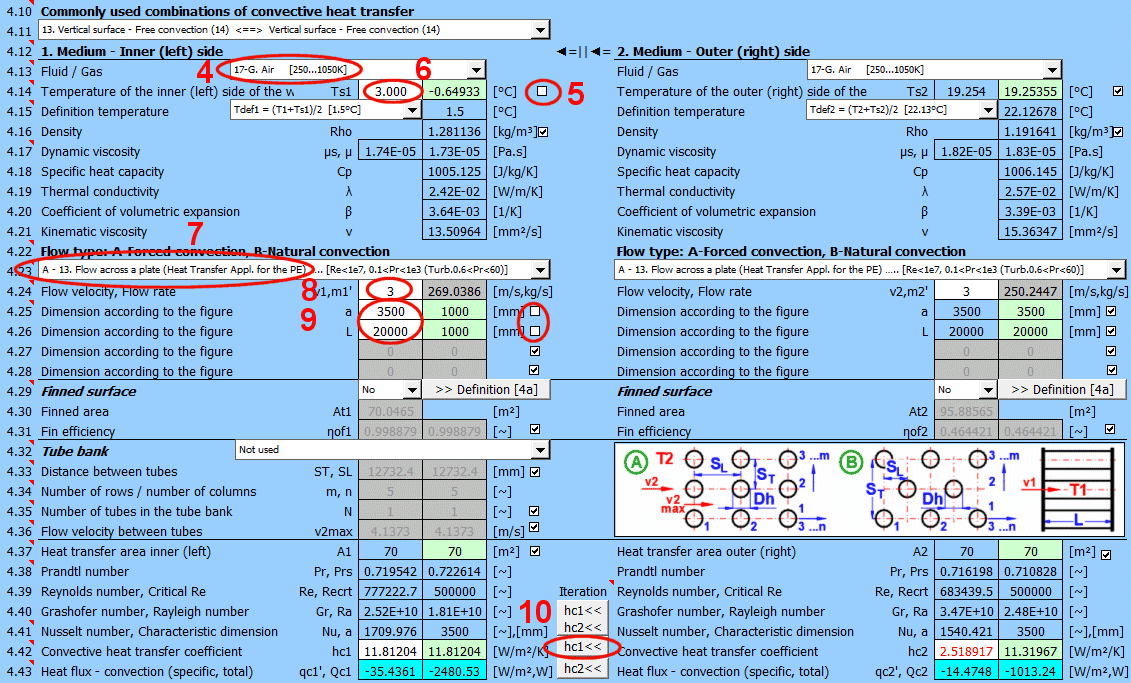
11. Wählen Sie das Oberflächenmaterial der Wand.
12. Oder geben Sie die Emissivität der Oberfläche direkt ein.
13. Wählen Sie die Wärmeabstrahlung im Freien.
14. Sie erhalten den gesamten Wärmestrom durch die Wand Q1 und den
Wärmeübergangskoeffizienten U1.
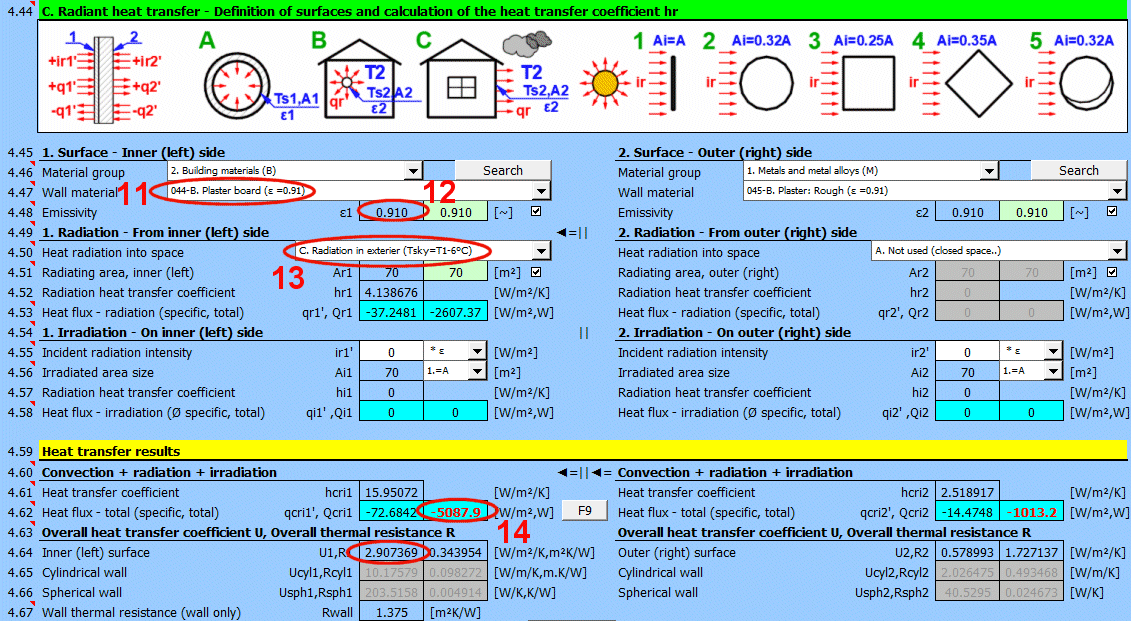
Versuchen Sie, den Deckanstrich (Emissivität ε2 [4.47, 4.48]) zu ändern.
Für verschiedene kryogene Behälter, Thermosflaschen usw. wird häufig eine Wand mit Vakuum auf einer Seite verwendet.
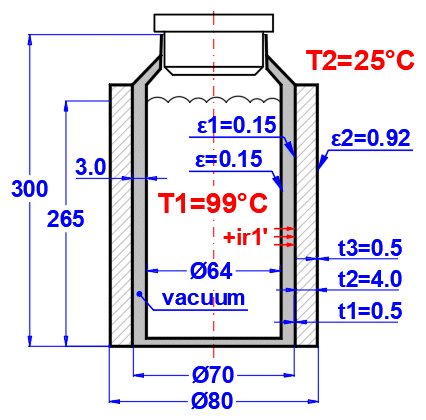
Eine Thermosflasche mit einem Volumen von 0,85 L hat eine zylindrische Wand, die aus 0,5 mm Stahlblech, 4,0 mm Isolierung und 0,5 mm PVC-Ummantelung besteht. Auf der Innenseite der Wand befindet sich ein Vakuum. Auf der Außenseite befindet sich Luft mit einer Temperatur von 25 °C. Die zylindrische Wand hat einen Innendurchmesser D=70 mm und eine Höhe L=300 mm. Im Inneren der Thermosflasche befindet sich ein Behälter mit Wasser bei einer Temperatur von 99 °C. Die Dicke des Vakuums beträgt 3 mm. Die Strahlung auf die Innenwand beträgt 45 W/m^2 (aus der Berechnung in Abschnitt [7.0]).
Bestimmen Sie den Wärmeübergangskoeffizienten U und den gesamten Wärmestrom Q.
Akzeptierte Vereinfachung: Es wird der Wärmeübergang der Umfangswand gelöst, der Einfluss des Bodens wird durch die Verwendung der Höhe von 300 mm kompensiert.
1. Geben Sie die Temperaturen T1=99 °C und T2=25 °C ein.
2. Wählen Sie eine zylindrische Wand.
3. Definieren Sie die einzelnen Wandschichten.
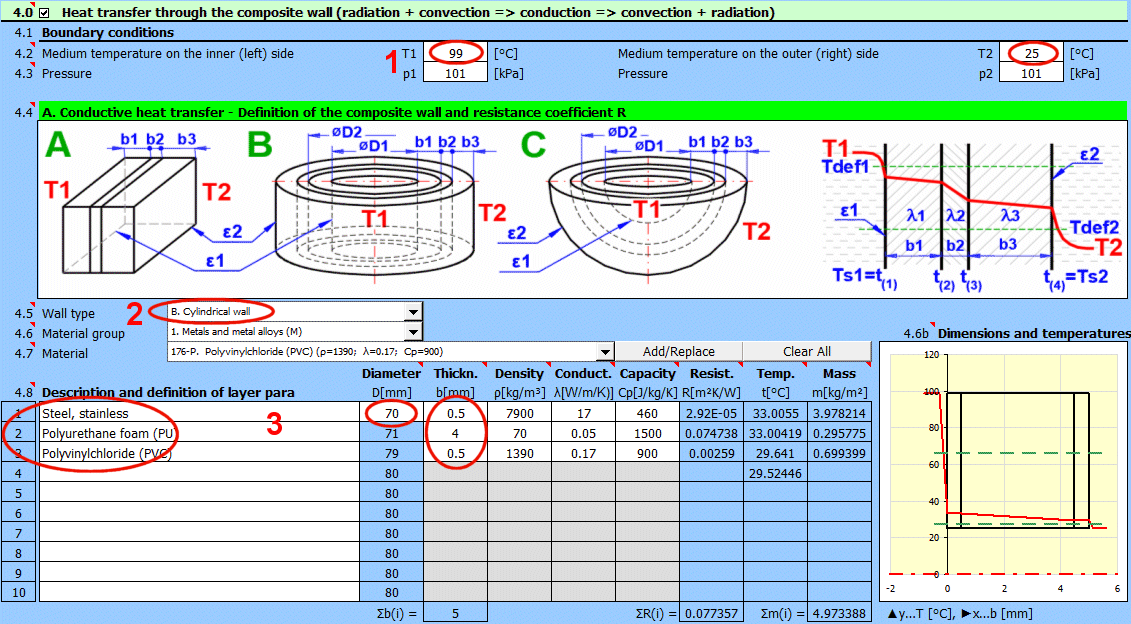

4. Wählen Sie die Arbeitsmedien 1 und 2.
5. Wählen Sie den Strömungstyp = Form der umströmten Fläche.
6. Geben Sie die Abmessungen des umströmten Behälters ein.
7. Drücken Sie die Taste für die schrittweise Iteration der Ergebnisse.
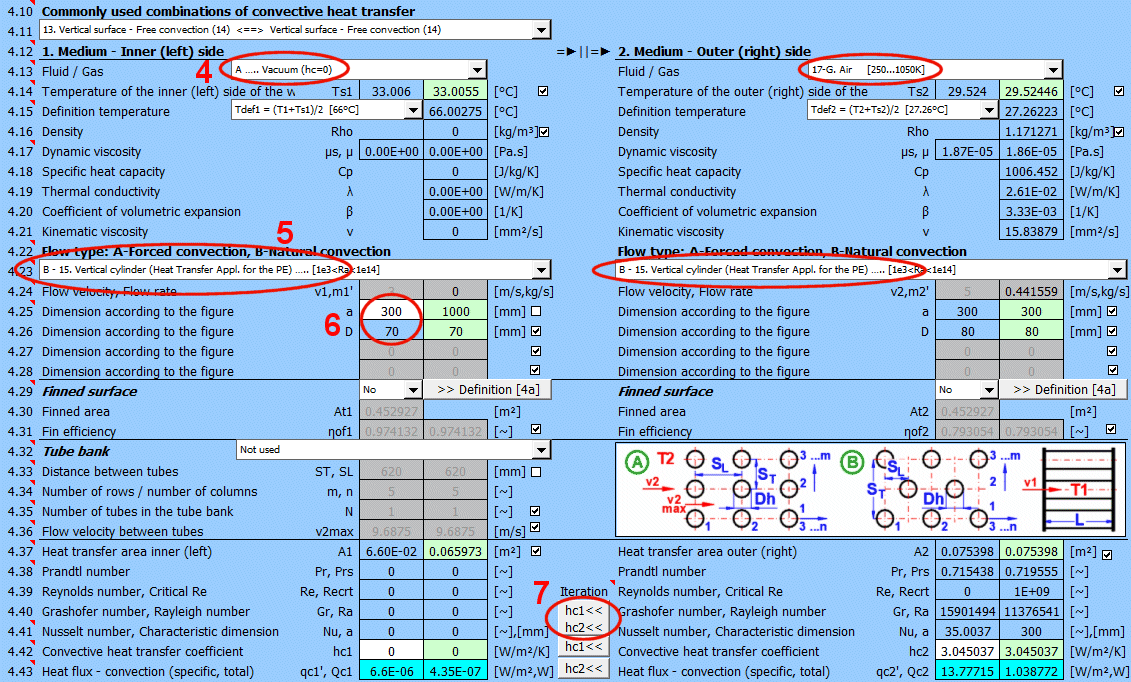
Es ist notwendig, die Abstrahlung in den Raum für die äußere Oberfläche zu
lösen.
8. Wählen Sie den Oberflächentyp oder geben Sie die Emissivität ε2=0,92 direkt
bei [4.45] ein.
9. Wählen Sie die Wärmeabstrahlung im Innenbereich.
Bestrahlung der inneren Wandoberfläche.
10. Die Abstrahlung in den Raum wird nicht gelöst - es wird ein geschlossener
Raum behandelt.
11. In Abschnitt [7.0] wird die Strahlungsgröße ir1=45 W/m^2 (Beispiel 18 unten)
für eine Wandemissivität ε1=0,15 berechnet, wählen Sie daher den Multiplikator
"* 1".
12. Die gesamte Innenfläche ist bestrahlt, wählen Sie die Option "1.=A".
13. Die Werte q, Q und U können in weiteren Berechnungen verwendet werden
(Beispiel 15 unten).
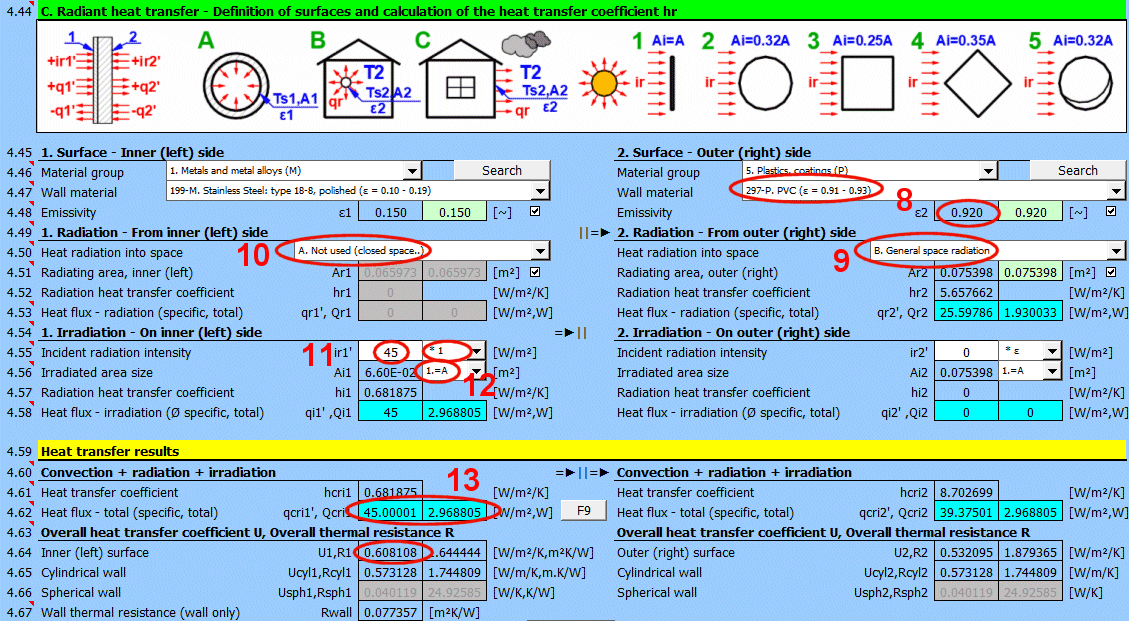
Analyse eines elektrischen Stromgenerators mit TEG-Modulen und einem luftgekühlten Kühler.
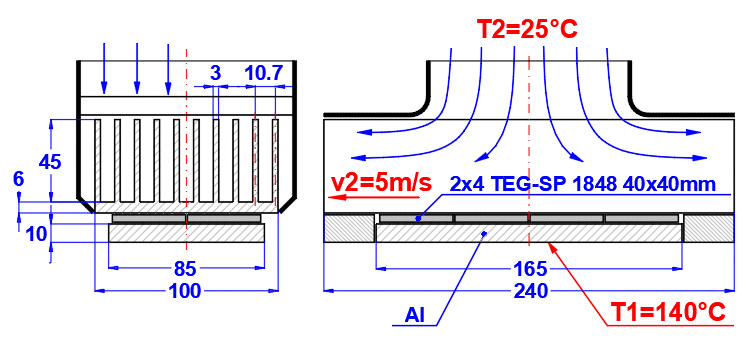
Acht TEG-Module liegen auf einer Seite an einer Aluminiumplatte mit den Abmessungen 85 x 165 x 10 mm an. Auf der anderen Seite liegen sie an einem Aluminiumkühler mit den Abmessungen 100 x 240 x 51 mm mit zehn Rippen und einer Grundplattenstärke von 6 mm an. Die Aluminiumplatte ist kontaktiert mit einer Wärmequelle mit einer Temperatur von T1=140 °C verbunden. Durch den Kühler strömt Luft mit einer Temperatur von T2=25 °C und einer Geschwindigkeit von 5 m/s. Die Wärmeleitfähigkeit des TEG-Moduls beträgt 1,5 [W/m/K].
Ermitteln Sie die Temperatur des TEG-Moduls auf der heißen und kalten Seite.
1. Geben Sie die Temperaturen T1=140 °C und T2=25 °C ein.
2. Wählen Sie eine ebene Wand.
3. Definieren Sie die einzelnen Wandschichten gemäß Abbildung.
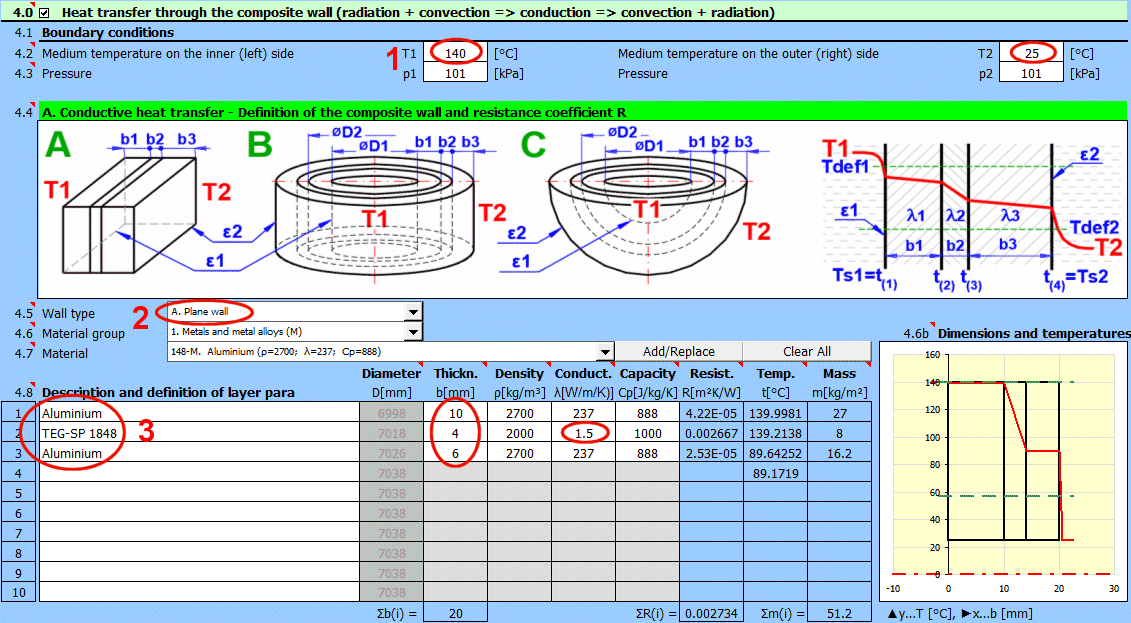

4. Wählen Sie die Arbeitsmedien 1 und 2 (Medium 1 - Kontaktverbindung zur
Wärmequelle).
5. Geben Sie die Abmessungen der Kontaktplatte ein.
6. Wählen Sie den Strömungstyp (Erzwungene Umströmung der Platte = Luftströmung
im Kühler).
7. Geben Sie die Abmessungen der Kühlergrundfläche und die
Luftströmungsgeschwindigkeit ein.
8. Aktivieren Sie die Verwendung einer gerippten Oberfläche und definieren Sie
deren Abmessungen in Abschnitt [4a.0].
9. Nach der Definition der Rippenabmessungen drücken Sie die Taste für die
schrittweise Iteration der Ergebnisse.
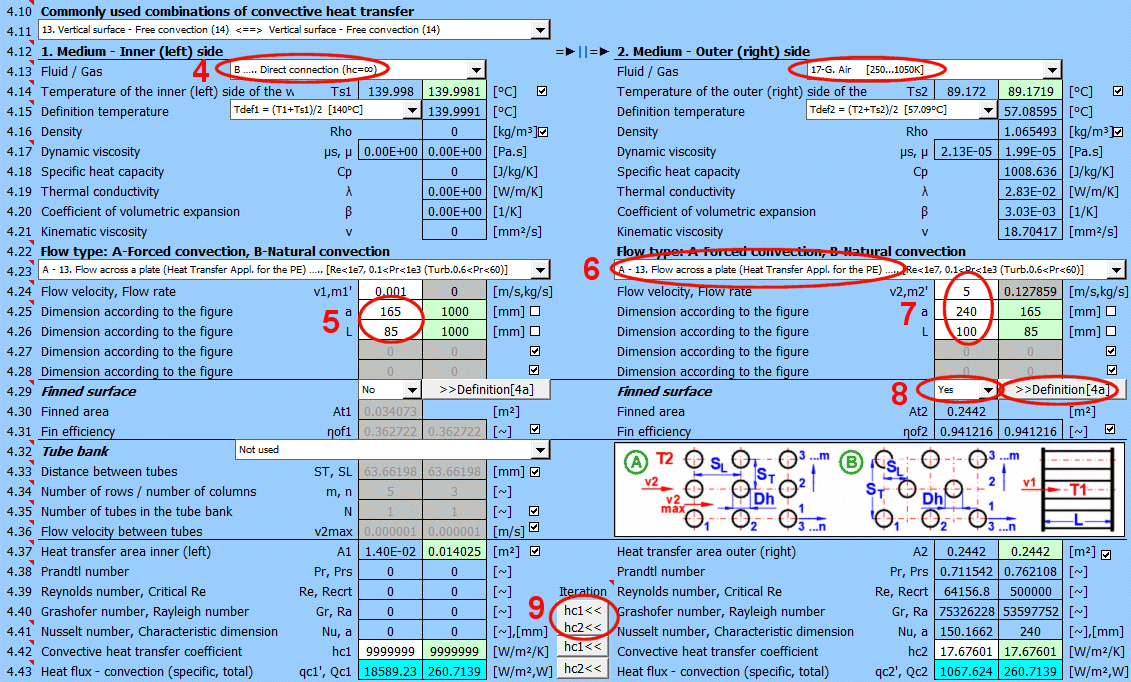
10. Wählen Sie die rechteckige Rippenform.
11. Geben Sie die Abmessungen und die Anzahl der Rippen ein. Die vorgeschlagene
Anzahl der Rippen wird aus der Breite des Rippenfeldes [4a.5] und den Abständen
zwischen den Rippen [4a.9] berechnet.
12. Der Wirkungsgrad der Rippen (verwendet zur Berechnung des
Wärmeübergangskoeffizienten [4.29, 4.39]) wird berechnet.
13. Die umströmte Fläche, die durch die Rippen vergrößert wird, wird berechnet
und anstelle des ursprünglichen Wertes [4.34] verwendet.
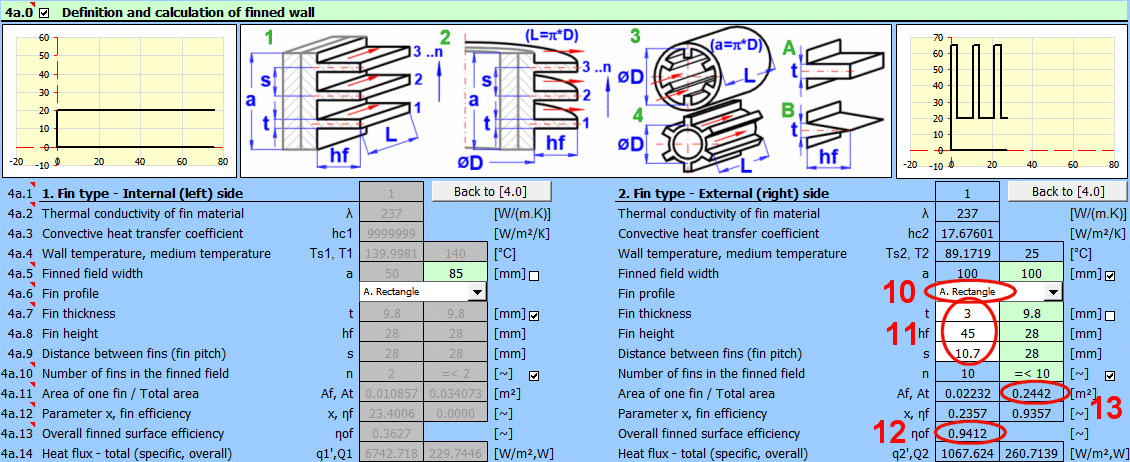
In dieser Berechnung muss keine Strahlung berücksichtigt werden, die Parameter müssen entsprechend eingestellt werden.
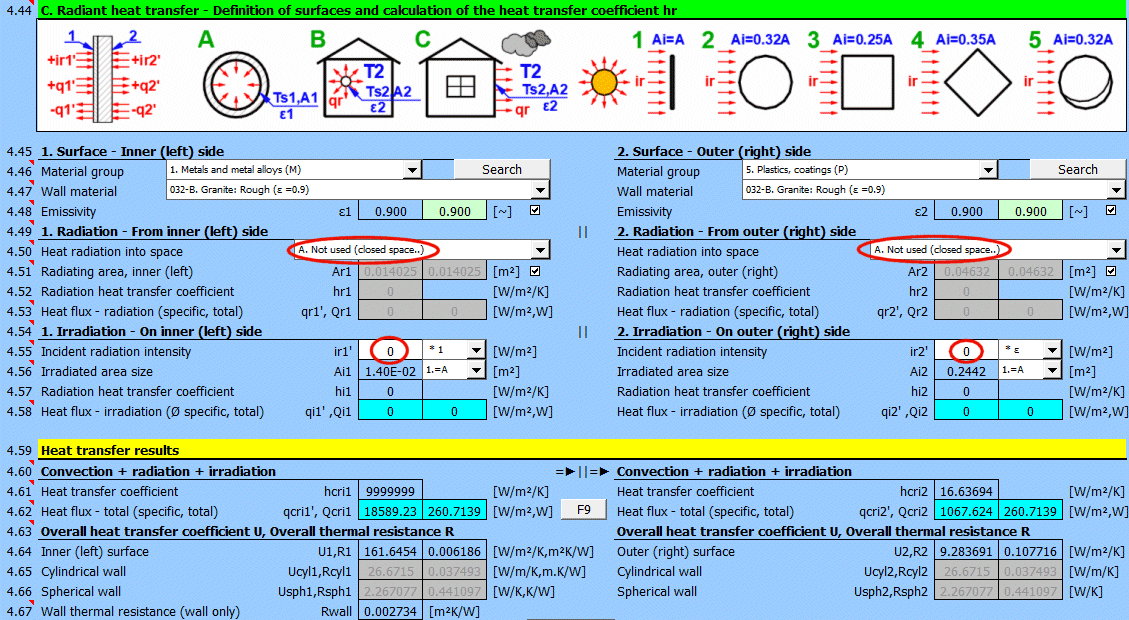
Die gewünschten Ergebnisse (Wandtemperaturen des TEG-Moduls) finden Sie in Tabelle [4.8].
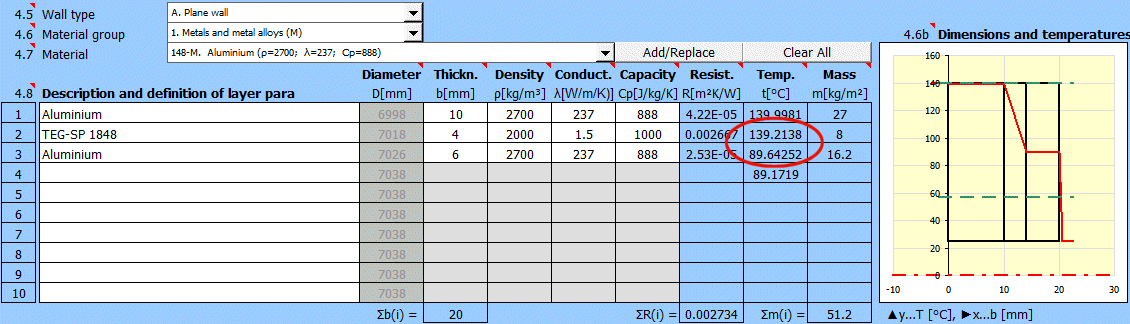
Fazit: Die Temperaturdifferenz beträgt 50 °C. Aus den Katalogangaben ergibt sich für diese Temperaturdifferenz eine Leistung eines einzelnen Moduls von etwa 1 W, für 8 Module also 8 W. Um die Temperaturdifferenz zu erhöhen, müsste die Kühlfläche wesentlich vergrößert werden (mehr dünnere und höhere Rippen) oder beispielsweise Wasserkühlung eingesetzt werden.
Berechnung des Wärmeübergangs in einem Rohrbündel.
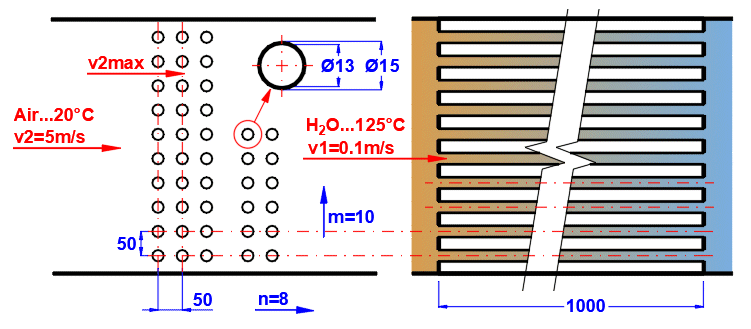
Wasser aus einer Geothermiebohrung mit einer Temperatur von T1=125 °C fließt mit einer Geschwindigkeit von 0,1 m/s durch die Rohre. Die Stahlrohre sind in einem Bündel von 10 Reihen und 8 Spalten angeordnet. Der Innendurchmesser des Rohres beträgt D1=13 mm, der Außendurchmesser D2=15 mm. Luft tritt mit einer Temperatur von T2=20 °C und einer Geschwindigkeit von 5 m/s in das Rohrbündel ein.
Bestimmen Sie die Austrittstemperatur der Luft und die Leistung des Wärmetauschers.
1. Geben Sie die Temperaturen T1=125 °C und T2=20 °C ein.
2. Wählen Sie eine zylindrische Wand.
3. Definieren Sie die Abmessungen und das Material des Rohres.
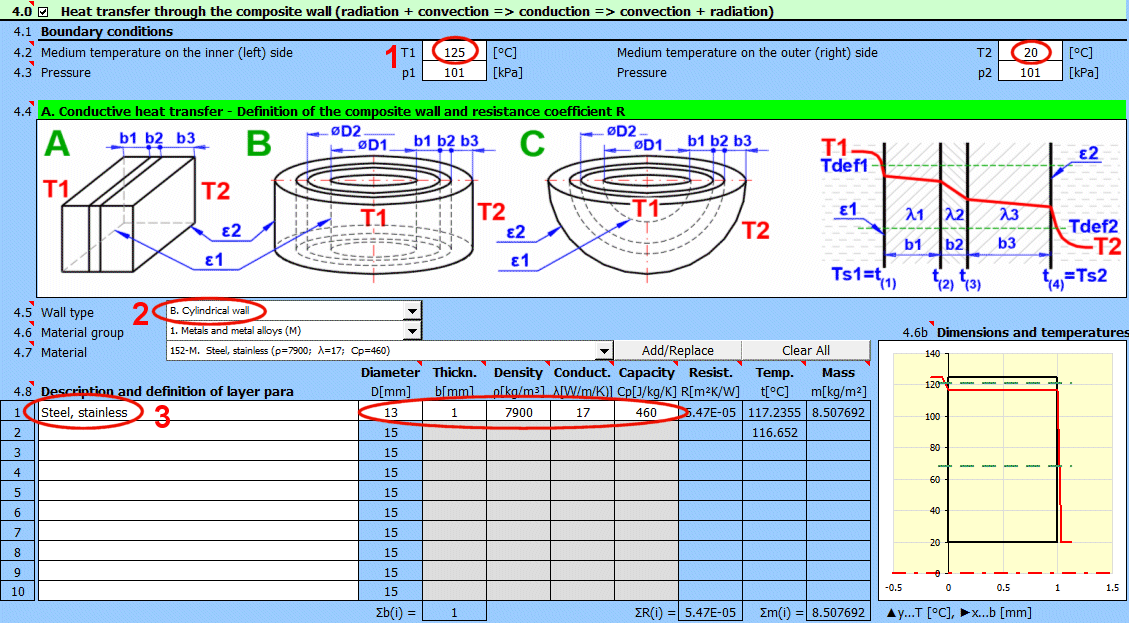

4. Wählen Sie die Arbeitsmedien 1 und 2.
5. Wählen Sie den Strömungstyp (Wasser fließt durch das Rohr, Luft umströmt das
Rohr).
6. Geben Sie die Strömungsgeschwindigkeiten und die inneren und äußeren
Rohrabmessungen ein.
7. Aktivieren und wählen Sie die Anordnung der Rohre im Bündel.
8. Geben Sie die Abstände zwischen den Rohren und deren Anzahl gemäß Abbildung
ein.
9. Nach der Definition der Abmessungen drücken Sie die Taste für die
schrittweise Iteration der Ergebnisse.
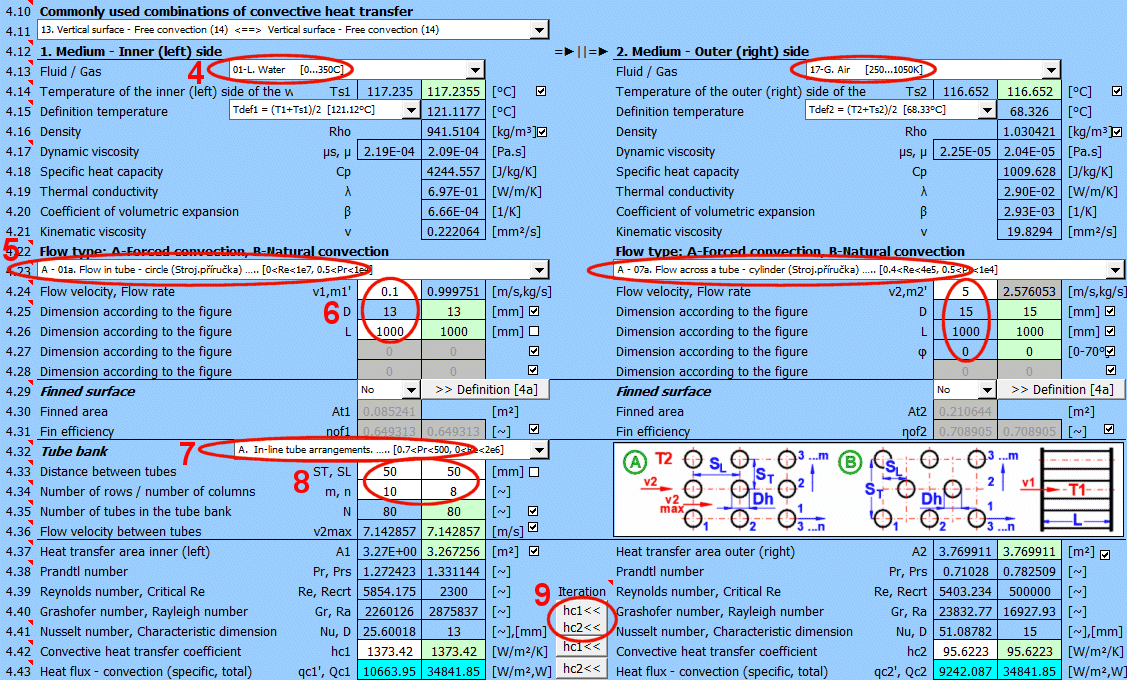
In dieser Berechnung muss keine Strahlung berücksichtigt werden, die Parameter müssen entsprechend eingestellt werden.
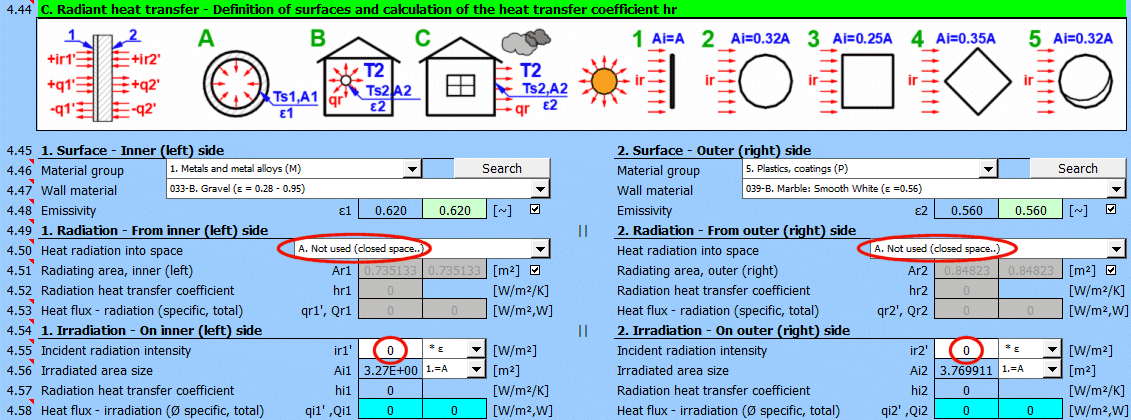
10. Wählen Sie den Typ der gegenseitigen Strömung - Gegenstrom (Weitere
Möglichkeiten finden Sie im Kapitel Wärmetauscher).
11. Wenn das Kontrollkästchen aktiviert ist, werden die voreingestellten Werte
Af, Rho, Cp verwendet. Das Programm versucht, sie basierend auf den oben
eingegebenen Werten vorzuschlagen.
12. Wenn Ihnen die voreingestellten Werte nicht zusagen, können Sie nach dem
Deaktivieren des Kontrollkästchens (11) eigene Werte eingeben.
13. Die Austrittstemperatur der Luft beträgt 30,5 °C und die Leistung knapp 32
kW.
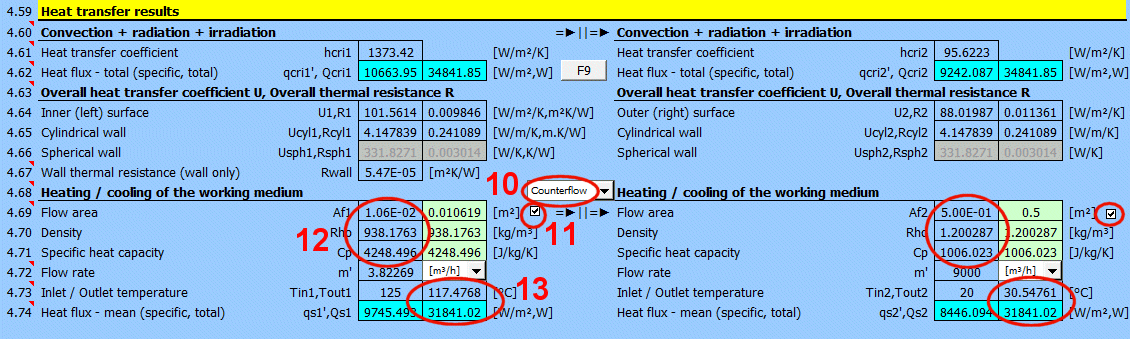
Fazit: Der Lufttemperaturanstieg von 10 °C ist relativ gering. Für einen Wasser-Luft-Wärmetauscher wäre eine Berippung eindeutig vorteilhafter.
Im vorherigen Beispiel wurden Rohre ohne Berippung verwendet. In diesem Beispiel verwenden wir weniger Rohre mit größeren Abmessungen und mit Berippung.
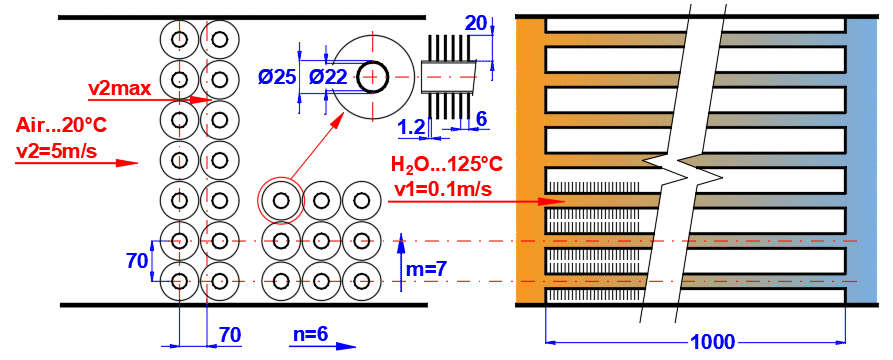
Wasser aus einer Geothermiebohrung mit einer Temperatur von T1=125 °C fließt mit einer Geschwindigkeit von 0,1 m/s durch die Rohre. Die Stahlrohre sind in einem Bündel von 7 Reihen und 6 Spalten angeordnet. Der Innendurchmesser des Rohres beträgt D1=22 mm, der Außendurchmesser D2=25 mm. Luft tritt mit einer Temperatur von T2=20 °C und einer Geschwindigkeit von 5 m/s in das Rohrbündel ein. Die Rohre sind mit Rippen versehen. Rippendicke t=1,2 mm, Rippenhöhe hf=20 mm und Abstand s=6 mm. Es wird die maximale Rippenanzahl n=167 verwendet.
Bestimmen Sie die Austrittstemperatur der Luft und die Leistung des Wärmetauschers.
1. Geben Sie die Temperaturen T1=125 °C und T2=20 °C ein.
2. Wählen Sie eine zylindrische Wand.
3. Definieren Sie die Abmessungen und das Material des Rohres.
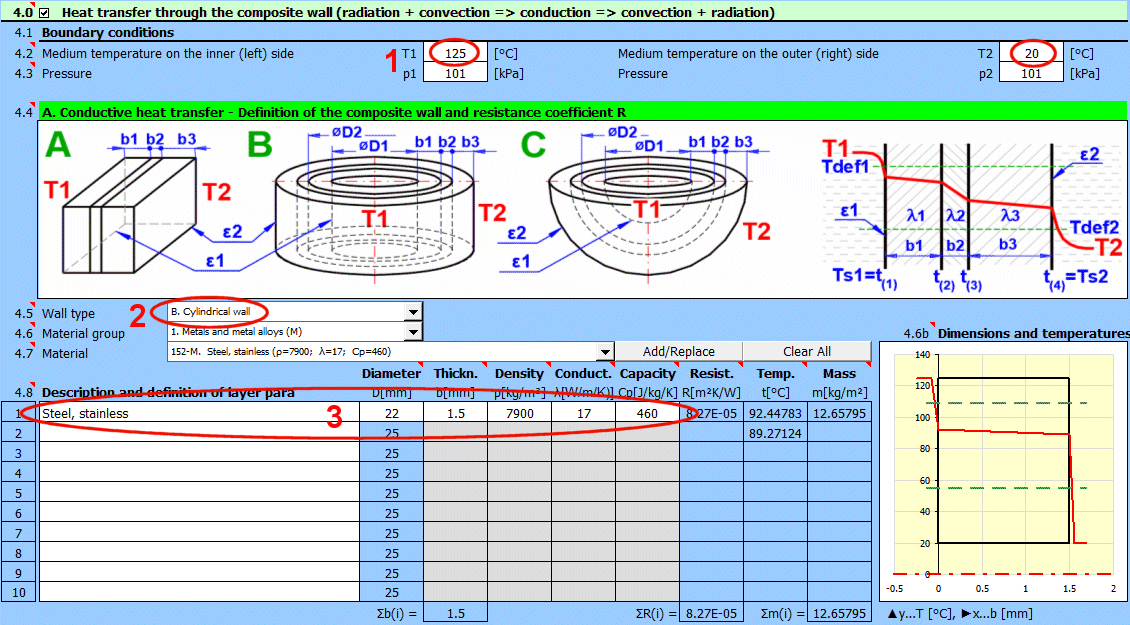

4. Wählen Sie die Arbeitsmedien 1 und 2.
5. Wählen Sie den Strömungstyp (Wasser fließt durch das Rohr, Luft umströmt das
Rohr).
6. Geben Sie die Strömungsgeschwindigkeiten und die inneren und äußeren
Rohrabmessungen ein.
7. Aktivieren Sie die Verwendung einer gerippten Oberfläche und definieren Sie
deren Abmessungen in Abschnitt [4a.0].
8. Aktivieren und wählen Sie die Anordnung der Rohre im Bündel.
9. Geben Sie die Abstände zwischen den Rohren und deren Anzahl gemäß Abbildung
ein.
10. Nach der Definition der Abmessungen drücken Sie die Taste für die
schrittweise Iteration der Ergebnisse.
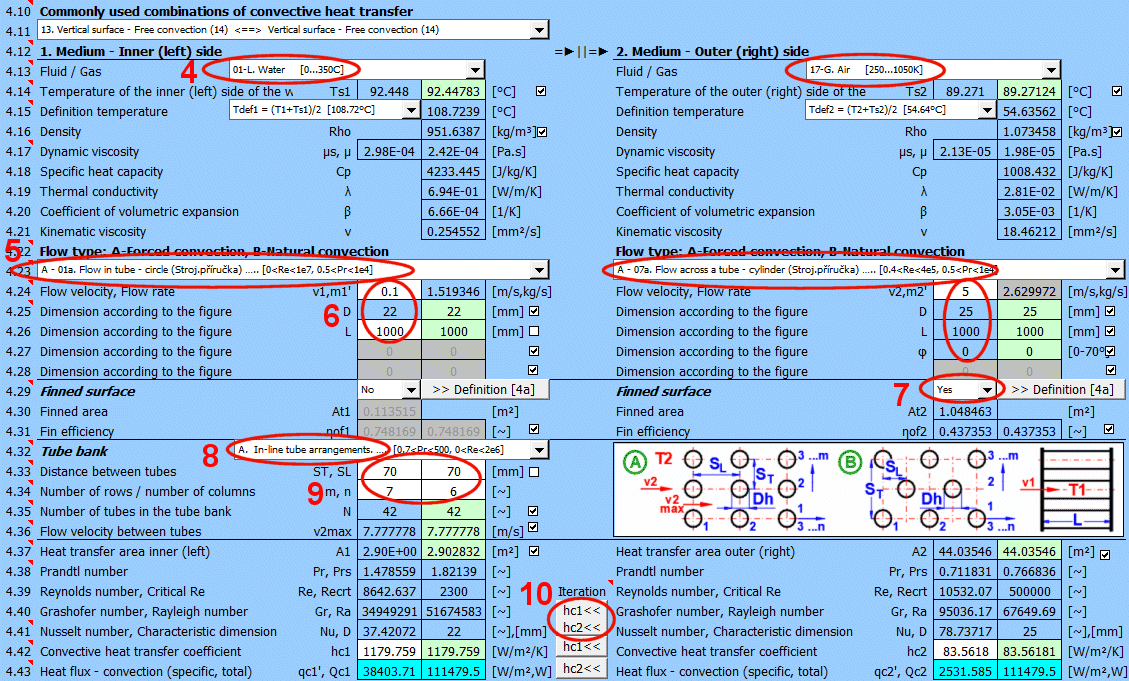
11. Wählen Sie die rechteckige Rippenform.
12. Geben Sie die Abmessungen und die Anzahl der Rippen ein. Die vorgeschlagene
Anzahl der Rippen wird aus der Breite des Rippenfeldes [4a.5] und den Abständen
zwischen den Rippen [4a.9] berechnet.
13. Der Wirkungsgrad der Rippen (verwendet zur Berechnung des
Wärmeübergangskoeffizienten [4.29, 4.39]) wird berechnet.
14. Die umströmte Fläche, die durch die Rippen vergrößert wird, wird berechnet
und anstelle des ursprünglichen Wertes [4.34] verwendet.
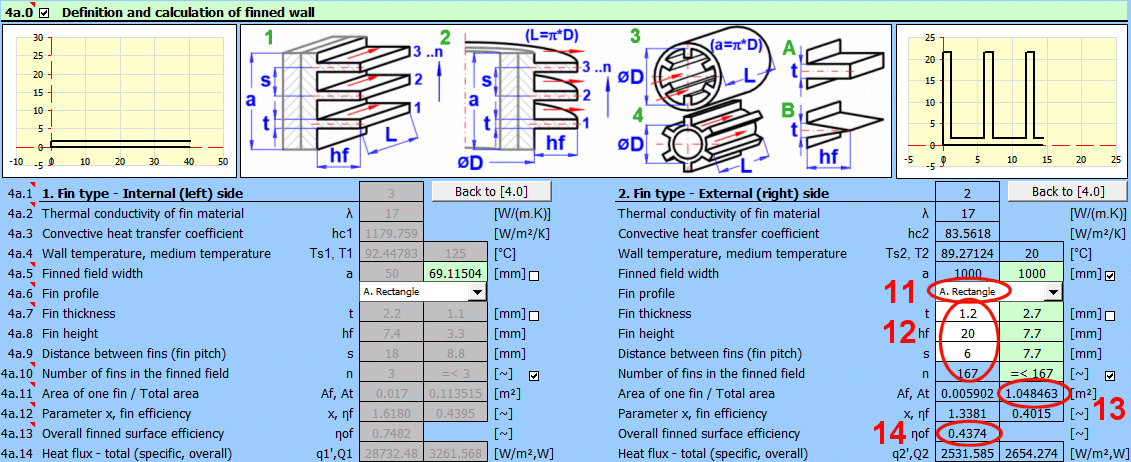
In dieser Berechnung muss keine Strahlung berücksichtigt werden, die Parameter müssen entsprechend eingestellt werden.
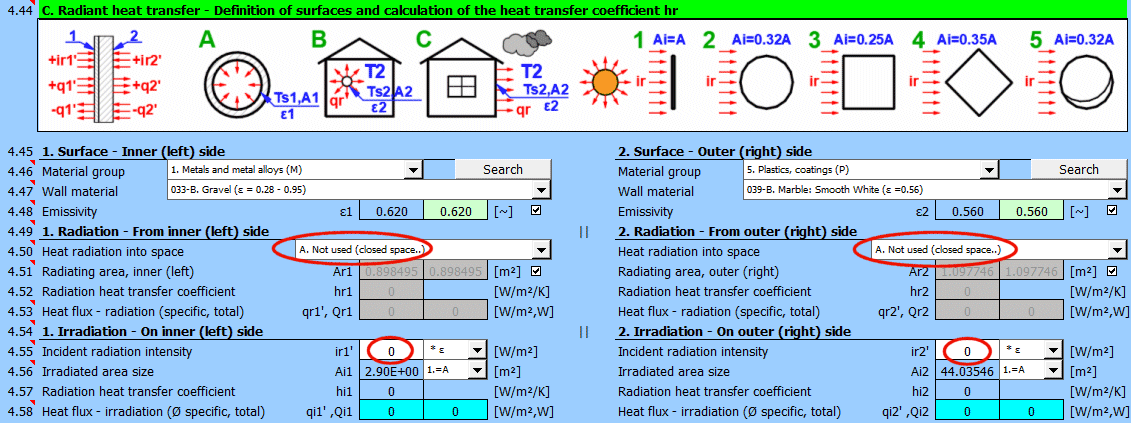
15. Wählen Sie den Typ der gegenseitigen Strömung - Gegenstrom (Weitere
Möglichkeiten finden Sie im Kapitel Wärmetauscher).
16. Wenn das Kontrollkästchen aktiviert ist, werden die voreingestellten Werte
Af, \rho, Cp verwendet. Das Programm versucht, sie basierend auf den oben
eingegebenen Werten vorzuschlagen.
17. Wenn Ihnen die voreingestellten Werte nicht zusagen, können Sie nach dem
Deaktivieren des Kontrollkästchens (16) eigene Werte eingeben.
18. Die Austrittstemperatur der Luft beträgt 49,8 °C und die Leistung 88 kW
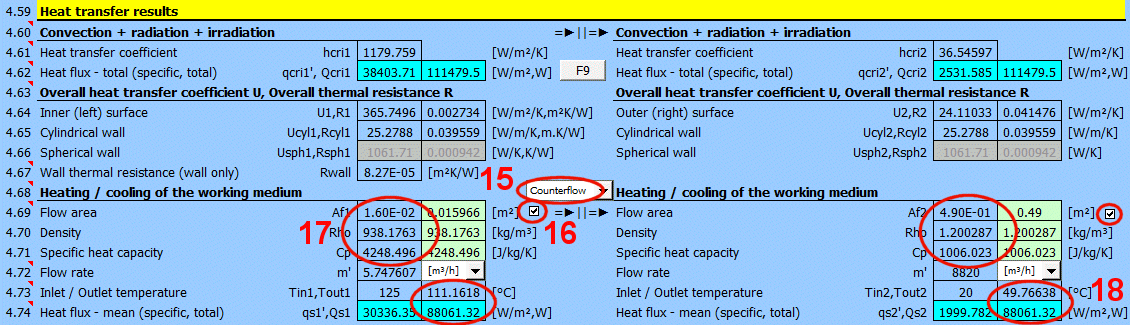
Fazit: Die Lufttemperaturerhöhung von 30 °C ist gegenüber dem vorherigen Beispiel dreifach, bei der halben Anzahl von Rohren.
Aus Beispiel 11 kennen wir den Wärmeübergangskoeffizienten U=0,6081 [W/m²/K] und die innere Fläche A=0,0659 [m²]. Die Anfangstemperatur der Flüssigkeit (Wasser) T1s=99 °C. Die Umgebungstemperatur T2=25 °C. Die Masse der Flüssigkeit beträgt 0,85 kg.

Bestimmen Sie die Abkühlzeit der Flüssigkeit von der Temperatur T1s=99 °C auf die Temperatur T1e=39 °C.
1. Wählen Sie die Flüssigkeit aus der Liste. Wenn die Flüssigkeit nicht in
der Liste ist, deaktivieren Sie das Kontrollkästchen und geben Sie den Wert für
Cp ein.
2. Aktivieren / Deaktivieren Sie das Kontrollkästchen. Bei Aktivierung werden
die aktuellen Werte aus Abschnitt [4.0] verwendet.
3. Füllen Sie die gewünschten Eingabewerte aus.
4. Die Abkühlzeit auf 39 °C beträgt 41,5 Stunden. Dies entspricht den
Benutzertests von Thermosflaschen der mittleren Preisklasse.
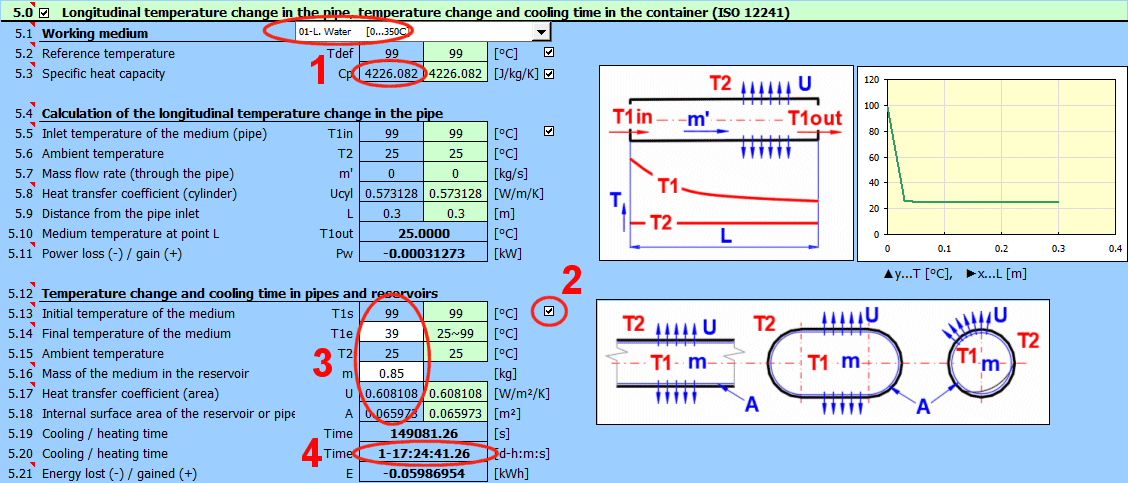
Zur Ölkühung wird ein Rohrbündelwärmetauscher verwendet. Der Massenstrom des Kühlwassers im Innenrohr beträgt m1'=0,25 kg/s, der Massenstrom des Öls im äußeren Ringspalt beträgt m2'=0,15 kg/s. Wasser tritt mit einer Temperatur von T1in=20 °C in den Wärmetauscher ein, Öl mit einer Temperatur von T2in=98 °C. Der Wärmeübergangskoeffizient für die zylindrische Wand beträgt 3,25 W/m/K.
Eine Ölausgangstemperatur von T2Out=62 °C wird gefordert. Bestimmen Sie die Wasserausgangstemperatur und die Länge des Wärmetauschers für einen Gegenstrom-Rohrbündelwärmetauscher.
Tipp: Ein Berechnungsbeispiel für geeignete Rohre und den Wärmeübergangskoeffizienten ist unter dem Namen Example16.... gespeichert und kann in die Berechnung geladen werden.
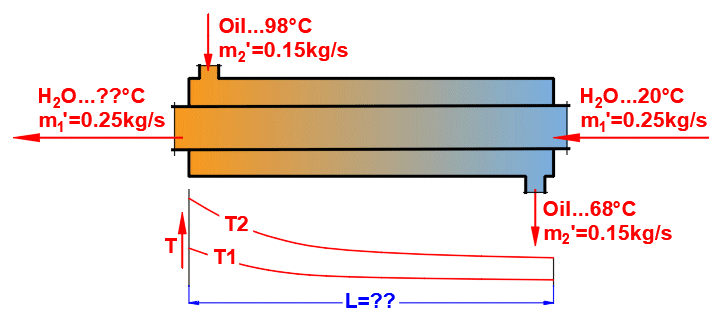

1. Wählen Sie den Wärmetauschertyp.
2. Wenn Sie sich entscheiden, Daten aus der Wanddefinition in Abschnitt [4.0] zu
laden, wählen Sie die entsprechende Definition aus und laden Sie mit der Taste
"Load".
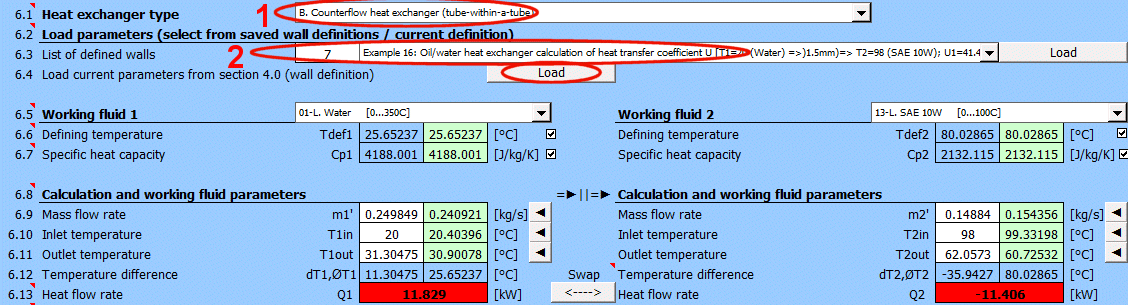
3. Wählen Sie die Arbeitsmedien 1 und 2. Wenn nicht in der Liste, geben Sie den
Wert für Cp direkt ein [6.7].
4. Geben Sie die Parameter für Medium 1 ein.
5. Geben Sie die Parameter für Medium 2 ein.
Die Werte Q1 und Q2 [6.13] werden höchstwahrscheinlich unterschiedlich und rot
markiert sein. Es ist notwendig, die Energiebilanz zu lösen. In den grünen
Feldern sind die berechneten Werte, die bei Anwendung sicherstellen, dass
Q1=-Q2.
6. Drücken Sie die Taste, mit der Sie den Vorschlagswert nach T1Out übertragen.
Die Austrittstemperatur des Wassers T1Out=31 °C.
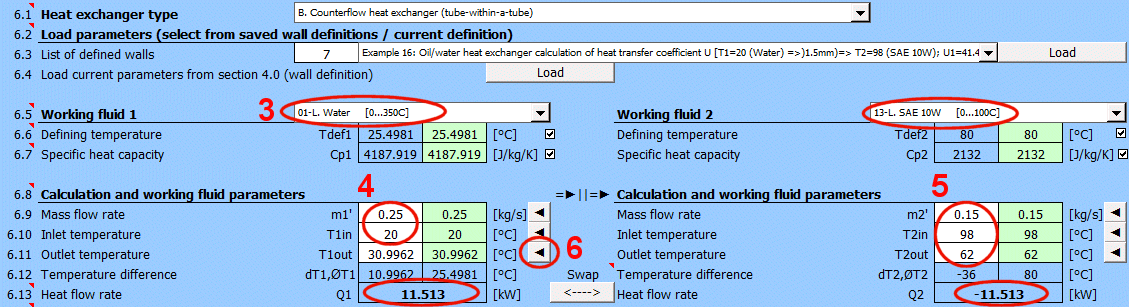
Nach Lösung der Energiebilanz kann die Rohrlänge (oder Fläche) berechnet werden.
7. Wählen Sie den Berechnungstyp B. In diesem Fall berechnen Sie die Länge des
Wärmetauschers und kennen Ucyl [W/m/K].
8. Geben Sie den Wert des Wärmeübergangskoeffizienten für das Rohr Ucyl ein.
Wenn Sie Werte aus der Wandberechnung (2) geladen haben, ist dieser Wert im
grünen Feld.
9. Das Ergebnis der Längenberechnung ist L=66 m.
10. Wenn Sie den Rohrdurchmesser kennen, können Sie die Länge in die Größe der
Wärmeübertragungsfläche umrechnen.
11. Wenn Sie die Verschmutzung des Wärmetauschers während des Betriebs in die
Berechnung einbeziehen möchten, geben Sie den Verschmutzungsfaktor Rf ein und
reduzieren Sie den Wert von Ucyl [6.21] um 4% [6.36].
12. Mit der Taste "▲U" stellen Sie den korrigierten Wert für Ucyl ein. Die
Rohrlänge für den Wärmetauscher einschließlich Verschmutzung beträgt dann L=69
m.
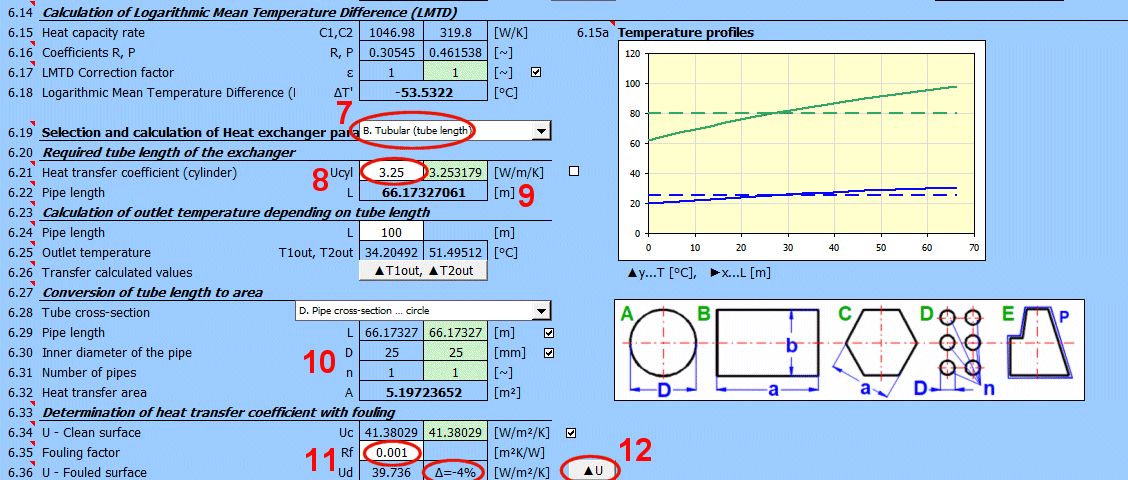
Wasserkühlung in einem Automobilkühler. Der Kühler besteht aus 40 Rohren mit
einem Innendurchmesser D1=5 mm und einer Länge L=650 mm, die durch dicht
angeordnete dünne Platten verlaufen.
Das in den Wärmetauscher eintretende Wasser hat eine Temperatur T1in=90 °C und
eine Austrittstemperatur T1Out=65 °C. Der Wasserdurchfluss beträgt m1'=0,6 kg/s.
Luft tritt mit T2in=20 °C in den Wärmetauscher ein und hat eine
Austrittstemperatur T2Out=40 °C.
Berechnen Sie den Luftdurchfluss durch den Wärmetauscher m2'=??, die Leistung Q=?? und den Wärmeübergangskoeffizienten U=??, der erreicht werden muss, um die Abmessungsanforderung von 40 Rohren mit einer Länge von 650 mm zu erfüllen.
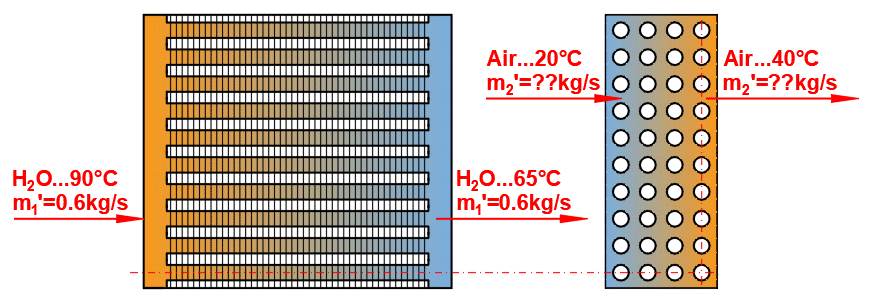

1. Wählen Sie den Wärmetauschertyp.
2. Wenn Sie sich entscheiden, Daten aus der Wanddefinition in Abschnitt [4.0] zu
laden, wählen Sie die entsprechende Definition aus und laden Sie mit der Taste
"Load".
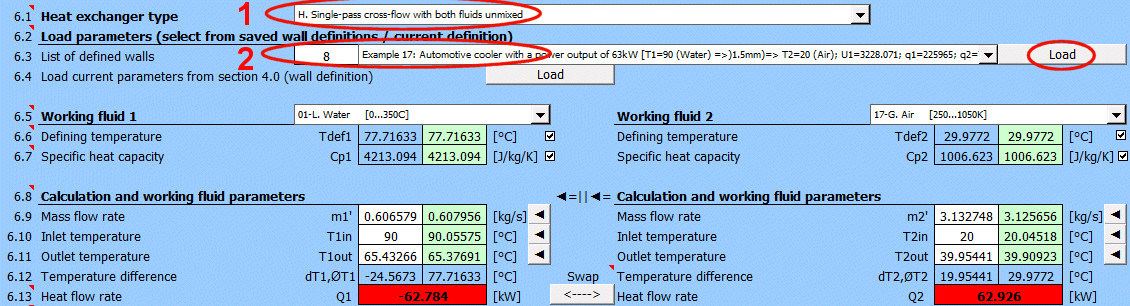
3. Wählen Sie die Arbeitsmedien 1 und 2. Wenn nicht in der Liste, geben Sie den
Wert für Cp direkt ein [6.7].
4. Geben Sie die Parameter für Medium 1 ein.
5. Geben Sie die Parameter für Medium 2 ein.
Die Werte Q1 und Q2 [6.13] werden höchstwahrscheinlich unterschiedlich und rot
markiert sein. Es ist notwendig, die Energiebilanz zu lösen. In den grünen
Feldern sind die berechneten Werte, die bei Anwendung sicherstellen, dass
Q1=-Q2.
6. Drücken Sie die Taste, mit der Sie den Vorschlagswert nach m2' übertragen.
Der Durchfluss der Kühlluft m2'=3,14 kg/s.
Die Kühlleistung des Radiators beträgt 63 kW.
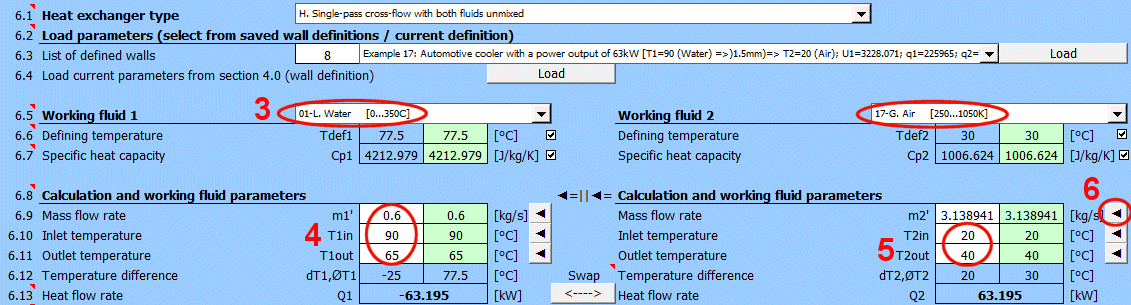
Nach Lösung der Energiebilanz kann der erforderliche Wärmeübergangskoeffizient
berechnet werden. Dies kann entweder der flächenbezogene Upl [W/m²/K], bezogen
auf die innere Rohrfläche, oder der längenbezogene Koeffizient Ucyl [W/m/K]
sein. In diesem Fall wählen wir die flächenbezogene Lösung (A).
Flächenberechnung. A = D1 * 3,14159 * L * n = 0,005 * 3,14159 * 0,65 * 40 =
0,4084 m^2.
7. Für Wärmetauscher vom Typ C-H muss ein Korrekturkoeffizient ε verwendet
werden. Der Koeffizient wird automatisch aus den Ein- und Austrittstemperaturen
vorgeschlagen.
8. Wählen Sie den Berechnungstyp A. In diesem Fall muss Upl [W/m²/K] bestimmt
werden, um die definierte Fläche A zu erreichen.
9. Ändern Sie den Wert von Upl schrittweise, bis die entsprechende Fläche A =
0,4084 m^2 erreicht ist.
10. Die korrekte Größe kann durch Umrechnung der Fläche A in die Rohrlänge
überprüft werden.
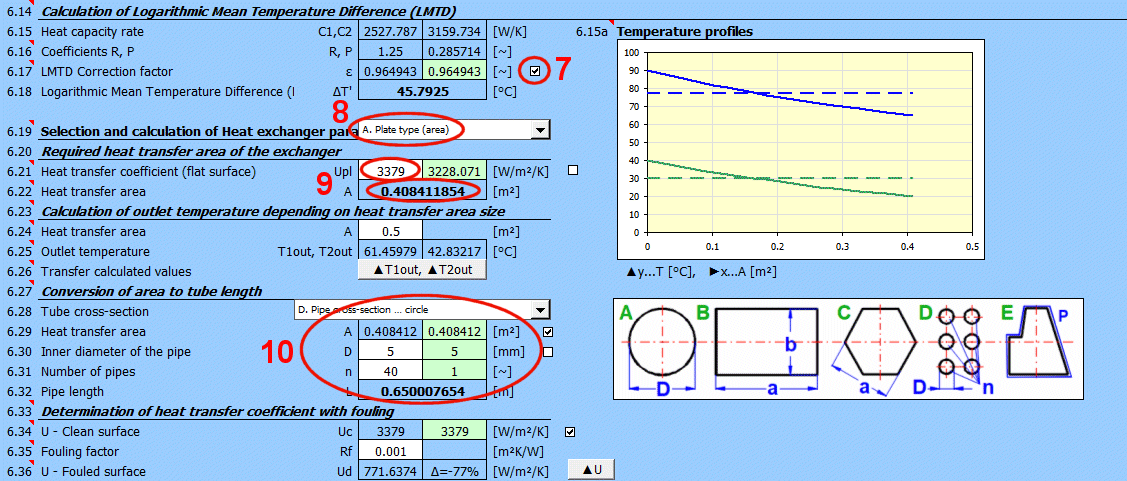
In Beispiel 11 müssen wir den gegenseitigen Wärmestrom zwischen zwei konzentrischen Zylindern bestimmen, zwischen denen sich ein Vakuum befindet. Die Wandtemperatur des inneren Zylinders beträgt T1=99 °C, die Wandtemperatur des äußeren Zylinders wird auf T2=30 °C geschätzt.

Bestimmen Sie den spezifischen Wärmestrom q21, der für die Lösung von Beispiel 11 erforderlich ist.
1. Wählen Sie zwei parallele Flächen.
2. Wählen Sie den Oberflächentyp oder geben Sie die Emissivität ε1=ε2=0,15
direkt bei [7.5] ein.
3. Geben Sie die Temperatur T1=99 °C ein.
4. Geben Sie die Temperatur T2=30 °C ein (erste Schätzung).
5. Geben Sie die Abmessungen der zylindrischen Flächen ein.
6. Der resultierende spezifische Wärmestrom q21=47 [W/m²].
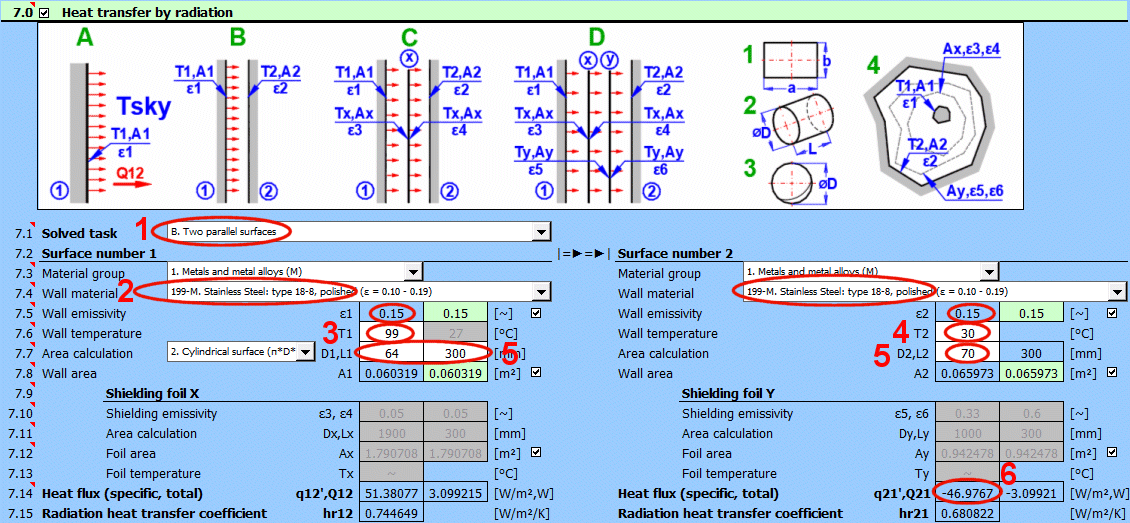
Nach dem Einsetzen des Wertes q21=47 [W/m²] in die Berechnung des
Wärmeübergangs durch die Wand in Abschnitt [4.0] ermitteln wir die genaue
Wandtemperatur T2=33 °C.
Nach dem erneuten Einsetzen von T2=33 °C in diese Berechnung erhalten wir einen
genaueren Wert q21=45 [W/m²].
Ein Rohr mit einem Durchmesser D1=200 mm, einer Oberflächentemperatur T1=200
°C und einer Emissivität ε1=0,93 ist konzentrisch in einem kreisförmigen Tunnel
mit einem Durchmesser D2=2000 mm, einer Oberflächentemperatur T2=20 °C und einer
Emissivität ε2=0,736 angeordnet. Die Abschirmung zwischen den Flächen erfolgt
durch eine dünne Aluminiumfolie, die konzentrisch angeordnet ist und eine
Emissivität ε3=ε4=0,05 aufweist. Bestimmen Sie den Wärmestrom zwischen dem Rohr
und dem Tunnel pro 1 m seiner Länge.
A) Ohne Abschirmung.
B) Die Abschirmfolie hat einen Durchmesser Dx=300 mm.
C) Die Abschirmfolie hat einen Durchmesser Dx=1900 mm.

1. Wählen Sie den Typ der zu lösenden Aufgabe.
2. Geben Sie die Emissivität der Oberflächen 1 und 2 ein.
3. Wählen Sie den Typ der zu lösenden Fläche.
4. Geben Sie die Temperatur und Abmessungen der Fläche 1 (Rohr) ein. Geben Sie
die Länge 1 m ein.
5. Geben Sie die Temperatur und den Durchmesser des kreisförmigen Tunnels ein
(Länge ist gleich).
6. Wärmestrom pro 1 m Rohr Q=1370 W.
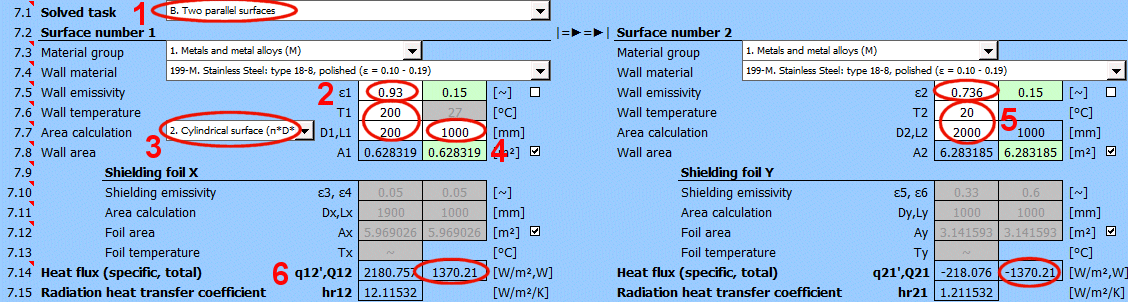
Die Werte für Wand 1 und 2 bleiben gleich.
1. Ändern Sie den Typ der zu lösenden Aufgabe auf C.
2. Geben Sie die Emissivität der Folie ε3, ε4 ein.
3. Geben Sie den Durchmesser der Abschirmfolie Dx=300 mm ein.
4. Wärmestrom pro 1 m Rohr Q=56 W.
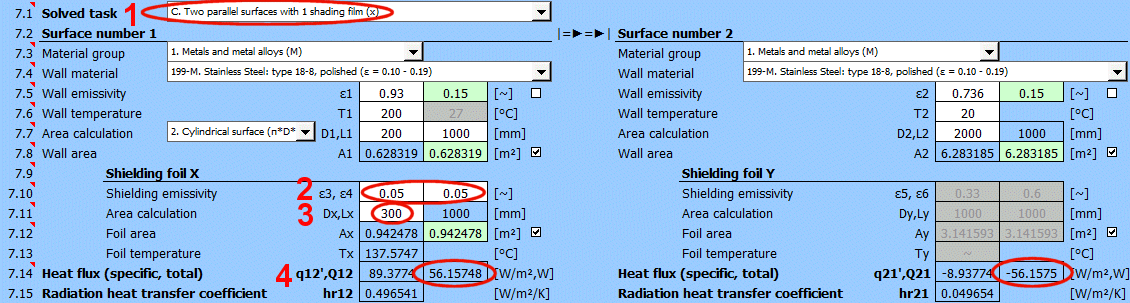
Die Werte für Wand 1 und 2 bleiben gleich, nur der Durchmesser Dx ändert
sich.
1. Geben Sie den Durchmesser der Abschirmfolie Dx=1900 mm ein.
6. Wärmestrom pro 1 m Rohr Q=292 W.

Fazit: Die Verwendung von Abschirmfolie kann ein wirksames Mittel zur Reduzierung der Wärmeübertragung sein.
Sie projektieren eine Rohrleitung, durch die Kühlflüssigkeit strömen wird. Ihr Standort befindet sich in der Nähe von Paris in einem Industriegebiet. Sie müssen die maximale solare Wärmestrahlung und den gesamten täglichen Energieeintrag ermitteln.
1. Die maximale Intensität der Sonnenstrahlung ist am 21. Juni um 12:00 Uhr.
2. Die geografische Breite von Paris beträgt \zeta = 48,9 °.
3. Stellen Sie die Neigung der Fläche senkrecht zur Sonne \beta=30 ° ein.
4. Stellen Sie die Ausrichtung der Fläche nach Süden \gamma=0 ° ein.
5. Die Höhe über dem Meeresspiegel von Paris beträgt Alt=35 m.
6. Luftverschmutzungsfaktor im Industriegebiet Z=5.
7. Maximale Sonnenstrahlungsintensität für einen klaren Himmel unter den
gewählten Bedingungen.
8. Gesamter täglicher Energieeintrag auf eine definierte ebene Fläche (an Punkt
3 und 4). Der Energieeintrag auf eine zylindrische Fläche ist etwas größer.
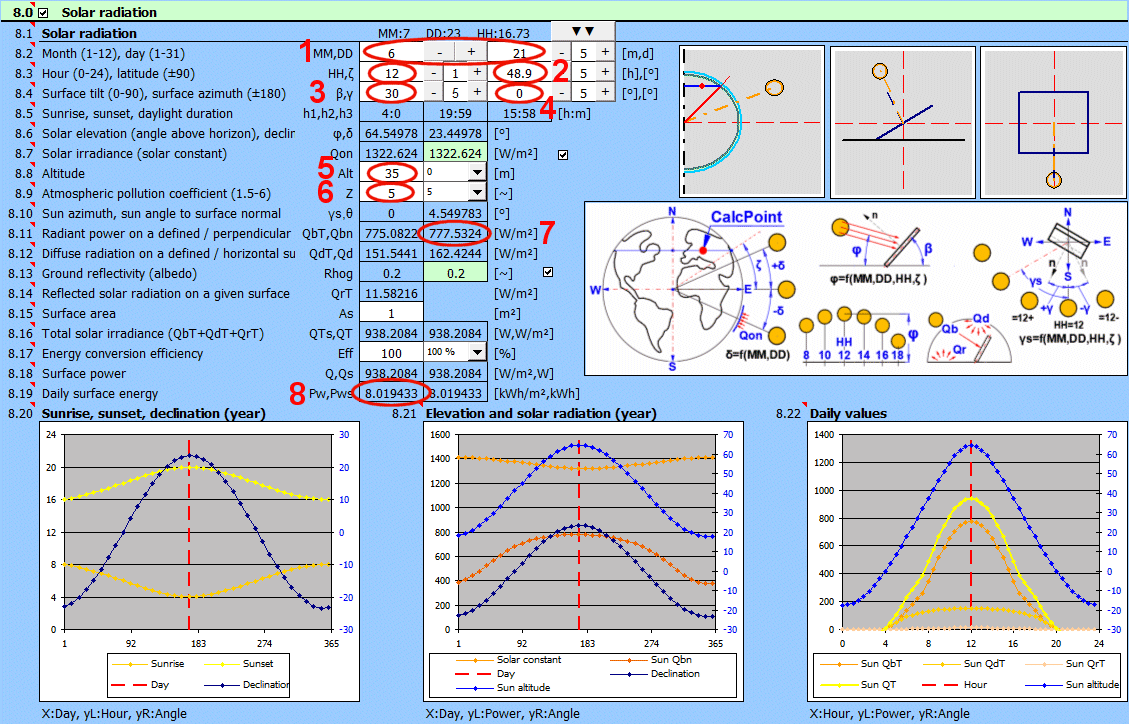
In einem Servicegebäude mit Flachdach (Grundriss 5 x 14 m).
Wandflächen: Im Bild definiert.
Wärmeübergangskoeffizienten: In der Tabelle definiert.
Äußere Bedingungen: T4=-10 °C, Wind 10 m/s.
Gewünschte Temperaturen und Bedingungen: T1=12 °C, T2=22 °C, T3=15 °C.
Eingangsbedingungen: Wärmequellen QH1=1000 W, QH2=2000 W, QH3=1500 W.
Beide Aufgaben können mit demselben mathematischen Modell gelöst werden.
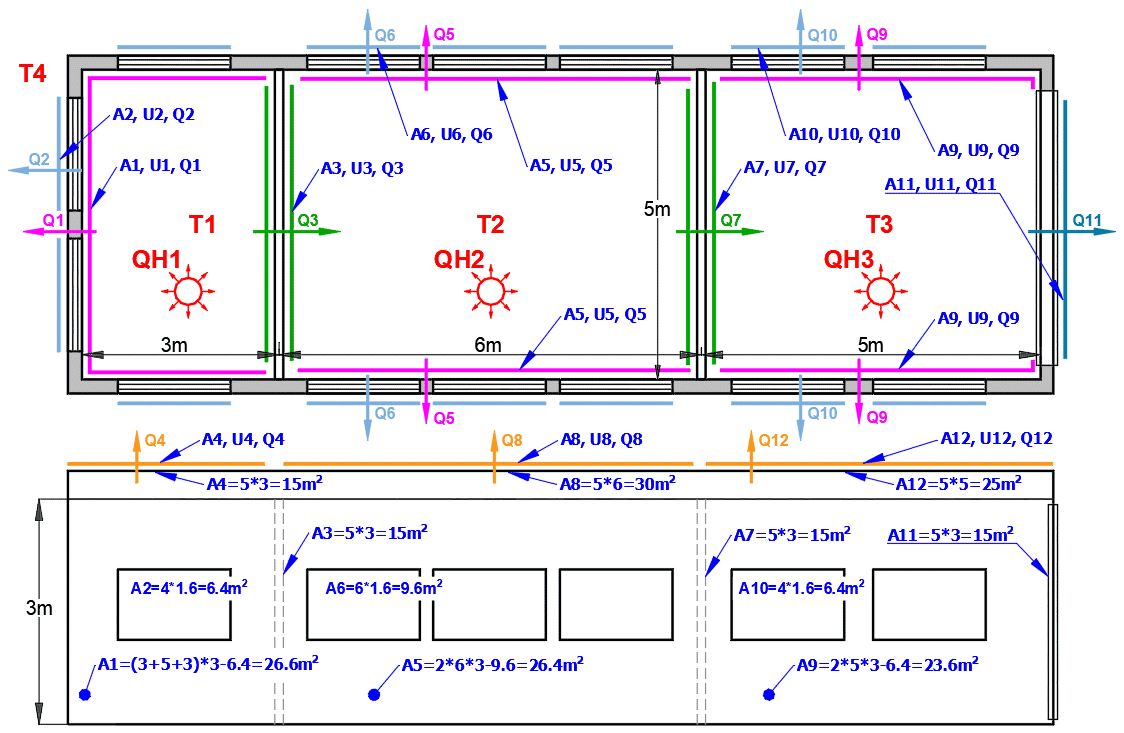
In Abschnitt [4.0] sind die Wärmeübergangskoeffizienten U für die einzelnen
Wände gelöst und in der Liste der gelösten Wände gespeichert.
1. Stellen Sie ein, welche Werte aus den gelösten Wänden in die Tabelle
übertragen werden sollen.
2. Laden Sie schrittweise die Wändeinformationen für die einzelnen Räume.
Natürlich ist es möglich, die U-Werte direkt einzugeben, z.B. aus dem
Lieferantenkatalog.
3. Stellen Sie die tatsächliche Fläche für jede Wand gemäß Abbildung ein
(A1=26,6, A2=6,4,.....).
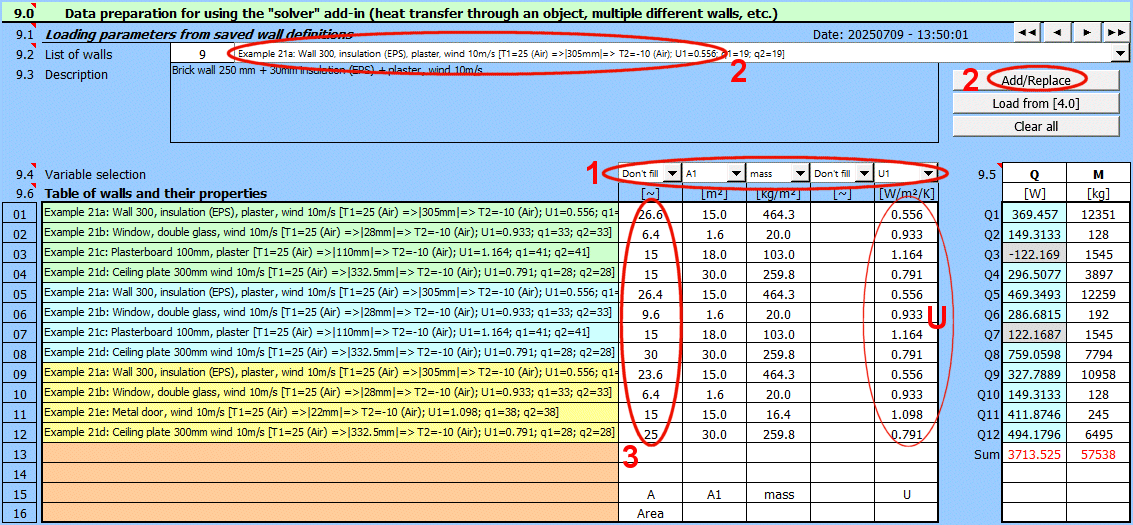
4. Definieren Sie in der Spalte Q den Wärmestrom für jede Wand nach der Formel Q
= dT * A * U (dT ... Temperaturdifferenz, A ... Wandfläche, U ...
Wärmeübergangskoeffizient).
Q1 = (T1 - T4) * A1 * U1
Q2 = (T1 - T4) * A2 * U2
Q3 = (T1 - T2) * A3 * U3
Q4 = (T1 - T4) * A4 * U4
............
5. Definieren Sie Bedingungen, die besagen, dass der Wärmestrom aus jedem Raum
der Leistung der Wärmequelle entsprechen muss.
Q1+Q2+Q3+Q4-QH1=0
Q5+Q6+Q7+Q8-Q3-QH2=0
Q9+Q10+Q11+Q12-Q7-QH3=0
6. Stellen Sie geeignete Anfangswerte für die Wärmequellen ein (z.B. QH1=500,
QH2=1500, QH3=1500).
7. Stellen Sie die gewünschten Temperaturen gemäß Aufgabenstellung ein.
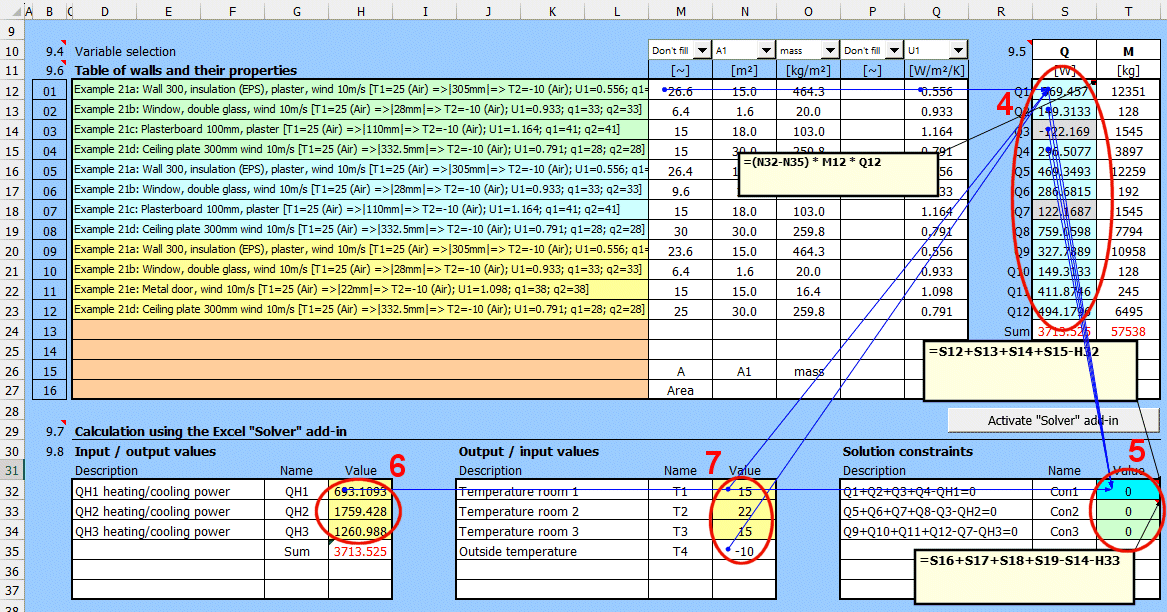
1. Starten Sie das Add-In "Solver" (Excel-Menü "Daten").
2. Geben Sie die Zelle und den Wert ein, der erreicht werden soll: "Ziel
setzen:".
3. Geben Sie die Zellen ein, die geändert werden sollen: "Durch Ändern der
Variablenzellen:".
4. Fügen Sie weitere Bedingungen hinzu, die erfüllt werden müssen: "Unter
Beachtung der Nebenbedingungen:".
5. Starten Sie die Lösung der Aufgabe: "Lösen".
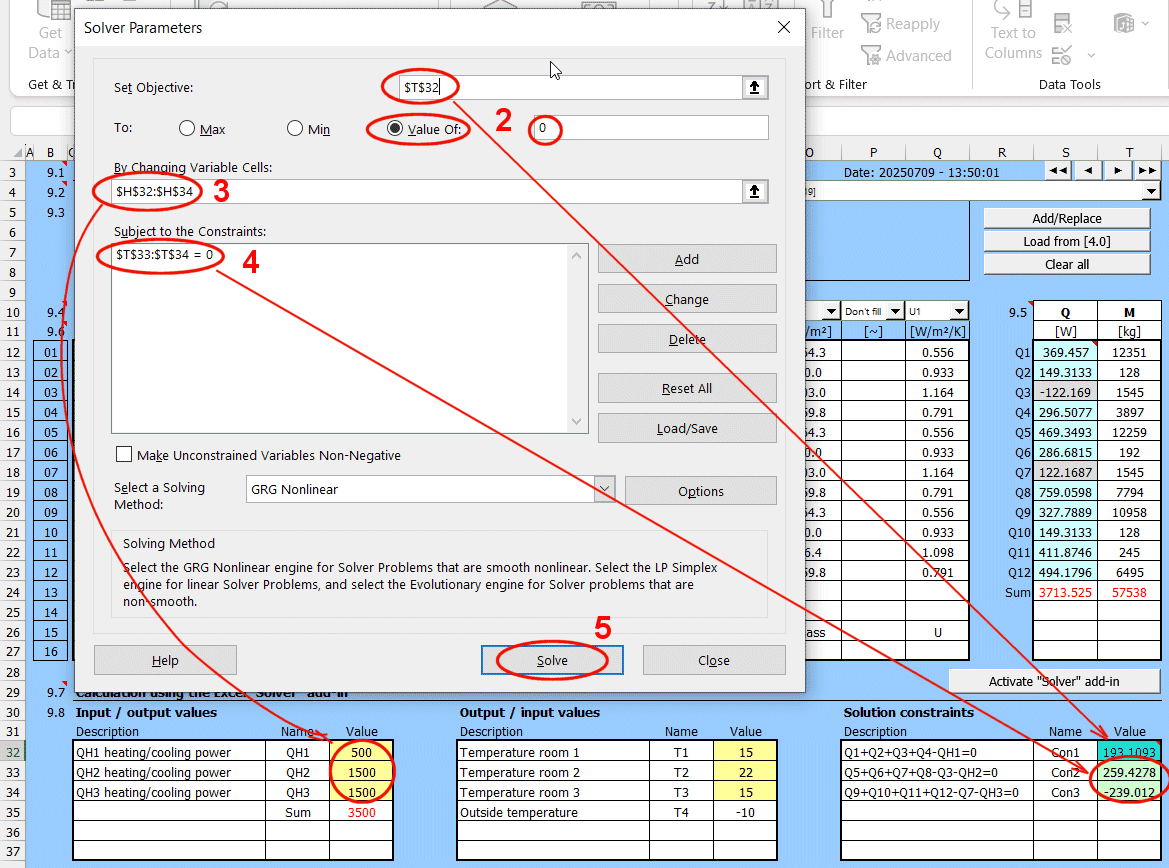
Nach Abschluss der Lösung sollten sich die gewünschten Werte (3) und (4) ändern,
und ein Dialogfeld wird angezeigt.
1. Wählen Sie, ob die Lösung beibehalten werden soll.
2. Bestätigen Sie: "OK".
3,4. Lösungsergebnisse.
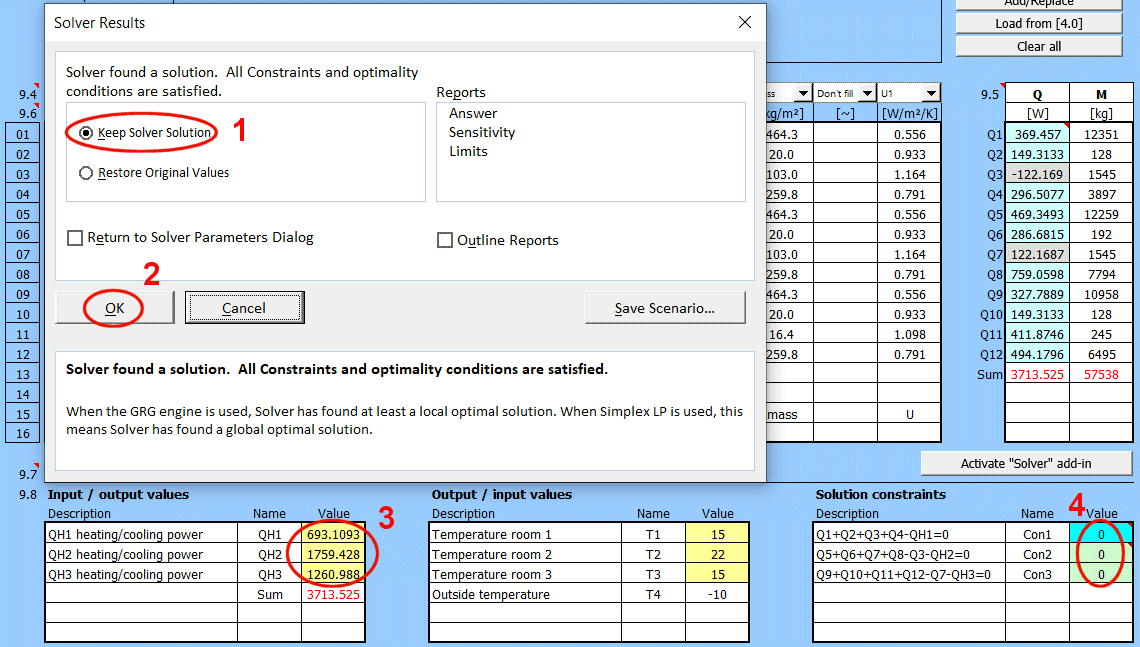
Auf die gleiche Weise wird Aufgabe B gelöst, bei der für die gegebenen Heizleistungen (3) die Raumtemperaturen T1, T2, T3 geändert werden.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
Literaturliste:
EN
[01] YUNUS A. ÇENGEL, AFSHIN J. GHAJAR: Heat and Mass Transfer: Fundamentals
& Applications, 5th Edition, McGraw-Hill Education.
[02] YUNUS A. ÇENGEL: Heat Transfer a Practical Approach, Second Edition.
[03] MORAN, M.J., SHAPIO, H.N.: Fundamentals of engineering thermodynamics. 8th
Edition New York: John Wiley a sons, 1990.
[04] DEWITT, BERGMAN, LAVINE: Fundamentals of Heat and Mass Transfer 6th Edition
[05] WARREN M.ROHSENOW, JAMES R.HARTNETT, YOUNG I.CHO: Handbook of Heat
Transfer, 3th Edition, McGraw-Hill
[06] SCHLUNDER, BELL, HEWITT, SPALDING: Heat Exchanger
Design Handbook, VDI-Verlag GmbH, 1983.
[07] LOIS THEODORE: Heat Transfer Applications for the
Practicing Engineer, John Wiley & Sons, Inc., 2011.
[08] MYER KUTZ: Heat-Transfer Calculations,
McGraw-Hill
[09] HOLMAN, J.P.: Heat Transfer, 10th. Edition, New
York: McGraw-Hill
[10] HOLMAN, J.P. Thermodynamics. 4th. New York:
McGraw-Hill Book Company, 1988. 780 s. ISBN 0-07-029633-2.
[11] MOHAMED M. EL-AWAD: Optimisation Analyses of
Fluid- Thermal Systems Using Excel,
[12] FRANK KREITH, RAJ MANGLIK, MARK BOHN: Principles
of Heat Transfer, Cengage Learning, Inc., 2011
CZ
[13] HORÁK VLADIMÍR, STŘEDA IVO: Mechanika tekutin
- Termomechanika, Strojírenská příručka, Scientia sro.
[14] RANEVI,K. Termodynamické tabulky. 1.vyd.
Bratislava: ALFA 1984. 313s. [L5] HAEK, P. Tabulky pro tepelnou techniku. 1
.vyd. VB Ostrava, 1980, 247 s.
[15] SAZIMA,M., KMON1OEK,V., SCHNELER,J. Teplo. 1.vyd.
Praha: SNTL, 1989. 588 s. Technický průvodce. ISBN 80-03-00043-2.
[16] M.A.MICHEJEV: Základy sdílení tepla, Průmyslové
vydavatelství, 1952
[17] PETRAK,J., DVOAK, Z., KLAZAR, L., SYNEK, V.
Chiadivo R134a, (1.vyd.) VUT, 1993. 72s.
[18] MIROSLAV JÍLEK, ZDENĚK RANDA: Termomechanika -
sbírka příkladů, ČVUT, 2004
Standards:
ASTM C1340-2015 ... Estimation of Heat Gain or Loss Through Ceilings Under
Attics Containing Radiant Barriers...
ISO 12241:2022
Tepelněizolační výrobky pro zařízení budov a průmyslové instalace - Pravidla
výpočtu
Thermal insulation for building equipment and industrial installations —
Calculation rules
Isolation thermique des équipements de bátiments et desinstallations
industrielles — Méthodes de calcul
Wärmedammung an haus- und betriebstechnischen Anlagen — Berechnungsregeln
^