Die Berechnung ist bestimmt für den geometrischen- und Festigkeitsentwurf und die Festigkeitskontrolle der gerad- und schrägflkankigen Stirnverzahnungen (äußeren, inneren, Zahnstange). Das Programm löst folgende Aufgaben:
Die Berechnungen verwenden Verfahren, Algorithmen und Angaben aus Normen ANSI, ISO, DIN, BS und aus der Fachliteratur.
Normenverzeichnis: ISO 6336, ISO 1328, DIN 3990,
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Der komplette Text betreffs der Theorie befindet sich im Dokument: Evolventenverzahnung - Theorie
Zahnradgetriebe teilen wir ein in:
Kraftübertragende Getriebe - Bei vor allem für Leistungsübertragung und Leistungstransformation bestimmten Getrieben ist es nötig, den Festigkeitsentwurf/die Festigkeitskontrolle durchzuführen (z. B. Antriebsmaschinen, Industriegetriebe..).
Nicht- kraftübertragende Getriebe - bei Getrieben, bei denen das übertragene Moment mit Hinsicht auf die Radgröße gering ist, ist es nicht nötig, den Festigkeitsentwurf/die Festigkeitskontrolle durchzuführen (z. B. Geräte, Regelungstechnik..).
Die Aufgabe eines Entwurfes der Stirnverzahnung ist nicht direkt lösbar und bietet eine beträchtliche Freiheit in der Wahl der Durchmesser- und Breitenparameter der Zahnräder. Es ist also nötig, iterativ vorzugehen und die Lösung schrittweise zu präzisieren und die überwachten Parameter abzustimmen.
Durch dieses Verfahren erhalten Sie eine schnelle Ansicht der Parameter des entworfenen Getriebes. Auch wenn das so entworfene Getriebe normal gebrauchsfähig ist, können Sie durch eine stufenweise Optimierung einer ganzen Reihe Parameter die Eigenschaften des entworfenen Getriebes wesentlich verbessern. Bei dem Entwurf verfahren Sie wie folgt:
Vor der Parameteroptimierung zuerst den oben beschriebenen "Schnell- (Orientierungs-) Entwurf " durchführen. Dann verfahren Sie, wie folgt:
Bei einem Entwurf der Stirnverzahnung kommt die Aufgabe des Entwurfs der Verzahnung mit einem gegebenen Achsabstand am häufigsten vor. Bei diesem Entwurf verfahren Sie wie folgt:
Bei einem Entwurf des nichtkraftübertragenden Getriebes sind die Festigkeitsparameter nicht zu lösen und zu kontrollieren. Wählen Sie deshalb direkt eine geeignete Anzahl der Zähne und ein geeignetes Modul [4.1, 4.7] und kontrollieren Sie die Maße der entworfenen Verzahnung.
In diesem Absatz die Grundeingangsparameter der entworfenen Verzahnung eingeben.
Die Leistung für das Antriebsrad eingeben. Übliche Werte befinden sich im Bereich 0.1 - 3000 kW / 0.14-4200 HP, in Extremfällen bis zu 65000 kW /100000 HP.
Die Drehzahl für das Antriebsrad eingeben. Die extreme Drehzahl kann auch bei 150 000 U/min liegen. Die Drehzahl des Antriebsrades wird aus der Anzahl der Zähne der beiden Räder berechnet.
Das ist ein Berechnungsergebnis und kann nicht eingegeben werden.
Ein optimales Übersetzungsverhältnis bewegt sich im Bereich 2-8. In Extremfällen kann es einen Wert bis zu 20 erreichen. Das Übersetzungsverhältnis geben Sie im linken Eingangsfeld aus der Tastatur ein. Im rechten Aufrollverzeichnis befinden sich die empfohlenen Werte des Übersetzungsverhältnisses und bei der Auswahl aus dieser Liste wird der ausgewählte Wert in das Feld links automatisch ergänzt.
Da das tatsächliche Übersetzungsverhältnis ein Quotient der Anzahl der Zähne der beiden Räder ist (ganze Zahlen), wird das tatsächliche Übersetzungsverhältnis meistens von dem verlangten (eingegebenen) unterschiedlich sein. Der Wert des "tatsächlichen Übersetzungsverhältnisses" ist links angeführt, rechts steht dann die prozentuale Abweichung vom verlangten Übersetzungsverhältnis. Diese Abweichung sollte für das Übersetzungsverhältnis sein im Bereich:
i = 1 - 4.5 ...........+- 2.5%
,auch größer als 4.5...+- 4.0%
In der Berechnung kann die Tangentialkraft eingegeben werden, was eigentlich eine Kraft ist, mit der die Zahnstange auf das Ritzel wirkt, und die Bewegungsgeschwindigkeit der Zahnstange (Umfangsgeschwindigkeit des Ritzels). Aus diesen beiden Werten werden anschließend die übertragene Leistung und das Ritzeldrehmoment berechnet. Da die Zahnstange für eine Vielzahl von unterschiedlichen Konstruktionslösungen angewendet werden kann, ist diese nachzuberechnen (abzuschätzen) und die Übersetzungsanforderungen auf diese zwei Werte umzurechnen.
Geben Sie die Kraft ein, die auf das Ritzel wirkt (Zahnstangenbelastung).
Geben Sie die Zahnstangengeschwindigkeit ein.
Wird aus der übertragenen Kraft und Geschwindigkeit berechnet.
Pw[kW] = Ft * v / 1000
Wird aus der Umfangsgeschwindigkeit und dem Ritzeldurchmesser berechnet.
Wird aus der Leistung und Drehzahl berechnet.
Bei einem Entwurf eines kräfteübertragenden Getriebes weitere ergänzende Parameter für den Betrieb und die Herstellung in diesem Absatz eingeben . Trachten Sie bei der Wahl und Eingabe dieser Parameter nach der Höchstgenauigkeit, weil jedes von den Parametern einen dramatischen Einfluss auf die Eigenschaften des entworfenen Getriebes haben kann.
Dieses wird vor allem nach folgenden Aspekten gewählt :
In der Regel wird der Grundsatz eingehalten, dass die Härte des Ritzels die des Rades (20-60 HB) überschreiten soll, wobei die Härtedifferenz mit der zunehmenden Radhärte und dem zunehmenden Übersetzungsverhältnis zunimmt. Einer schnellen Orientierung wegen führen wir die Werkstoffeinteilung in 8 mit Buchstaben A-H gekennzeichneten Gruppen durch. Die Werkstoffauswahl aus einem Aufrollverzeichnis durchführen, getrennt für das Ritzel und für das Rad. Wenn Sie ausführlichere Informationen über den gewählten Werkstoff benötigen, in die Tabelle "Werkstoff" wechseln.
Werkstoffe A,B,C,D s. g.. Weichräder - Die Verzahnung wird erst nach der Wärmebehandlung hergestellt, sie zeichnen sich durch eine gute Einlaufsfähigkeit aus, sie stellen keine besonderen Anforderungen an Genauigkeit und Auflagerungsfestigkeit, wenn wenigstens ein Rad im Getriebe aus dem gewählten Werkstoff besteht.
Werkstoffe E,F,G,H s. g.. Harträder - Höhere Herstellungsaufwände (Härten +100%, Zementieren +200%, Nitrieren +150%). Die Wärmebehandlung wird nach der Verzahnungsherstellung durchgeführt. kompliziertes Erreichen der benötigten Genauigkeit. Oft sind aufwändige Schlicht-Arbeitsgänge nach der Wärmebehandlung notwendig (Schleifen, Läppen).
Eigene Werkstoffwerte - Wenn Sie von einem für die Verzahnungsherstellung in der gelieferten Werkstofftafel nicht enthaltenen Werkstoff Gebrauch machen möchten, ist es nötig, über den eigenen Werkstoff eine Reihe von Angaben einzugeben. In die Tabelle "Werkstoffe" wechseln. Die ersten 5 Zeilen in der Werkstofftafel sind für die Definition der eigenen Werkstoffe vorbehalten. In der für die Benennung des Werkstoffes bestimmten Spalte den Werkstoffnamen eingeben (er wird in der Auswahlliste angezeigt), und schrittweise füllen Sie sämtliche Parameter (weiße Felder) aus. Nach der Ausfüllung wechseln Sie zurück in die Tabelle "Berechnung", wählen den neu definierten Werkstoff aus und setzen die Berechnung fort.
Die Einstellung dieser Parameter beeinflusst wesentlich die Berechnung der Sicherheitsfaktoren. Deshalb suchen Sie nach der besten Spezifikation bei der Auswahl der Belastungstypen. Beispiele der Antriebsmaschinen:
Die Einstellung dieser Parameter beeinflusst wesentlich die Berechnung der Sicherheitsfaktoren. Deshalb suchen Sie bei der Auswahl der Belastungstypen nach der besten Spezifikation. Beispiele der Antriebsmaschinen:
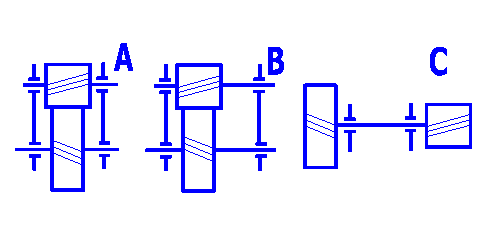
Die Einstellung von diesem Parameter beeinflusst die Berechnung des Sicherheitsfaktors. Die Sitzart ist durch den Koeffizienten der Ungleichmäßigkeit der Belastung definiert, hervorgerufen vor allem durch die Wellendurchbiegungen. Die Sitzart nach der folgenden Definition und Abbildung wählen.
Typ1: Ein steifes Gehäuse, steife Wellen, robuste Rollen- oder Kegelrollenlager.
Typ2:Ein weniger steifes Gehäuse, längere Wellen, Kugellager.
Bei der Wahl der Genauigkeitsstufe des entworfenen Getriebes ist es nötig, auf betriebliche Bedingungen, Funktionalität und Herstellungsmöglichkeit Rücksicht zu nehmen. Bei dem Entwurf beginnen wir bei:
Die Verzahnungsgenauigkeit wird nur so hoch, wie unerläßlich gewählt, weil das Erreichen einer hohen Genauigkeitsstufe aufwändig, schwer und mit höheren Ansprüchen auf die technologische Ausrüstung bedingt ist.
| Genauigkeitsstufe ISO 1328, ANSI/AGMA 2015 |
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Genauigkeitsstufe AGMA |
13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 |
| Höchstwert der Oberflächenrauheit Ra max [nm] | 0.1-0.2 | 0.4 | 0.8 | 1.6 | 1.6 | 3.2 | 6.3 | 12.5 | 25 |
| Höchstumfangsgeschwindigkeit [m/s] geradflankige Verzahnung | 80 | 60 | 35 | 15 | 8 | 5 | 3 | 3 | 3 |
| Höchstumfangsgeschwindigkeit [m/s] schrägflanike Verzahnung | 100 | 80 | 50 | 30 | 12 | 8 | 5 | 3 | 3 |
|
Anwendungsbereich |
Genauigkeitsstufe. ISO 1328, ANSI/AGMA 2015 |
Genauigkeitsstufe. AGMA 2000-A88 |
| Kontrollräder | 2 - 4 | 13-12 |
| Messgeräte | 3 - 6 | 13-10 |
| Turbinenreduktionsgetriebe | 3 - 5 | 13-11 |
| Flugzeugreduktionsgetriebe | 3 - 6 | 13-10 |
| Werkzeugmaschinen | 3 - 7 | 13-9 |
| Flugzeugmotoren | 5 - 6 | 11-10 |
| Schnelllaufende Getriebe | 5 - 6 | 11-10 |
| Personenkraftwagen | 6 - 7 | 10-9 |
| Industriegetriebe | 7 - 8 | 9-8 |
| Leichtmotoren für Schiffe | 7 | 9 |
| Walzwerke, Lokomotiven | 8 - 9 | 8-7 |
| Schwermotoren für Schiffe, Traktoren | 8 - 9 | 8-7 |
| Baustellen-, Landwirtschaftsmaschinen | 8 - 10 | 8-6 |
| Textilmaschinen | 7 - 9 | 9-7 |
Der Koeffizient gibt das Verhältnis zwischen dem maximalen (Anlaufsdrehmoment) und Nenndrehmoment der Antriebsmaschine an. Der Koeffizient beeinflusst wesentlich die Sicherheitsberechnung bei einmaliger Überlastung (Anlauf) des Getriebes. Der Koeffizient ist im Katalog des Antriebsherstellers zu finden.
Drehstromasynchronmotor ... 2-3
Der Parameter bestimmt die verlangte Standzeit in Stunden. Orientierungswerte in Stunden sind in der Tafel angeführt.
|
Anwendungsbereich |
Dauerhaltbarkeit |
| Haushaltsmaschinen, nur selten benutzte Anlagen | 2000 |
| Elektrische Handwerkzeuge, Maschinen für kurzzeitigen Betrieb | 5000 |
| 8-Stundenbetrieb | 20000 |
| 16-Stunden-Betrieb | 40000 |
| Maschinen für durchgehenden Betrieb | 80000 |
| Maschinen für durchgehenden Betrieb mit langer Lebensdauer | 150000 |
Geben Sie die Anzahl der Zyklen für die Zahnbelastung für das Ritzel und für die Zahnstange ein.
Empfohlene Werte des Sicherheitskoeffizienten bewegen sich im Bereich:
Entschließen Sie sich, ob Sie eine geradflanike- oder schrägflankige Verzahnung entwerfen wollen. Für die Wahl können Sie folgende Empfehlung verwenden:
Bei dem "Automatischen Entwurf" werden die Getriebeparameter auf Grund der eingegebenen betrieblichen und Leistungsparameter [1.0; 2.0] und auf Grund der allgemein gültigen Empfehlungen eingestellt. Durch manuelle Optimierung können Sie meistens eine Verzahnung mit besseren Parametern (Gesamtgewicht, Größe) entwerfen, eventuell die Maße nach Ihren konstruktiven Ansprüchen anpassen.
In diesem Absatz bestimmen Sie die Parameter des Bearbeitwerkzeuges und das Kopfspiel in der Verzahnung. Diese Parameter beeinflussen die meisten Maße der Verzahnung, die Zahnform und daraus folgende Festigkeitsparameter, Steifigkeit, Standzeit, Geräusch, Wirkungsgrad und andere. Wenn die genauen Parameter des Herstellungswerkzeuges Ihnen nicht bekannt sind, verwenden Sie den genormten Typ aus der Auswahlliste in der Zeile [3.1] und zwar:
1. DIN 867 (a=20deg, ha0=1.25, hf0=1.0, ra0=0.38, d0=0, anp=0deg, ca=0.25)
für die Berechnung in den SI-Einheiten und
3. ANSI B6.1 (a=20deg, ha0=1.25, hf0=1.0, ra0=0.3, d0=0deg, anp=0, ca=0.35) für
die Berechnung in den Zoll-Einheiten.
In dem Formular können Sie zwei Werkzeugtypen definieren und zwar mit einer Protuberanze (A) und ohne eine Protuberanze (B). Wenn Sie ein Werkzeug ohne eine Protuberanze definieren, geben Sie das Maß der Protuberanze d0=0 ein. Die Werkzeugmaße nach den Maßen in der Abbildung als das Modulvielfache eingeben "Wert"x"Modul" (Berechnung in den SI-Einheiten) oder als den Quotienten "Wert"/"Diametral Pitch" (Zoll-Berechnung). Der Eingriffswinkel ist im Absatz [4] zu wählen. Der Zahnfuß kann entweder abgeschrägt oder abgerundet sein, deshalb nur ein Verfahren auswählen.
Im Diagramm ist die Zahnform des Werkzeuges für Rad/Ritzel aufgezeichnet. Wenn Sie die Werkzeugmaße ändern, ist die entsprechende Taste zu betätigen, die die Wiederaufzeichnung nach aktuellen eingegebenen Werten sicherstellt.
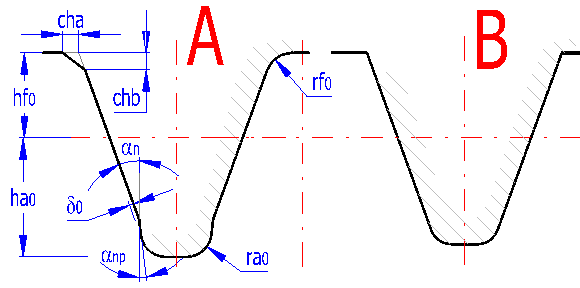
Die genaue Zahn-, Zahnradform, Kontrolle der Interferenzen usw. sind im Absatz über die grafische Ausgabe und CAD-Systeme beschrieben.
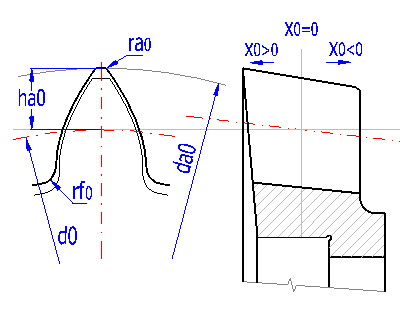
Die innere Verzahnung ist in einer überwiegenden Mehrheit von Fällen mit Hilfe eines scheibenförmigen Werkzeuges hergestellt. Für Zwecke dieser Berechnung betrachten wir ein Werkzeug, das die grundlegenden Parameter mit der entworfenen Verzahnung übereinstimmend hat(an0=an, b0=b, mn0=mn). Der Winkel b kann jedoch bei der Herstellung der inneren Verzahnung nicht beliebig gewählt werden, es ist nötig von den Eigenschaften der Werkzeugmaschine und den erreichbaren Werkzeugen auszugehen und bei dieser Wahl den Technologen heranzuziehen.
Ein Beispiel so eines Werkzeuges ist in der Abbildung. Der aktuelle Anschliff des Werkzeuges entspricht seiner Einheitskorrektur x0. Beim Werkzeugnachschliff kommt es zur Änderung der Korrektur und dadurch auch zur Änderung des Kopfdurchmessers des Werkzeuges. Wenn die Höhenkorrekturgröße x0 nicht bekannt ist, genügt es, den aktuellen Kopfdurchmesser zu messen und durch eine Änderung der Höhenkorrektur x0 [3.13] den Kopfdurchmesser da0 [3.14] auf den gewünschten Wert abzustimmen.
Im Hinblick auf die Herstellungsart und Geometrie der Zahnstange ist das Werkzeug in diesem Fall ein direktes Negativ der hergestellten Verzahnung (Geradverzahnung). Bei einer Schrägverzahnung ist das Werkzeug ein direktes Negativ der hergestellten Verzahnung im normalen Schnitt.
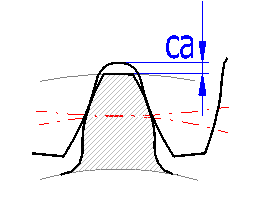
Das Einheitskopfspiel "ca" beeinflusst den Kopfkreisdurchmesser. Üblich wird ca=0.25 gewählt, was bei den üblich verwendeten Höhenkorrekturen die Interferenzverhinderung gewährleistet. Wenn die Werkzeugparameter genau bekannt sind, ist es möglich c* kleiner zu wählen und zwar 0.15 bis 0.1 und damit eine Erhöhung des Profileingriffskoeffizienten zu erreichen. Die Interferenz ist möglich und ratsam auf einer Detailzeichnung zu kontrollieren, siehe Absatz über grafische Ausgabe und CAD-Systeme. In der Zeile [3.10] ist das minimale Kopfspiel angeführt, das mit dem erwählten Werkzeug zu erreichen ist. Die Wahl eines kleineren Kopfspiels wird durch rote Verfärbung des Eingabefeldes signalisiert. Die Taste "<" überträgt den Minimalwert ins Eingabefeld. Das minimale Einheitskopfspiel kann durch eine Vergrößerung der Fußhöhe des Werkzeuges verringert werden.
In diesem Absatz entwerfen Sie die Geometrie des Zahngetriebes. Der Entwurf der Geometrie beeinflusst wesentlich eine Reihe von weiteren Parametern wie Funktionalität, Sicherheit, Haltbarkeit, Preis.
Die Anzahl der Zähne des Ritzels eingeben. Die Anzahl der Zähne des Rades ist auf Grund des verlangten Übersetzungsverhältnisses nachträglich zu berechnen. Das Auffinden der optimalen Anzahl der Zähne ist eine weder eindeutige noch direkt lösbare Aufgabe. Die Anzahl der Zähne beeinflussen die Eingriffsverhältnisse, Geräuschpegel, Getriebeeffizienz, Herstellungskosten. Deshalb wird am meisten die Anzahl der Zähne gewählt und nach den qualitativen und Festigkeitskennzahlen präzisiert.
Allgemein gilt die Regel, dass die Erhöhung der Anzahl der Zähne (bei einem konstanten Achsabstand) führt zur:
A) Für beide Räder normalgeglüht/vergütet - Weichräder
B) Für gehärtetes Ritzel und nicht gehärtetes Rad (oder beide Räder nitriert)
C) Die beiden Räder oberflächengehärtet (einsatzgehärtet)
Es gilt, dass eine größere Anzahl von Zähnen für eine größere Leistungen und ein kleineres Übersetzungsverhältnis gewählt werden.
Der rot hervorgehobene Text zeigt die teilbare Anzahl der Zähne an, welche vermieden werden sollten.
Dieser bestimmt die Parameter des Grundprofils und ist auf einen Wert von 20 Grad genormt. Durch eine Änderung des Eingriffswinkels a/F ist es möglich, funktionelle und Festigkeitseigenschaften zu beeinflussen. Die Änderung des Eingriffswinkels benötigt allerdings nicht genormte Herstellungswerkzeuge. Wenn es also keine besondere Begründung für die Anwendung eines anderen Eingriffswinkels gibt, verwenden Sie den Wert von 20 Grad.
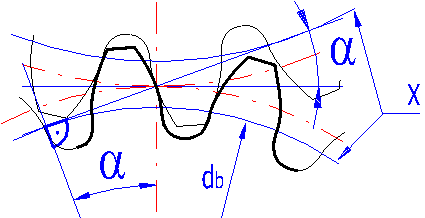
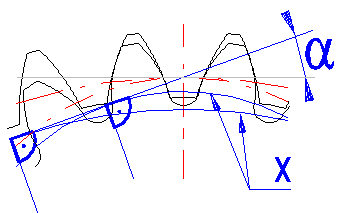
Mit dem Buchstaben "X" ist der Grundkreis gekennzeichnet.
Durch eine Vergrößerung des Eingriffswinkels ist es möglich:
Wahl der Werte
Wenn Sie keine speziellen Anforderungen für die entworfene Verzahnung haben, empfehlen wir den Winkel von 20 Grad zu verwenden.
Die Verzahnung mit dem Schrägungswinkel = 0 (geradflankige Verzahnung) wird bei langsam laufenden und stark beanspruchten Getrieben verwendet. Bei schnell laufenden Getrieben dort, wo Schwierigkeiten mit dem Auffangen von axialen Kräften bestehen würden und wo es kein Problem mit dem erhöhten Geräuschpegel gibt.
Die Verzahnung mit dem Schrägungswinkel > 0 (Schrägverzahnung) wird bei schnelllaufenden Getrieben verwendet und weist einen niederen Geräuschpegel und eine bessere Tragfähigkeit aus und erlaubt eine kleinere Anzahl der Zähne ohne Unterschneidung.
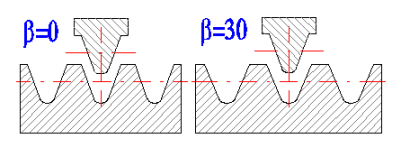
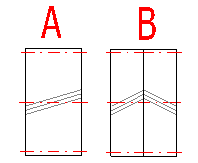
Der Winkel Beta wird aus der folgenden Reihenfolge gewählt - 6,8,10,12,15,20 Grad (Abb. A). Wenn es sich um eine doppelte Verzahnung oder eine Pfeilverzahnung (Abb. B) handelt, ist es möglich, auch die Werte 25,30,35,40 Grad zu verwenden.
Durch den Läufer den Wert des dimensionslosen Koeffizienten einstellen, der das Verhältnis der Ritzelbreite und des Ritzeldurchmessers ausdrückt [4.5].
Dieser Parameter dient für den Entwurf der Modulgröße und damit auch der grundlegenden geometrischen Radparameter (Breite, Durchmesser). Der empfohlene Maximalwert ist in der rechten Spalte angeführt und von dem gewählten Radwerkstoff, der Radsitzart und dem Übersetzungsverhältnis des Getriebes abhängig. Die Einstellung dieses Parameters durch Ziehen des in der Zeile [4.4] angebrachten Läufers. Nach der Einstellung dieses Parameters die Schaltfläche "Verzahnung entwerfen" drücken. Durch dieses Verfahren entwerfen Sie eine Verzahnung, die der verlangten Sicherheit [2.9] und den anderen Eingangsparametern entspricht.
Nach dem Verlauf des "Verzahnungsentwurfes " Maße (Radbreiten und Raddurchmesser, Gesamtgewicht) kontrollieren. Wenn Sie mit dem Resultat nicht zufrieden sind, passen Sie den Parameter des Verhältnisses der Ritzelbreite und des Ritzeldurchmessers [4.4, 4.5] an und wiederholen Sie den "Verzahnungsentwurf".
Kleinere Werte - Entwurf eines engeren Rades, ein größeres Modul, Geradflankige Verzahnung
größere Werte - Entwurf eines breiteren Rades , ein
kleineres Modul, Schrägverzahnung
Es ist der wichtigste Parameter, der die Zahngröße und dadurch auch die Größe des ganzen Getriebes bestimmt. Es gilt allgemein, dass es für eine größere Anzahl der Zähne ein kleineres Modul benutzt werden kann (der größere P-Wert in der Zoll-Version der Berechnung) und umgekehrt. In dem rechten Entfaltungsmenü befinden sich die genormten Modulwerte / (Diametral Pitch in der Zoll-Version der Berechnung) und bei der Auswahl aus dieser Auflistung ergänzt sich der ausgewählte Wert im Feld links automatisch.
Der Entwurf der richtigen Modulgröße ist eine relativ komplizierte Aufgabe. Wir empfehlen deshalb, das Verfahren auf Grund des Verhältnisses der Ritzelbreite zu dessen Durchmesser zu verwenden [4.5].
Die Verzahnungsbreite b der einzelnen Räder ist gemessen am Teilzylinder . Die Breite der Ritzelverzahnung wird meistens größer gemacht und zwar um die Größe eines Moduls.
Diese sind von dem gewählten Werkstoff und Bautyp des Getriebes [2.1,2.2,2.5] abhängig. Der empfohlene Wertbereich ist in der vorgehenden Zeile angeführt.
Es ist die gemeinsame Breite der beiden Räder auf den Wälzzylindern. Wenn die Räder nicht versetzt sind (Abb. 4.1), ist das meistens die Radbreite. Diese Breite wird für die Festigkeitskontrollen der Verzahnung verwendet.
Wenn das Anhakfeld in dieser Zeile angehakt ist, ist die "Arbeitszahnbreite" automatisch mit dem kleineren Wert der Zahnbreite aus der vorhergehenden Zeile [4.9] ausgefüllt.
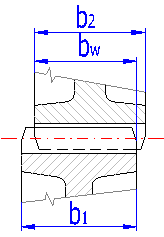
Das Parameter drückt ein Verhältnis zwischen der eingegebenen Ritzelbreite und dessen berechnetem Teilungsdurchmesser aus. Der Maximalwert ist im grünen Feld rechts angeführt.
Dieses ist als Gesamtgewicht der Vollzylinder (ohne Entlastungen und Bohrungen) berechnet. Es dient einer schneller Orientierung beim Entwurf. In Absatz [8.0], ist es möglich, die Berechnung der Gewichts verfeinern.
In der Zeile ist immer der kleinere Wert der Koeffizienten für Ritzel und Rad angeführt. In der ersten Spalte befindet sich der Sicherheitsfaktor für die Berührungsermüdung, in der zweiten Spalte dann
Dieses ist der (kleinste) Lotabstand zwischen den nicht arbeitenden Flanken. Das Flankenspiel ist für die Bildung einer zusammenhängenden Schicht von Schmierstoff auf den Flanken und für die Überbrückung von Herstellungsungenauigkeiten, Verformungen und Wärmeausdehnungen der einzelnen Glieder des Mechanismus nötig. Ein sehr kleines Spiel wird bei Getrieben der Meßsysteme und Geräte verlangt, und wenn dieses nicht ausgeschlossen werden kann, werden Getriebe mit einer automatischen Einstellung des Flankenspiels verwendet. Ein großer Wert des Flankenspiels ist zu wählen bei stark beanspruchten (Wärmeausdehnung) und schnelllaufenden Getrieben (hydraulische Widerstände und Stöße bei Ölverdrängung aus den Zwischenzahnräumen).
In der Praxis wird empirisch gewählt, und es ist möglich, sich nach den empfohlenen Werten in der Zeile [4.16] zu richten.
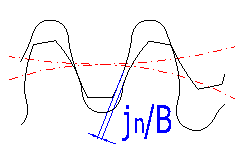
Nach der Eingabe des Flankenspiels ist der Arbeitsachsabstand [6.10] auf die entsprechende Weise angepasst, so dass das eingegebene Flankenspiel entsteht. Bei der Berechnung der Verzahnung für einen genauen Achsabstand [14] ist im Gegenteil die Verzahnungskorrektur [5.6] berichtigt, damit das eingegebene Flankenspiel erreicht ist.
Die Wahl der Verschiebungsfaktoren x1 und x2 ist eine Grundaufgabe bei dem Entwurf der Zahnradgetriebe, vor allem bei Rädern mit geradflankiger Verzahnung. Die Verschiebung beeinflusst nicht nur geometrische, sondern auch Bewegungs- und Festigkeitscharakteristiken. Bei einem Korrekturentwurf sind zuerst die funktionellen Anforderungen zu erfüllen, und dann ist es möglich, die Verschiebungen, Korrekturen so zu optimieren, dass irgendwelche weitere Getriebeparameter verbessert werden.
Durch Annähern oder Entfernen des Werkzeuges in Hinsicht auf die Radmitte ändert sich die Form und dadurch auch die Eigenschaften einer Evolventenverzahnung. So wird eine korrigierte Verzahnung, Verschiebungs-Verzahnung gebildet. In der Abbildung ist:
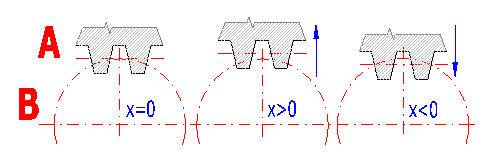
Durch eine Verzahnungskorrektur ist es möglich:
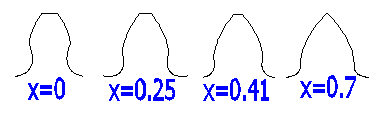
Beispiel eines Zahnprofils (z=10, a=20;
Bei einer Festlegung der Korrekturwerte sind die funktionellen Anforderungen auf die Verzahnung zuerst zu erfüllen, welche zu den Wichtigsten gehören
Zur Sicherung der funktionellen Anforderungen ist es dann möglich, weiter die Höhenkorrekturen zwecks der Verbesserung eines oder mehreren wichtigen Verzahnungsparameter zu optimieren. Von den oft verwendeten Optimierungsmethoden ist es möglich, hier die Verzahnung auf den Ausgleich der Schlüpfe [5.10, 5.11] und auf Minimierung der Schlüpfe [5.12] zu optimieren. Für weitere Optimierungsprozesse gibt es in der Literatur eine Reihe von Empfehlungen und vor allem so genannte Diagramme (Tabellen) der Grenzkorrekturen, die einen anschaulichen Hinblick auf die Möglichkeiten und Wahlen der Korrekturen bieten.
Ein Beispiel der Tafel der Maximalwerte der Korrekturen für einen Faktor

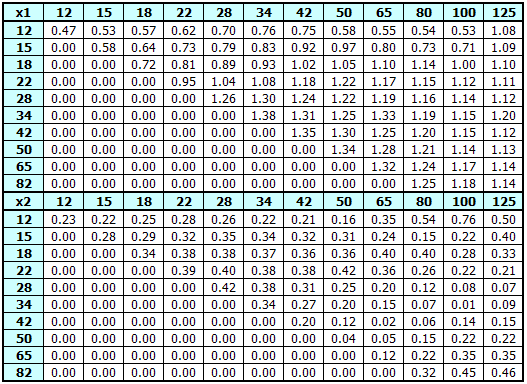
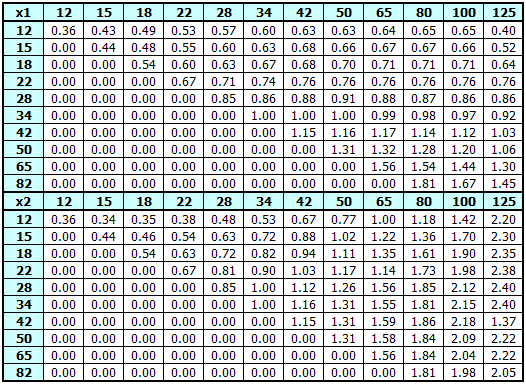
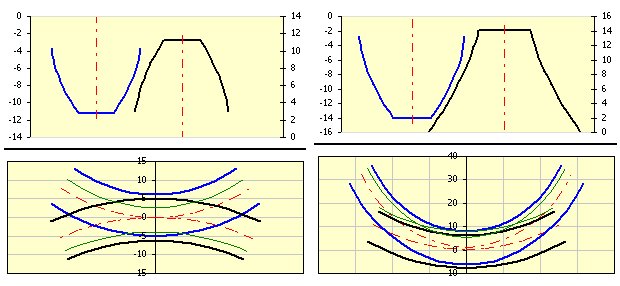
In der linken Abbildung sind alle wichtigen Kreise des wechselseitig eingreifenden Ritzels und Rades angeführt, wo:
In der rechten Abbildung ist die Zahnform des Ritzels (blau) und die Zahnform des Rades (schwarz) angeführt.
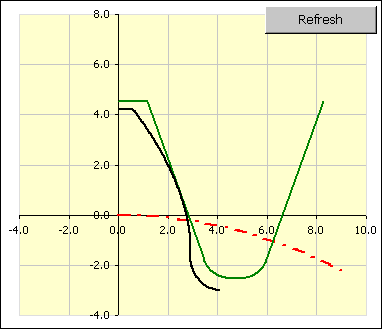
In der Abbildung der Form des Zahnes und des Werkzeuges ist es möglich, visuell die Zahnform und den Werkzeugseingriff zu kontrollieren. Schwarz ist die genaue Zahnform aufgezeichnet, grün dann die genaue Form des Bearbeitungswerkzeuges. Die Umschaltung zwischen der Darstellung des Ritzel- und Radzahnes und Einstellung der Andrehung des Werkzeuges im Eingriff sind in der Zeile [5.15] möglich.
Es ist der Minimalwert einer Korrektur, der verwendet werden kann, ohne dass eine zulässige (kleine, tolerierte) Zahnunterschneidung eintreten würde.
Es ist ein Minimalwert der Korrektur , der verwendet werden kann, ohne dass eine Zahnunterschneidung eintreten würde.
Es ist ein Minimalwert der Korrektur, der verwendet werden kann, ohne dass eine Zahnverjüngung eintreten würde.
Für eine schnelle Verteilungsänderung der Korrekturen ist dieser Läufer bestimmt. Wenn das Anhakfeld rechts vom Läufer angehakt ist, steuert die Läuferbewegung die Verteilung der Korrektursumme [5.6] auf einzelne Räder. Es ist zweckdienlich, diese Funktion im Zeitpunkt zu benutzen, wenn Sie einige der qualitativen oder Festigkeitsparameter der Verzahnung optimieren möchten, von denen die wichtigsten in den Zeilen [5.8-5.14] angeführt sind.
Hier ist die Verteilung des Gesamtverschubes auf das Ritzel und das Rad angeführt. Wenn Sie den Profilverschiebungsfaktor des Ritzels von der Tastatur eingeben wollen, das Anhakfeld in der Zeile [5.5] abhaken (deaktivieren).
In der Spalte links befindet sich das Eingangsfeld für die Eingabe der Summe der Verschiebungsfaktoren, die dann auf einzelne Räder verteilt ist. In der Spalte rechts ist folgend aus der Bedingung des Grenzwalzeingriffswinkels der Minimalwert angeführt. (Die Summe der Verschiebungsfaktoren muss immer größer sein).
Bei einer Korrekturänderung ist es ratsam, das Verhalten dieser Kennzahlen zu überwachen. Eine Überschreitung der kritischen Werte ist durch Farbänderung der Ziffer angezeigt.
Detaillierte Erläuterung [8.1] und [8.2]
Es ist ein dimensionsloser Parameter (Quotient der Zahndicke und des Moduls) und ist vor allem von der Zahnform abhängig. Es wirken hier folgende Parameter:
Es ist üblich 0.25 - 0.4. größere für kleine Werte des Einheitsverschubsfaktors und gehärtete Räder. Ein kleinerer Wert als der empfohlene ist durch einen roten Text angezeigt, die Überschreitung der Grenze der Zahnspitzheit dann mit dem roten Feld.
Eine der häufigsten Optimierungsaufgaben ist das Auffinden solcher Korrekturen x1 und x2 damit Schlüpfe auf Köpfen/Füßen des Rades und Ritzels ausgeglichen sind. Das Prinzip ist in der Fachliteratur beschrieben. In dieser Berechnung ist die Größe des Schlupfes auf dem Fuß (Kopf) des Ritzels (des Rades) in der Zeile [5.10] und [5.11] angeführt. Durch Verschiebung des Läufers in der Zeile [5.5] und dadurch auch durch die Änderung der Korrekturgröße x1 und x2 finden Sie leicht solche Korrekturwerte, bei denen die Größen der Schlüpfe in den Zeilen [5.10] und [5.11] annähernd übereinstimmend sind.
Diese Optimierungsweise ist geeignet für Räder mit annähernd gleicher Zahnanzahl, die aus dem demselben Werkstoff hergestellt werden. Bei der verschiedenen Anzahl von Zähnen greifen die Ritzelzähne öfter ein als die Radzähne und bei den ausgeglichenen Schlüpfen ist dann der Ritzelfuß zur Pittingbildung mehr anfällig.
Günstiger als die Korrektur zum Ausgleich der Schlüpfe [5.10, 5.11] kann daher die Korrektur zum Erreichen der Minimalsumme der Absolutwerte aller Schlüpfe sein. Von Vorteil ist in diesem Fall auch die Steigerung des Wirkungsgrades des Getriebes (es entstehen kleinere Reibungsverluste).
Ausführlichere Informationen [10].
In dieser Zeile wählen Sie aus, ob ein detailliertes Zahnprofil des Ritzels oder des Rades dargestellt werden soll und mit dem Läufer stellen Sie die Andrehung des Werkzeuges im Eingriff ein.
In diesem Absatz werden übersichtlich alle grundlegenden Maßparameter der Verzahnung aufgelistet. Der Anschaulichkeit halber führen wir eine Abbildung der wichtigsten Maßparameter an. Für eine gründlichere Erläuterung der einzelnen Parameter empfehlen wir, von der Fachliteratur Gebrauch zu machen.
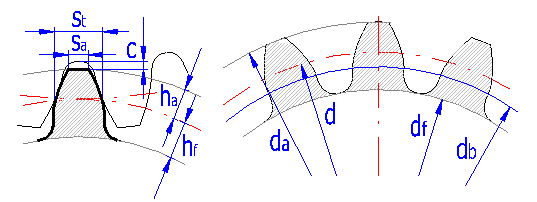
Maßkennzeichnung nach ISO (DIN)
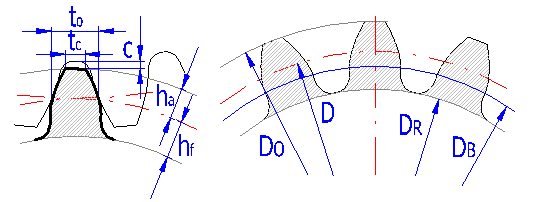
Maßkennzeichnung nach ANSI (AGMA)
Es ist ein dimensionsloser Parameter (Quotient der Zahndicke und des Moduls)
und ist vor allem von der Zahnform abhängig. Es wirken hier folgende Parameter:
- eine größere Zahnanzahl [4.1] = sa* größer
- kleinerer Profilverschiebungsfaktor [5.4] = sa* größer
- kleinerer Eingriffswinkel [4.2] = sa* größer
- eine größere Zahnschrägung [4.3] = sa* größer
- ein größerer Faktor der Zahnkopfhöhe [3.1]= sa* kleiner
Empfohlene Werte
Es ist üblich 0.25 - 0.4. größere für kleine Werte des Einheitsverschubsfaktors
und gehärtete Räder. Ein kleinerer Wert als der empfohlene ist durch einen roten
Text angezeigt, die Überschreitung der Grenze der Zahnspitzheit dann mit dem
roten Feld.
In der Praxis sind manchmal genaue Werte des Kopfkreisdurchmessers zu erreichen. Falls die bereits gegebenen Verzahnungsabmessungen beibehalten werden sollen, kann man den Kopfkreisdurchmesser durch Änderung des Kopfspiels ca* im Absatz [3.11] leicht ändern. Zur Vereinfachung dieser Berechnung dienen die folgenden drei Zeilen. In der zweiten Zeile ist der mögliche Bereich des Kopfkreisdurchmessers angegeben, in der dritten Zeile geben Sie den gewünschten Durchmesser ein. Durch Betätigen der Taste "->ca1" ("->ca2") führen Sie die Änderung vom Kopfspiel für das Ritzel (Rad) durch.
In diesem Absatz ist die minimale Zahnanzahl angeführt, die bei der Nullkorrektur verwendet werden kann, ohne dass Zahnunterschneidung oder Zahnverjüngung eintreten würden.
Es handelt sich um die Parameter, die über die Qualität der entworfenen Verzahnung informieren. Es ist zweckdienlich, deren Werte mit den empfohlenen Werten zu vergleichen.
Für einen stetigen Getriebeeingriff ist es nötig, dass bevor das eine Paar der miteinander eingreifenden Zähne aus dem Eingriff herauskommt, das andere Paar schon in den Eingriff eingeht. Der Eingriffsfaktor in der Stirnebene (linke Spalte) informiert, wie viele Zähne zur selben Zeit gemeinsam eingreifen. Der Wert ea=1 entspricht dem Grenzfall, wo sich nur ein Paar dauernd im Eingriff befindet. Beim Wert
Nach den Anforderungen des Getriebes sollte dieser Parameter nicht 1.1 - 1.2 unterschreiten.
Es ist die Summe des Eingriffsfaktors in der Stirnebene und des Eingriffsfaktors in der Achsenebene.
Für dessen Bestimmung gelten dieselben Empfehlungen wie für
Auf den Zeilen [8.7 - 8.10] können Sie die Abmessungen der einzelnen Räder genauer definieren. Nach dem Entfernen des Hakens an der Taste auf Zeile [8.7] können Sie die entsprechenden Abmessungen nach der Abbildung im Kopf dieses Absatzes definieren. Durch Drücken der Taste "<=" [8.7] füllen Sie die voreingestellten Werte aus.
Die Form der einzelnen Räder wird nach der Definition angezeigt. Falls die Innenabmessungen vom Rad nicht definiert sind, wird in der Berechnung mit Rädern als volle Zylinder gerechnet.
Die Anwendung vom "Automatischen Entwurf" [2.10], Verzahnungsentwurf [4.4] und Berechnung des genauen mn [4.6] hebt die Raddefinition auf und benutzt die vollen Zylinder.
Ist auf Grund der übertragenen Leistung, Belastungsart und Ritzelmaterials geschätzt. Er dient lediglich zur Orientierung beim Entwurf der Radabmessungen.
Richtwert, der vom Mindestdurchmesser der Welle abgeleitet ist.
Dieser Parameter teilt mit, welches Verhältnis zwischen dem Fußkreisdurchmesser und dem inneren Durchmesser des Zahnkranzes di/df (Abb. 8.3) besteht. Er nimmt Werte im Bereich 0-100% auf. Im Falle, dass das ausgewertete Rad hergestellt wird als eine Vollscheibe (ohne Entlastungen) ist der Parameterwert = 0. Dieser Parameter beeinflusst die Berechnung der kritischen Drehzahl der Getriebe.
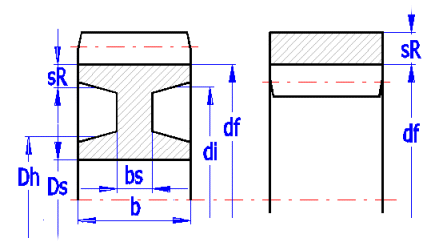
Wird als Summe der einzelnen Zylinderteile gerechnet (Zahnkranz, Hauptfuß, Nabe). Falls der Entlastungsfaktor di/df=0 ist, wird das Radgewicht als Gewicht eines vollen Zylinders gerechnet (was in den meisten Fällen ausreichend ist). Es dient zu einer schnellen Orientierung beim Entwurf.
Das ist ein weiterer qualitativer Parameter, der die verlangte Getriebegenauigkeit [2.6] und den Typ der Schmierung beeinflusst
(Räderschmierung).
ist eine Drehzahl, bei der die Drehgeschwindigkeit mit der eigenen Winkelfrequenz der Getriebeschwigungen identisch wird.
Es ist der Quotient der Ritzeldrehzahl und der "Kritischen Drehzahl".
Wenn das entworfene Getriebe im Bereich der kritischen Drehzahl arbeitet (N ~ 1), wird das Resonanzverhältnis N als eine rote Zahl angezeigt. In diesem Fall sollten Sie Anpassungen des entworfenen Getriebes (eine Zahnzahländerung) durchführen, eventuell einen Spezialisten konsultieren.
Eine genaue Bestimmung des Verlustfaktors ist schwierig. Deshalb ist hier eine annähernde aus der Zahnanzahl, dem Eingriffsfaktor, dem Beta-Winkel und dem Reibungskoeffizienten ausgehende Berechnung verwendet. Der Reibungskoeffizient ist auf Grund der gewählten Genauigkeitsstufe der Verzahnung [2.6] im Bereich 0.04-0.08 gewählt
Die Berechnung der Koeffizienten erfolgt nach der ISO6336:2006, bzw. nach der AGMA 2001-D04, AGMA 908-B89/95. Details befinden sich im theoretischen Teil, Liste der angewandten Normen und Literatur ist am Ende dieser Hilfe angeführt.
In diesem Teil konkretisieren Sie die Berechnungsarten einiger Koeffizienten. Nach dem Betätigen der Schaltfläche kommt es zur Einstellung der Ausgangswerte, die auf Grund der Erfordernisse aus dem Absatz [2.0] eingestellt sind.
Es stehen drei Berechnungsmethoden zur Verfügung (B2006), (C2006) und (C1996).
Die Methode B eignet sich für alle Typen von Stirnzahnrädern. Sie ist relativ kompliziert und bei einer ungeeigneten Auswahl des Materials und des Genauigkeitsgrades im Hinblick auf die Belastung können die KV-Werte unrealistisch sein. Daher ist es möglich, in der Berechnung die Obergrenze von KV einzustellen (voreingestellt 5.0). Bei deren Überschreitung empfiehlt es sich, das gewählte Material und den Genauigkeitsgrad im Hinblick auf die Verzahnungsbelastung zu überprüfen. Die Methode C kann mit gewissen Einschränkungen angewendet werden (siehe theoretischer Teil).
Es stehen drei Berechnungsmethoden
- Berechnung nach ISO6336-1(2006) ... Detaillierter Faktorentwurf, der alle
Einflüsse enthält (zur Anwendung empfohlen)
- Vereinfachte Berechnung ISO6336 ... Geht aus der ISO6336- Methodik aus,
vereinfacht (eher konservative Werte)
- Vorläufiger Entwurf (Grafik) ... Richtwerte für optimal entworfenes Getriebe
(optimistische Werte)
Diese ist von einer Vielzahl von Faktoren abhängig, und vor allem von
konkreten Abmessungen und der Getriebekonstruktion (siehe theoretischer Teil).
Im Absatz [18.0] können alle diese Parameter detaillierte eingestellt werden.
Bei einer ungeeigneten Wahl der Eingangsparameter können die
Durch Drücken der Taste "=>" gehen Sie zur Berechnung von
Gemäß ISO 6336-5 ist es empfohlen, im Falle einer vollen Reversierung
(eingelegtes Rad, Planetrad, Zahnstange) den Wert
Die Auswahl "Automatisch" wählt nach den ausgewählten Werkstoffen die entsprechende Berechnungsart vom Koeffizienten. Falls gewünscht, können Sie die Berechnungsart direkt durch Auswahl aus der Liste durchführen.
Falls die optimale Modifikation des Zahnprofils im Hinblick auf den Ausschlag
des Zahns bei aktuellem Belastungsniveau angewendet wird, wählen Sie "Optimale
Profilmodifikation" aus. Die Auswahl von diesem Parameter hat Einfluss auf die
Berechnungsart der Koeffizienten
Im Auswahlverzeichnis wählen Sie den Öltyp. Für weniger beanspruchte Getriebe kann Mineralöl gewählt werden, bei höheren Geschwindigkeiten, größeren übertragenen Leistungen und höheren Anforderungen an Effektivität ist der Einsatz von Synthetiköl vorteilhafter.
Einige Vorteile der Synthetiköle
- Verringerung der Gesamtverluste um 30% und mehr
- Verringerung der Arbeitstemperatur des Öls
- Erhöhung des Zeitraums für den Ölwechsel 3-5x (Senkung der Kosten für
Instandhaltung)
Demgegenüber stehen der höhere Preis, die möglichen Probleme mit den Kunststoff-
oder Gummiteilen und die beschränkte Mischbarkeit mit Mineralöl.
Die empfohlene Viskosität wird nach der Härte des Radwerkstoffes und der Umfangsgeschwindigkeit gewählt. Falls Ihnen der empfohlene Wert nicht passt, löschen Sie den Haken an der Taste und geben einen eigenen Wert ein.
Wenn Sie die erste Position aus dem Verzeichnis "Automatic" wählen, wird die von der Genauigkeitsstufe abgeleitete Oberflächenrauhigkeit verwendet. Sie können aber auch den genauen Wert eingeben, wenn Sie diesen kennen.
Berücksichtigt die höhere Traglast für eine begrenzte Anzahl an Belastungszyklen. Der Koeffizient ist von den Interpolationen aus entsprechenden Beschädigungskurven abgeleitet (ISO6336, AGMA 2001-D04). Für die Anzahl der Zyklen N=1010 (gekennzeichnet als ∞) wird der Wert des Koeffizienten zwischen den Werten 0.85 bis 1.00 gewählt. Für einen kritischen Betrieb wird der Wert 0.85 gewählt, bei gesicherter optimaler Schmierung, Werkstoffes, Herstellung und Erfahrung kann der Wert 1.00 angewendet werden.
Eine Kerbe im Zahnrad (z. B. eine Schleifkerbe im Zahnübergang in der Nähe des kritischen Querschnitts) erhöht i. d. R. den Wert der Spannungskonzentration verursacht durch den Fußübergang, sodass der Spannungskonzentrationsfaktor entsprechend höher ist. Falls sich die Kerbe nahe am kritischen Schnitt befindet, wird dann der Koeffizient YS mit dem Koeffizienten YSg ersetzt.
Beim Setzen des Hakens an der Taste wird der Wert des Koeffizienten YS mit dem Wert von YSg ersetzt. Die Werte des Koeffizienten YSg werden im Absatz [18.0] berechnet, in den durch Drücken der Taste "=>" umschalten.
In diesem Teil sind die Berechnungsarten von einigen Koeffizienten zu konkretisieren. Nach dem Drücken der Taste kommt es zur Einstellung der Originalwerte, die auf Grund der Anforderungen aus dem Absatz [2.0] eingestellt sind.
Nach ANSI/AGMA 2001--D04 ist es empfohlen, im Falle einer vollen Reversierung
(eingelegtes Rad, Planetrad) den Wert
Nach AGMA 2001-D04 wird für N=1010 und für geläufige Nutzung der Wert YN=0.9, ZN=0.85, für kritische Anwendungen dann der Wert YN=0.8, ZN=0.68 gewählt.
In diesem Absatz sind alle notwendigen Werte der Spannung (Biegung, Berührung) für die Berechnung der Sicherheitsfaktoren angeführt.
Üblich werden zwei grundlegende Festigkeitsberechnungen durchgeführt und zwar für die Biegung und Berührung (Kontakt). In dieser Berechnung werden folgende Sicherheitsfaktoren berechnet:
Als Ausgangswert des Sicherheitskoeffizienten kann verwendet werden:
Die Sicherheitskoeffizienten können von Ihnen gemäß der allgemeinen Empfehlungen für die Wahl der Sicherheitskoeffizienten und eigenen Erfahrungen nachbehandelt werden.
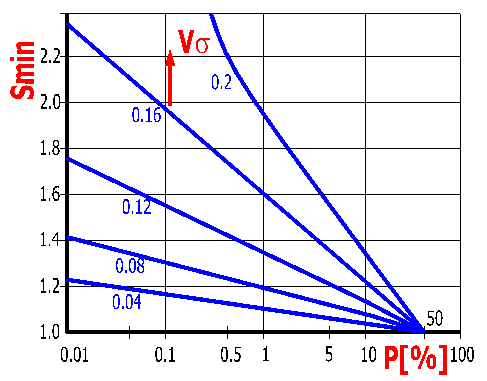
Diese ist nach dem Drücken der Schaltfläche "Calc" berechnet. Der Parameter gibt die Wahrscheinlichkeit an, mit der ein Ausfall des Getriebes eintritt. Dieser geht aus dem Diagramm hervor (siehe Abbildung). Die Wahrscheinlichkeit einer Störung ist eine Funktion des Sicherheitsmaßes Smin [10.1, 10.2] und des Variationsfaktors Vs [10.5].
Bei üblichen Getrieben sollte sich die Berechnungswahrscheinlichkeit einer Störung um 1% bewegen, bei wichtigen Getrieben sollte sie 0.1- 0.01% unterschreiten, (bei sehr wichtigen Getrieben noch weniger).
In diesem Absatz sind Kontrollverzahnungsmaße, Einstellung Korrektion für deren Erreichen und die Formtoleranzen nach ISO 1328 / ANSI/AGMA 2015-1-A01, 2015-2-A06 angeführt.
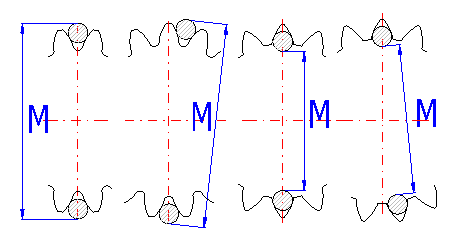
In diesem Absatz sind zwei grundlegende
Kontrollmaße der Verzahnung angeführt. Es handelt sich um das Zahnweitenmaß W
[11.4] und Rollen- und Kugelnmaß M [11.7]. Nach Ankreuzen des Ankreuzfeldes
rechts vom Wert der Zähnezahl, über die gemessen wird [11.3] und vom Wert des
Durchmessers der Rolle/Kugel [11.6], können Sie eigene Werte eingeben. Weitere
für Herstellung der Verzahnung nötige Kontrollmaße hängen sehr eng mit der
Passung der Zahnräder und dem Herstellungsverfahren zusammen, und es ist also
eine enge Zusammenarbeit des Konstrukteurs mit dem Technologen sehr ratsam.

Falls Sie versuchen, die Parameter eines unbekannten Rades zu ermitteln, kann man dieses Instrument anwenden. Am Rad messen Sie das jeweilige Kontrollmaß ab, geben es in das entsprechende Eingangsfeld ein und die Formel führt die Korrekturmodifikation x1 (SumX) so durch, dass das gemessene Maß W oder M mit dem Messwert übereinstimmt.
In diesem Teil ist die komplette Berechnung von Toleranzabweichungen nach ISO 1328 (ANSI/AGMA 2015-1-A01) angeführt. Die Abweichungsberechnung ist mit der Hauptberechnung verbunden und die Abweichungen werden für den aktuellen Genauigkeitswert, das Modul und die Raddurchmesser und –breiten berechnet. Die Abweichungswerte werden anschließend bei der Berechnung der Sicherheitsfaktoren angewendet.
Falls Sie unabhängig von der aktuellen Berechnung die Abweichungen für andere Verzahnungsabmessungen berechnen wollen, entfernen Sie den Haken an der Taste auf Zeile [11.14]. Die Farbe der Eingangszellen [11.15, 11.16, 11.17] ändert sich auf weiß und Sie können eigene Werte der Verzahnungsabmessungen eingeben.
d: 5
b: 4
Verzahnungsqualität A2 - A11
0.5 ≤ mn ≤ 50
5 ≤ z ≤ 1000 oder 10000/mn was auch immer weniger ist
5 ≤ dT ≤ 10000 mm
f'isT, F'isT: 5≤ dT ≤2500 mm
FbT: 5 ≤ dT ≤ 4000 mm; 4 ≤ b ≤ 1000 mm
0.2 ≤ mn ≤ 5
2 ≤ d ≤ 1000 mm
3 ≤ z ≤ 1000
β ≤ 45°
FrT: 0.5 ≤ mn ≤ 50; 5 ≤ d ≤ 12000 mm
Verzahnungsqualität Q: 4-10
mn: 0.2
d: 5
Im belasteten Getriebe entstehen Kräfte, die in den Bau der Maschine übertragen werden.
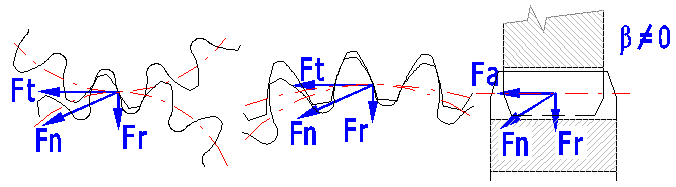
Bei einer Schrägverzahnung entsteht ein zusätzliches Biegemoment, das bei dem Wellenentwurf zu berücksichtigen ist.
Das ist ein weiterer qualitativer Parameter, der die verlangte Getriebegenauigkeit [2.6] und den Typ der Schmierung beeinflusst
(Räderschmierung).
Dies ist eine weitere qualitative Kennzahl, die bei der Berechnung des " Ungleichmäßigkeitsfaktors der Zahnbelastung" verwendet ist.
In einer überwiegenden Mehrheit von Fällen ist der Achsabstand kein Ergebnis der Verzahnungsberechnung, sondern es handelt sich um einen der Eingangsparameter, der dringend einzuhalten ist. Oft wird der Achsabstand auch aus einer genormten Reihe gewählt. Es ist möglich, den verlangten Achsabstand auf zwei Weisen zu erreichen, und zwar:
| ID | Laufende Nummer |
| z1/ |
Anzahl der Zähne des Ritzels |
| z2/N2 | Anzahl der Zähne des Rades |
| i | Übersetzungsverhältnis |
| b | Schrägungswinkel |
| S x | Summe der Einheitsverschübe |
Der Achsabstand wird in diesem Falle lediglich durch die Einstellung des Einheitsverschubes vom Ritzel beeinflusst (fïr die Zahnstange beträgt er x2=0). Auf der Zeile [14.1] sind der aktuelle Achsabstand aw und der Bereich der Achsabstände angeführt, die man durch die Änderung x1 erreichen kann.
Auf der Zeile [14.2] geben Sie den gewünschten Achsabstand ein. Durch Drücken der Taste "->x1" führen Sie die Änderung des Einheitsverschubes vom Ritzel durch.
Dieser Absatz erlaubt eine Orientierungsberechnung der Verlustwärme und der für deren Abfuhr benötigten Gehäuseoberfläche.
Die Öltemperatur im Gehäuse sollte sich im Bereich 50-80 °C bewegen, für kleinere Module sollte sie niedriger sein. Eine genauere Temperaturfestlegung ist von dem gewählten Bau und den verwendeten Werkstoffen abhängig. Bei einer höheren Öltemperatur entsteht die Gefahr der Herabsetzung des Flankenspieles in der Verzahnung, und es könnte zu einer Verzahnungsverreibung kommen.
Dieser ist von dem Bau und dem Umfeld des Getriebes abhängig. Vorläufig kann gewählt werden:
für ISO:
für ANSI:
Diese ist von der übertragenen Leistung und der Verzahnungseffizienz abhängig.
Der Parameter gibt die minimale nötige Gehäuseoberfläche für die Abfuhr der Verlustleistung und Erhaltung der verlangten Öltemperatur an .
In diesem Absatz sind die Wellendurchmesser (Stahl) entworfen, die den verlangten Belastungen entsprechen (übertragene Leistung, Drehzahl). Diese Werte dienen nur als Orientierungswerte, für den Finalentwurf ist es geeignet, eine genauere Berechnung zu verwenden.
In der Praxis kommt oft die Situation vor, dass Sie vor eine unbekannte Verzahnung gestellt werden, deren Parameter zusätzlich berechnet werden müssen (Konkurrenzvergleich, Herstellung eines Ersatzrades ....). Deshalb gibt es hier ein einfaches Werkzeug, das die primäre Berechnung des ursprünglichen Parameters - des Moduls erleichtern sollte.
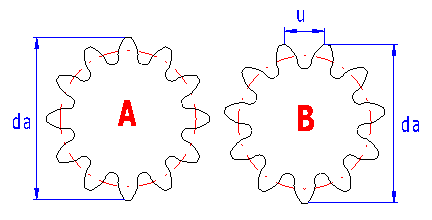
Es ist offensichtlich, dass das angeführte Verfahren eine bestimmte Praxis und Erfahrung erfordert, nichtsdestoweniger bei üblichen Verzahnungen, bei denen es vorausgesetzt werden kann, dass sie mit üblichen genormten Werkzeugen und Vorgängen hergestellt wurden, führt es im Ganzen verläßlich zu vernünftigen Ergebnissen.
In diesem Absatz stehen Hilfsberechnungen zur Verfügung. Bei der Werteingabe dieselben Einheiten verwenden wie in der Hauptberechnung. Die Übertragung der eingegebenen und berechneten Werte in die Hauptberechnung durch Drücken der Schaltfläche "OK" durchführen.
Die Berechnung von KHb und YSg ist nachstehend beschrieben.
Die Berechnung von KHb besteht aus mehreren, nacheinander folgenden Schritten.
1) Berechnung fsh = f(Fm, dsh, K',
l, s, b1,
d1)
2) Berechnung fma = f(fHb1
, fHb2)
... [11.29]
Aus den Werten fsh und fma (ggf. fsh2, fca, fbe) wird der Wert Fbx
berechnet
3) Berechnung Fbx
= f(fsh, fma, fsh2, fca, fbe, B1, B2)
4) Berechnung yb
= f(Fbx, sHlim)
5) Berechnung Fby
= f(Fbx,
yb)
6) Berechnung KHb = f(Fby,
Fm,
cgb,
b)
Eine Vielzahl von Koeffizienten kann durch einige Methoden definiert werden, und eine gute Kenntnis des entworfenen / kontrollierten Getriebes ist notwendig. Für einen Basisentwurf drücken Sie die Taste "Ausgangswerte einstellen". Damit stellen Sie die Berechnung in den Basiszustand wie folgt ein:
- [18.8] ... eingestellt nach Wahl [2.5]
- [18.9, 18.10] ... Abmessungen geschätzt auf Grund der Getriebegröße und
Einstellung von [18.8]
- [18.16, 18.17] ... eingestellt nach gewähltem Genauigkeitsgrad [2.6]
Danach können Sie schrittweise diejenigen Parameter eingeben und einstellen, die Sie kennen oder abschätzen können.
Eigene Werte können Sie nach dem Entfernen vom Haken im Hakenfeld des jeweiligen Eingangs eingeben.
Es ist der Wert voreingestellt, der aus dem Fußdurchmesser des Ritzels und dem Mindestdurchmesser der Welle [8.4] ausgeht. Falls Sie den Wellendurchmesser kennen, entfernen Sie den Haken an der Hakentaste und geben Sie den eigenen Wert ein.
Hier ist der Verzahnungstyp zu wählen.
Wählen Sie aus der Liste die entsprechende Lagerung des Ritzels nach der Abbildung aus. Voreingestellt ist nach [2.5].
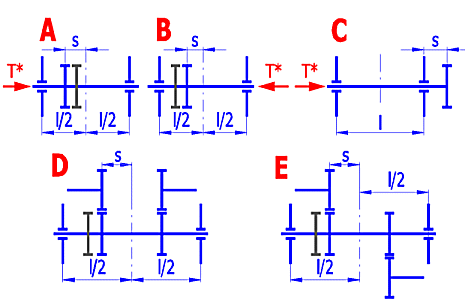
Vorläufig wird der Wert l und s von der Radbreite und der eingestellten Speicherung des Getriebes [18.8] abgeleitet. Nach dem Entfernen vom Haken können Sie eigene Werte eingeben.
Die Werte fsh, fsh2, fma, fca, fbe beschreiben die Verformungen von Zahnrädern, deren Abweichungen und die Lagerungsabweichungen. Die Werte fsh2, fca und fbe werden in dieser Berechnung nicht behandelt, und falls Sie keine komplette Gleichung für die Berechnung von Fbx [18.17] rechnen, können sie gleich Null sein. Die Werte fsh und fma können Sie direkt eingeben, oder die aus den Parametern der vorgenannten Zeilen berechneten Werte.
Wählen Sie aus der Liste die entsprechende Modifikation der Zahnschrägung aus. Details sind in der ISO6336:1(2006) angeführt.
In der Liste wählen Sie die Berechnungsart von Fbx aus.
1. Eigene Werte
2. Radpaare ohne Nachweis von Gröse und günstiger Lage des Kontakttragbildes und
ohne optimales Lasttragbild
3. Radpaare mit Nachweis von günstiger Lage des Kontakttragbildes (z.B. durch
Anpassen der Verzahnung Oder Einstellen der Lager)
4. Wenn außer Ritzelkörper- und Ritzelwellen- verformungen auch Rad- und
Radwellenver- formungen, Gehäuseverformungen und Lager- verformungen zu
berücksichtigen sind.
Zurück zum Absatz [9.0] gelangen Sie durch Drücken der Taste "OK". Die gleichzeitig ist die Berechnung von KHb in der Koeffizientenberechnung nach ISO6336 eingestellt.
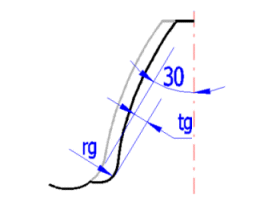
Eine Kerbe im Zahnrad (z. B. eine Schleifkerbe im Zahnübergang in der Nähe des kritischen Querschnitts) erhöht i. d. R. den Wert der Spannungskonzentration verursacht durch den Fußübergang, sodass der Spannungskonzentrationsfaktor entsprechend höher ist. Falls sich die Kerbe nahe am kritischen Schnitt befindet, wird dann der Koeffizient YS mit dem Koeffizienten YSg ersetzt.
Füllen die Kerbenparameter laut Abbildung aus. Nach dem Drücken der Taste "OK" schalten Sie zurück zum Absatz [9.0] um und der Koeffizient YS wird durch den Koeffizienten YSg ersetzt.
Wählen Sie aus der Liste den Materialtyp aus, für den Sie die Materialeigenschaften bestimmen wollen.
Die angewendeten Beziehungen sind für drei Stufen der Materialqualität ML, MQ
und ME bestimmt
- ML stellt die geringsten Anforderungen an die Materialqualität und an seinen
Wärmebehandlungsprozess während der Zahnradherstellung dar.
- MQ stellt die Anforderungen dar, die ein erfahrener Hersteller bei
vernünftigen Herstellungskosten erfüllen kann.
- ME stellt die Anforderungen dar, die im Falle einer hohen Betriebssicherheit
erfüllt sein müssen.
(Für AGMA Stufe 1-3, detaillierte Beschreibung in der Norm.)
Geben Sie die Oberflächenhärte ein. Auf Grund des Materialtyps und seiner Härte werden seine Parameter bestimmt. Am Ende der Zeile ist der Härtebereich angeführt, für den die Parameterberechnung gültig ist. Zur Eingabe der Härte können Sie zwischen verschiedenen Einheiten wählen, und zwar HV, HB und HRC.
Falls Sie eigene Materialwerte eingeben und Material in die Materialtabelle hinzufügen, wählen Sie die richtige Bezeichnung (Art der Wärmebehandlung, nach ANSI/AGMA). Nach dieser Kennzeichnung werden dann in der Festigkeitsberechnung einige Koeffizienten gewählt.
Nach dem Entfernen vom Haken auf der Zeile [19.5] kann man eine eigene Materialbeschreibung eingeben, die in der Materialtabelle angeführt wird und nach der Sie das Material im Absatz [2.0] auswählen werden.
Wählen Sie aus der Liste eine der 5 Zeilen, die für benutzerdefinierte Werkstoffe bestimmt sind. Bei der Übertragung der Werte wird der ursprüngliche Inhalt in der Materialtabelle ohne Warnung überschrieben.
Bei der Entscheidung über eine Schmierungsart der Verzahnung sich nach der folgenden Tafel richten.
| Typ der Schmierung | Umfangsgeschwindigkeit in | |
| [m/s] | [Fuß/min] | |
| Tauchbadschmierung | < 12 | < 2400 |
| Drucköl-Schleuderschmierung | > 12 | > 2400 |
| Ölnebelschmierung | > 60 | > 12000 |
Die Informationen über die Möglichkeiten der 2D- und 3D-graphischen Ausgabe und die Informationen über das Zusammenwirken mit den 2D- und 3D CAD-Systemen finden Sie im Dokument "Grafische Ausgabe, CAD - Systeme".
1. In der Auflistung "Ausgabe der 2D - Zeichnung in" das Ziel - CAD - System (Zielprogramm) auswählen, in welches sie eine Abbildung generieren lassen wollen oder "DXF Datei" für die Herstellung der Zeichnung in die Datei des Formats DXF.
2. In der Auflistung "Maßstab der 2D - Zeichnung" den Zeichnungsmaßstab einstellen. Die Zeichnung ist immer im Maßstab 1:1 hergestellt. Durch den Maßstab stellen Sie nur bestimmte Zeichnungsparameter ein, z. B. eine Textgröße, einen Wert des Überhangs der Achsen.
3. Wenn es nötig ist, sind auch weitere Steuerungselemente einzustellen. Die meisten Berechnungen beinhalten auch weitere Einstellungsmöglichkeiten, die von der Berechnung und dem gezeichneten Objekt abhängig sind. Eine Erläuterung dieser Ergänzungsoptionen finden Sie in der Hilfe der entsprechenden Berechnung.
4. Starten Sie durch das Drücken der Schaltfläche Zeichnen mit der Ikone der verlangten Zeichnung.
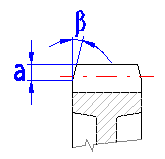
Der Winkel stellt die Andrehung der Gesamtzeichnung der Räder bezüglich der Horizontalachse (Abbildung - siehe Schaltfläche) ein .
Durch diese Parameter Abschrägung des Zahnrades nach der Abbildung einstellen .
Außer der Standarddarstellung, die in den Zusammenstellungs- und Detailzeichnungen verwendet wird, können auch detaillierte Zahnabbildung, Detail des ganzen Rades, Abbildung des Radeingriffes und der Werkzeugszeichnung aufgezeichnet werden. Die Zahnflanke ist aus der Simulation des Werkzeugseingriffs mit dem bearbeiteten Rad berechnet, was die genaue Zahnform einschließlich des Zahnfußes ermöglicht festzustellen. Die Detailzeichnung des ganzen Rades kann dann als Unterlage zur Verfertigung eines genauen Modells in 3D-CAD-System, oder als Eingangsangaben für die Radherstellung dienen.
Auf dem Blatt "Koordinaten" sind in einer Tabelle die Koordinaten der Punkte der rechten Seite der Zahnkurve (Ritzel und auch Rad) im Koordinatensystem X, Y mit dem Punkt 0,0 im Radmittelpunkt. Zur Umrechnung und Generierung der aktuellen Koordinaten nach der Einstellung vom Absatz [20] die Taste "Auffrischen" betätigen.
Das Herstellungswerkzeug (B), dessen Maße im Absatz [3] definiert sind, wird stufenweise nach dem Kreis (C) mit einem Winkelschritt W abgewälzt und generiert so die Zahnkurve (A) in einzelnen Punkten (2).
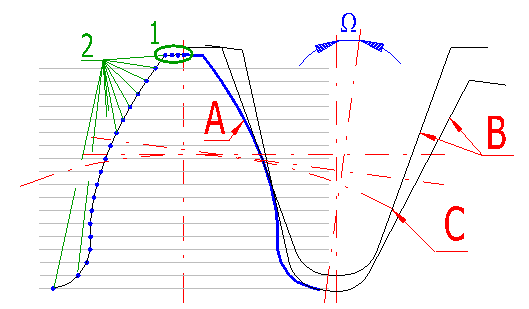
Hier ist die Zahnanzahl einzugeben, die in der Zeichnung in der teilweisen Aufzeichnung durchgeführt werden sollen. Die Ritzelzähne sind in der Richtung nach oben, die Radzähne in der Richtung nach unten aufgezeichnet, immer symmetrisch zur vertikalen Achse. In der Abbildung sind 3 Zähne für das Ritzel ausgewählt (das untere Rad) und für das Rad 4 Zähne.
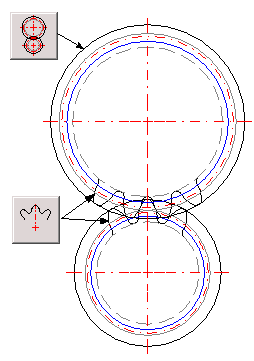
Sie definiert die Anzahl der Punkte (Abschnitte) auf dem Kopf der Zahnhälfte
siehe Abbildung [20.4], Verweisung (1).
Bereich der zugelassenen Werte: <2 - 50>, empfohlene: 5
Sie definiert die Anzahl der Punkte (Abschnitte), die die komplette
Zahnflanke bilden, siehe Abbildung [20.4], Verweisung (2).
Bereich der zugelassenen Werte: <10 - 500>, empfohlene: 30 und mehr
Sie definiert den Winkelzuwachs, nach dem sich das Werkzeug bei der
Bearbeitung der Zahnflanke abwälzt (verdreht), siehe Abbildung [20.4], Winkel W.
Bereich der zugelassenen Werte: <0.02 - 10>, empfohlene: 0.5
Sie definiert, wie viele Stellungen bei der Zahneingriffsaufzeichnung
dargestellt werden.
Bereich der zugelassenen Werte: <3 - 100>, empfohlene: 20
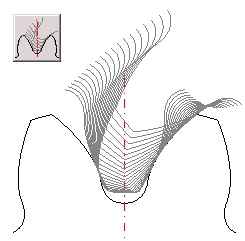
Weil es bei der inneren Verzahnung nötig und ratsam ist, nicht nur den Eingriff der eigenen Zähne sondern auch mögliche Zahnkollisionen zu kontrollieren, ist die Zeichnung des kompletten Eingriffs des äußeren und inneren Rades im Fall der inneren Verzahnung zu generieren. Die Anzahl der Zahnkopien bei der Eingriffskontrolle [20.9] gibt in diesem Fall die Zahl der Ritzelkopien an.

Sie gibt die Verdrehung des Ritzels zwischen den einzelnen Ritzelkopien an, die bei der Eingriffskontrolle generiert wurden.
Der Umschalter "Zeichnung ohne Mittellinien" definiert, ob die Mittellinien in der eingefügten Zeichnung entfernt werden sollen.
3D-Modell-Beispiel


Den Text der Beschreibung platzieren Sie in eine 2D-Zeichnung durch
Betätigung der Schaltfläche "Vykreslit – Aufzeichnen". Den Text können Sie nach
dem Ankreuzen eines Ankreuzfeldes aufbereiten.
Wenn es das entsprechende Modul für das Einfügen der Modelle in das 3D CAD
System unterstützt, ist der Inhalt der einzelnen Zeilen in die Benutzerattribute
des Modells eingefügt und kann für die Generierung der Stückliste verwendet
werden. (Einzelheiten finden Sie in der Hilfe für den
Anschluss an das zugehörige 3D CAD System.)
Eine Reihe von Berechnungen (Verzahnung, Federn…) ermöglicht es, in die Zeichnung auch eine zugehörige Tabelle mit Textinformationen über das berechnete Objekt einzufügen. Die Tabelle wählen Sie von der entsprechenden Auflistung aus (im Falle, dass die Berechnung das Einfügen von mehreren Typen ermöglicht). Die Aufzeichnung der Tabelle durch Betätigung der Schaltfläche „Tabelle zeichnen“ starten.
Die Möglichkeit der Generierung des Zahnradprofils als Folge von Strecken (DXF) wurde um die Möglichkeit der Generierung der Steuerkurven erweitert, welche die Seiten des Zahns definieren und es möglich machen, glatte (extrapolierte) Kurven im jeweiligen CAD-System zu erstellen. Dies ermöglicht die Erstellung von zwar nicht-parametrischen, jedoch genauen 3D-Modellen der Verzahnung.
Die Erstellung eines genauen Modells besteht so aus drei einfachen Operationen:
Allgemeines Verfahren:

Für die absolute Mehrheit der stirnverzahnten Räder ist ein Eingriffswinkel ausreichend, der für die eingreifende und nicht eingreifende Seite identisch ist. Für einige Anwendungen kann es jedoch von Vorteil sein, einen abweichenden Eingriffswinkel zu wählen. Nach Markieren der Taste rechts können Sie so unterschiedliche Eingriffswinkel für jede Zahnseite eingeben.
Gibt an, wie viele Punkte generiert werden, welche die Kurve der Zahnseite definieren. In der Regel ist der Wert 20 geeignet. Für spezielle Fälle (Einschränkung des CAD-Systems, Genauigkeit ...) können die Werte 12–200 verwendet werden.
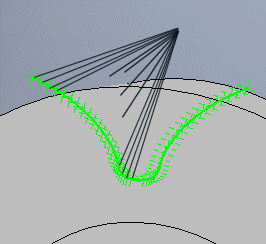
Fügt über das generierte Profil der Lücke zwischen den Zähnen hinaus ein weiteres Stück hinzu, das für die bessere Auswahl der Kurven geeignet sein kann oder dessen Existenz für die korrekte Interpretation der Kurven notwendig ist.
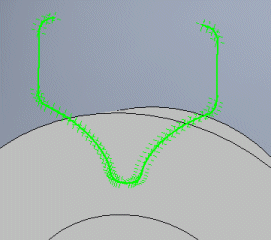
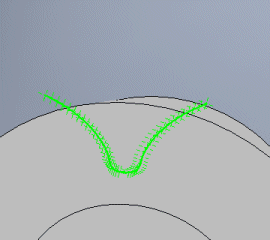
Gibt die Anzahl der Punkte an, die für die Rundung der Anbindung und des Abschlusses des Überbaus verwendet werden. In den meisten Fällen reicht der Wert 5.
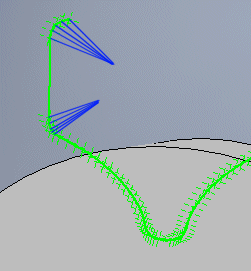
Einige CAD-Systeme erfordern ein abgeschlossenes Profil, andere erfordern ein offenes oder manuell abgeschlossenes Profil. Der Schalter verbindet / verbindet nicht den ersten und den letzten Punkt.

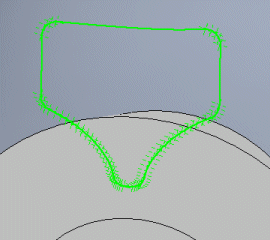
Verschiedene CAD-Systeme unterstützen den Import der die Kurven bildenden Punkte in verschiedenen Formaten. Zur Verfügung stehen die Formate:
Fügt in jeden Punkt der Kurve einen kleinen Kreis ein. Geeignet im Falle, wenn das CAD-System nur das DXF-Format einzulesen vermag und es notwendig ist, das Profil Punkt für Punkt manuell zu erstellen.
Höhe der imaginären Walze (Teilkreisdurchmesser), auf welcher gerade eine Umdrehung der Rotation erfolgt. Diese Angabe ist meistens für die Rotation mit Extrudieren in 3D CAD einzugeben.
In der Zeile sind in verkürzter Form die Parameter der Verzahnung angeführt, die vollständig die Geometrie und wichtige Abmessungen definieren.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
Warmbehandlungsverfahren
1...Nicht wärmebehandelt, normalgeglüht
2...Vergütet
3...Zementiert, gehärtet, außen gehärtet
4...Nitriert
ISO 6336-1:2006
- Calculation of load capacity of spur and helical gears - Part 1: Basic
principles, introduction and general influence factors
- Calcul de la capacité de charge des engrenages cylindriques a dentures droite
et hélicoidale - Partie 1: Principles de base, introduction et facteurs généraux
d'influence
- Výpočet únosnosti čelních ozubenych kol s přímými a šikmými zuby - Část 1:
Základní principy, doporučení a obecné ovlivfňující faktory
ISO 6336-2:2006
- Calculation of load capacity of spur and helical gears - Part 2: Calculation
of surface durability (pitting)
- Calcul de Ia capacité de charge des engrenages cylindriques à dentures droite
et hélicoidale - Partie 2: Calcul de la résistance à la pression de contact (piqure)
- Výpočet únosnosti čelních ozubených kol s přímými a šikmými zuby - Část 2:
Výpočet trvanlivosti povrchu (pitting)
ISO 6336-3:2006
- Calculation of load capacity of spur and helical gears - Part 3:
Calculation of tooth bending strength
- Calcul de la capacité de charge des engrenages cylindriques à dentures droite
et hélicoïdale - Partie 3: Calcul de la résistance à la flexion en pied de dent
- Výpočet únosnosti čelních ozubených kol s přímými a šikmými zuby - Část 3:
Výpočet pevnosti v ohybu zubu
ISO 6336-5:2003
- Calculation of load capacity of spur and helical gears – Part 5: Strength and
quality of materials
- Calcul de la capacité de charge des engrenages cylindriques à dentures droite
et hélicoïdale – Partie 5: Résistance et qualité des matériaux
- Výpočet únosnosti čelních ozubených kol s přímými a šikmými zuby – Část 5:
Údaje o pevnosti a kvalitě materiálů
ISO 1265
- Metalic materials - Conversion of hardness values
- Matériaux métalliques - Conversion des valeurs de dureté
- Metallische Werkstoffe - Umwertung von Hartewerten
- Kovové materiály - Převod hodnot tvrdosti
ISO 1328-1:1997
- Cylindrical gears - ISO system of accuracy - Part 1: Definitions and allowable
values of deviations relevant to corresponding flanks of gear teeth
- Engrenages cylindriques - Systéme ISO de precision - Partie 1: Définions et
valeurs admissibles des écarts pour les flanc homologues de la denture
- Toleranzensystem ISO - Teil 1: Toleranzen fur Flankenlinienabweichungen
- Čelní ozubená kola - Soustava přesnosti ISO - Část 1: Definice a mezní úchylky
vztažené na stejnolehlé boky zubů ozubeného kola.
ISO 1328-2:1997
- Cylindrical gears - ISO system of accuracy Part 2: Definitions and
allowable values of deviations relevant to radial composite deviations and
runout information
- Engrenages cyindriques - Systéme ISO de precision Partie 2: Definitions et
valeurs admissibles des ecarts composés radiaux et information sur le faux-rond
- Čelní ozubená kola - Soustava přesnosti ISO - Část 2: Definice a hodnoty
dovolenych úchylek relevantní k radiálním kinematickým úchylkám a informativně k
obvodovému házení.
ISO 1122-1:1998
- Vocabulary of gear terms - Part 1: Definitions related to geometry
- Vocabulaire des engrenages - Partie 1: Définitions géométriques
- Slovník termínů ozubení - Část 1: Definice vztahující se ke geometrii
ANSI/AGMA 2001-D04
AMERICAN NATIONAL STANDARD Fundamental Rating Factors and Calculation Methods
for Involute Spur and Helical Gear Teeth
AGMA 908-B89
Geometry Factors for Determining the Pitting Resistance and Bending Strength of
Spur, Helical and Herringbone Gear Teeth
ANSI/AGMA 2015- 1-A01
Accuracy Classification System - Tangential Measurements for Cylindrical Gears
ANSI/AGMA 2015-2-A06
Accuracy Classification System - Radial Measurements for Cylindrical Gears