The calculation is designed for geometric and strength design and check of spur gearing with straight and helical toothing (external, internal gear rack). The application provides solutions for the following tasks.
The calculations use procedures, algorithms and data from standards ANSI, ISO, DIN, BS and specialized literature.
List of standards: ISO 6336, ISO 1328, DIN 3990,
User interface.
Download.
Purchase, Price list.
Information on the syntax and control of the calculation can be found in the document "Control, structure and syntax of calculations".
Information on the purpose, use and control of the paragraph "Information on the project" can be found in the document "Information on the project".
The complete text concerning the theory can be found in Involute gearing - theory
Geared transmissions can be divided into:
Power gearing - In case of gearing designed, above all, for a power transmission and transformation, it is necessary to perform a strength design/check (for example, drives of machines, industrial gearboxes, etc.).
Non-power gearing - In case of gearing with minimum transferred torsional moment with respect to the size of the gears, it is not necessary to perform any strength design/check (for example, instruments, regulation devices, etc.).
The task of a spur gearing design cannot be solved directly and allows considerable freedom as far as options of diameter and width parameters of gears. Therefore, it is necessary to proceed iteratively and successively specify the solution and fine-tune the monitored parameters.
This procedure provides a quick preview of parameters of the designed gearing. Although this designed gearing is normally usable, successive optimizing of a series of parameters may quite considerably improve the properties of the designed gearing. Proceed in the design as follows:
Before optimizing parameters, first carry out the "Quick (orientation) design" described above. Then proceed as follows:
The design of gearing with a given axis distance is the most frequent task when designing spur gearing. Proceed in such a design as follows:
When designing non-power gearing, it is not necessary to solve and check any strength parameters. Directly choose, therefore, a suitable number of teeth and the module [4.1, 4.7] and check dimensions of the designed gearing.
Enter basic input parameters of the designed gearing in this paragraph.
Enter the power to the driven gear. Usual values are in the range 0.1-3000 kW / 0.14-4200 HP, in extreme cases up to 65 000 kW /100 000 HP.
Enter the speed of the driven gear. Extreme speed can reach 150 000 rpm. The speed of the driven gear is calculated using the number of teeth of both gears.
This is the result of the calculation and cannot be entered.
The optimum transmission ratio varies in the range 2-8. In extreme cases this ratio can reach up to 20. The transmission ratio can be entered in the left input field using the keyboard. The right pop-up list contains recommended values of the transmission ratio and when selecting a value from this list, the chosen value is added to the field on the left automatically.
As the actual transmission ratio is the ratio of the number of teeth of both gears (integers), the actual transmission ratio will be mostly different from the desired (entered) one. The value of the "Actual transmission ratio" is displayed on the left; the percentage deviation from the desired transmission ratio is displayed on the right. This deviation for the transmission ratio should be in the range:
i = 1 to 4.5 ........... 2.5%
i is greater than 4.5... 4.0%
In the calculation, it is possible to enter the tangential force, which is in principle the force of the gear rack acting on the pinion, and the velocity of the gear force movement (pinion circumferential speed). From these two values, the transmitted power and the pinion torque are calculated. As the gear rack may be used for a range of various design solutions, it is then necessary to calculate (estimate) and transfer the gearing requirements on both these values.
Specify the force acting on the pinion (rack load).
Specify the gear rack movement velocity.
It is calculated from the transferred force and velocity.
Pw [kW] = Ft * v / 1000
It is calculated from the circumferential speed and the pinion diameter.
It is calculated from the power and speed.
When designing power gearing, enter other supplementary operational and production input parameters in this paragraph. Try to be as accurate as possible when selecting and entering these parameters as each of them may dramatically affect the properties of the designed gearing.
The option is performed, above all, according to the following aspects:
Usually the principle that the pinion has to be harder than the gear (20-60 HB) is followed, whilst the difference in hardnesses increases with increasing hardness of the gear and the transmission ratio. For quick orientation, the materials are divided into 8 groups marked with the letters A to H. Perform selection of the material in the pop-up list separately for the pinion and for the gear. In case you need more detailed information on the chosen material, proceed to the sheet "Material".
Materials A,B,C and D, so-called. soft gears - The toothing is produced after heat treatment; these gears are characterized by good running-in, do not have any special requirements for accuracy or stiffness of support if at least one gear is made of the chosen material.
Materials E,F,G and H, so-called. hard gears - Higher production costs (hardening +100%, case hardening +200%, nitriding +150%). Heat treatment is performed after production of toothing. Complicated achievement of the necessary accuracy. Costly completion operations (grinding, lapping) are often necessary after heat treatment.
Own material values - In case you wish to use a material for production of toothing that is not included in the delivered table of materials, it is necessary to enter some data on this material. Proceed to the sheet "Materials". The first 5 rows in the table of materials are reserved for definition of your own materials. Enter the name of the material in the column designed for names of materials (it will be displayed in the selection sheet) and fill in successively all parameters in the row (white fields). After filling in the fields, go back to the sheet "Calculation", choose the newly defined material and continue in the calculation.
Setting of these coefficients substantially affects the calculation of safety coefficients. Therefore, try to enter as accurate a specification as possible when selecting the type of loading. Examples of driving machines:
Setting these parameters substantially affects the calculation of safety coefficients. Therefore, try to enter as accurate a specification as possible when selecting the type of loading. Examples of driven machines:
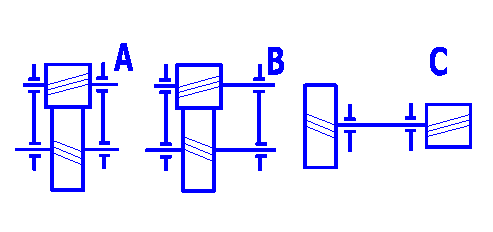
Setting this parameter affects the calculation of the safety coefficient. The type of support defines the coefficient of unevenness of the loading caused, above all, by deflections of the shafts. Choose the type of support according to the following definition and illustration.
Type1:Rigid box, rigid shafts, robust, roller or tapered roller bearings.
Type2:Less rigid box, longer shafts, ball bearings.
When choosing the degree of accuracy of the designed gearing, it is necessary to take into account the operating conditions, functionality and production feasibility. The design should be based on:
The accuracy of toothing is chosen to the necessary extent only, because achievement of a high degree of accuracy is costly, difficult and conditioned by higher demands for technological equipment.
| Degree of accuracy ISO 1328, ANSI/AGMA 2015 |
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Degree of accuracy AGMA |
13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 |
| Max. surface roughness Ra max [nm] | 0.1-0.2 | 0.4 | 0.8 | 1.6 | 1.6 | 3.2 | 6.3 | 12.5 | 25 |
| Max. peripheral speed [m/s] straight teeth | 80 | 60 | 35 | 15 | 8 | 5 | 3 | 3 | 3 |
| Max. peripheral speed [m/s] helical teeth | 100 | 80 | 50 | 30 | 12 | 8 | 5 | 3 | 3 |
|
Specification |
Degree of accuracy ISO 1328 ANSI/AGMA 2015 |
Degree of accuracy AGMA 2000-A88 |
| Control gears | 2 - 4 | 13-12 |
| Measuring instruments | 3 - 6 | 13-10 |
| Turbine reducers | 3 - 5 | 13-11 |
| Aviation reducers | 3 - 6 | 13-10 |
| Machine tools | 3 - 7 | 13-9 |
| Aviation engines | 5 - 6 | 11-10 |
| High speed gearboxes | 5 - 6 | 11-10 |
| Passenger cars | 6 - 7 | 10-9 |
| Industrial gearboxes | 7 - 8 | 9-8 |
| Light ship engines | 7 | 9 |
| Rolling mills, locomotives | 8 - 9 | 8-7 |
| Heavy ship engines, tractors | 8 - 9 | 8-7 |
| Building and agricultural machines | 8 - 10 | 8-6 |
| Textile machines | 7 - 9 | 9-7 |
The coefficient gives the ratio between the maximum (start-up) and nominal torque of the driving machine. The coefficient substantially affects the calculation of the safety coefficient with one-off overloading (start-up) of the gearing. The coefficient can be found in the catalogue of the producer of the driving unit.
Three-phase asynchronous electric motor ... 2-3
The parameter specifies the desired service life in hours. Orientation values in hours are given in the table.
|
Specification |
Durability |
| Household machines, seldom used devices | 2000 |
| Electric hand tools, machines for short-term runs | 5000 |
| Machines for 8-hour operation | 20000 |
| Machines for 16-hour operation | 40000 |
| Machines for continuous operation | 80000 |
| Machines for continuous operation with log service life | 150000 |
Enter the number of tooth load cycles for the pinion and the gear rack.
The recommended values of the safety coefficient vary within the range:
Decide whether you wish to design straight or helical toothing. The following recommendations can be used for your option:
With the "Automatic design" the setting of parameters of the gearing is based on the entered power and operational parameters [1.0; 2.0] and on generally applicable recommendations. Manual optimizing can mostly provide toothing with better parameters (weight, dimensions) or enable modifications of the dimensions based on your own constructional requirements.
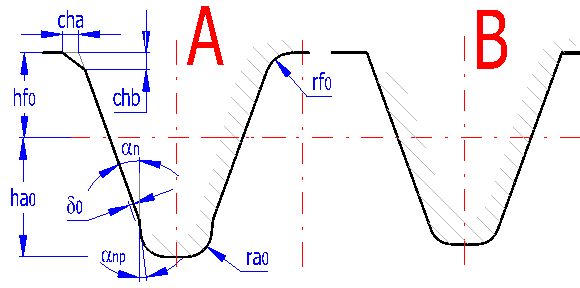
Set the parameters of machining tool and tooth tip relief in this paragraph. The parameters affect most of dimensions of the toothing, tooth shape and the following strength parameters, stiffness, durability, noise, efficiency and others. If you don't know the acurate parameters of the production tool, use the standardized type from the list box on line [3.1], namely:
1. DIN 867 (a=20deg, ha0=1.25, hf0=1.0, ra0=0.38, d0=0, anp=0deg, ca=0.25)
for calculation in SI units and
3. ANSI B6.1 (a=20deg, ha0=1.25, hf0=1.0, ra0=0.3, d0=0deg, anp=0, ca=0.35) for
calculation in inches.
You can define two types of the tool in the form, with protuberance (A) and without protuberance (B). If you define a tool without protuberance, set the protuberance dimension d0=0. Set the tool dimensions according to the dimensions in the picture in the modulus multiples "value"x"modulus" (calculation in SI units) or as a quotient of "value"/"Diametral Pitch" (inch calculation). Choose a pressure angle in paragraph [4]. The base of tooth can be either bevelled or rounded. Therefore choose only one way.
The diagram shows the shape of a tool tooth for wheel/pinion. If you change tool dimensions, press the respective button which will provide redrawing in accordance with the current set values.
An accurate shape of tooth and toothed wheel, check of interferences, etc. is described in the paragraph dealing with graphic output and CAD systems.
Internal toothing is made, in overwhelming majority of cases, by cutting using a circular tool. For the purposes of this calculation we will consider a tool with basic parameters identical with the designed toothing (an0=an, b0=b, mn0=mn). However, angle b cannot be chosen at random when manufacturing the internal toothing, as it is necessary to proceed from the properties of the machine tool and available tools and it is appropriate to consult this selection with a technologist.
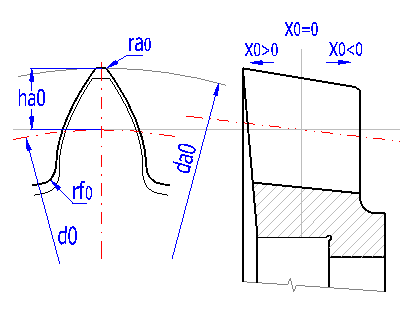
You can see an example of such tool in the picture. The current status of tool sharpening equates its unit correction x0. Resharpening of the tool results in the change of correction and subsequently in the change of tool hub diameter. If the value for correction x0 is unknown, just measure the current hub diameter and use the change of correction x0 [3.13] to adjust the hub diameter da0 [3.14] to a required value.
Due to the manufacturing method and the gear rack geometry, in this case the
tool is an exact negative of the machined gearing (straight teeth). For the
helical teething, the tool is an exact negative of the machined gearing in a
normal section. 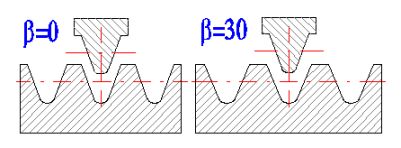
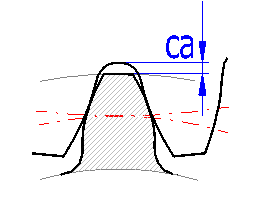
Unit tooth tip relief "ca" affects the diameter of addendum circle. Normally ca=0.25 is chosen which guarantees preventing interference for normally used corrections. If the accurate tool parameters are known, it is possible to choose smaller c*, namely 0.15 to 0.1, and thus achieve increase of profile bite coefficient. Interference can and should be checked on a detailed drawing, see the paragraph dealing with graphic output and CAD systems. Line [3.10] gives minimum tooth tip relief which can be achieved using the selected tool. The selection of smaller tool tip relief is indicated by red colour of input field. Button "<" will transfer the minimum value into the input field. Minimum unit tooth tip relief can be reduced by increasing the height of the tool base.
The geometry of the gearing can be designed in this paragraph. The design of the geometry substantially affects a number of other parameters such as functionality, safety, durability or price.
Enter the number of teeth of the pinion. Additional calculation of the number of teeth of the gear is based on the desired transmission ratio. Determination of the optimal number of teeth is not an unambiguous task and cannot be solved directly. Numbers of teeth affect mesh conditions, noise, efficiency and production costs. Therefore, the number of teeth is chosen and specified according to qualitative and strength indices
A generally applicable rule states that increasing the number of teeth (with the same axis distance) leads to:
A) For both gears annealed normalizationally/improved by heat - soft gears
B) For a hardened pinion and non-hardened gear (or both gears nitrided)
C) Both gears surface hardened
The rule is that higher numbers of teeth are chosen for higher output powers and lower transmission ratios.
The red highlighted text indicates commensurable numbers of teeth, which should be avoided.
This angle determines parameters of the basic profile and is standardized to an angle of 20°. Changes in the
pressure angle a/F affect functional and strength properties. Changes in the meshing angle, however, require non-standard production tools. In case there is no special need to use another meshing angle, use the value of 20°.
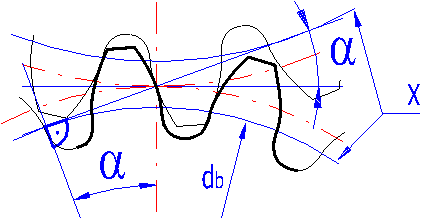
The letter "X" marks the basic circle.
Increasing the meshing angle allows:
Option of values
In case you do not have any special requirements for the designed gearing, it is recommended to use 20°.
Toothing with the slope of teeth = 0 (straight toothing) is used with slow speed and highly loaded gearing. With high speed gearing, where catching of axial forces could be difficult and where increased noise does not cause any problems.
Toothing with the slope of teeth > 0 (helical toothing) is used with high speed gearing; it is characterized by lower noise and higher loading capacity, enabling the use of a lower number of teeth without undercutting.
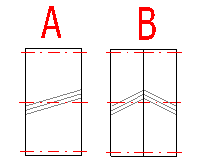
The angle beta is chosen from the sequence 6,8,10,12,15,20 degrees (Fig. A). In case of a double or herringbone gear (Fig. B), values 25,30,35,40 degrees can also be used.
Using the slider, perform setting of a value of the dimensionless coefficient, which specifies the ratio between the pinion width and diameter [4.5].
This parameter can be used to design dimensions of the module, thereby basic geometric parameters of the gear (width, diameter). The recommended maximum value is given in the right column and depends on the chosen material of the gears, their support and transmission ratio of the gearing. Setting this parameter can be done using the slider in row [4.4]. After setting this parameter press the button "Design of toothing". This procedure enables you to design meeting of desired safety level [2.9] and other input parameter requirements.
After processing the "Design of toothing" check the dimensions (widths and diameters of the gears, weight). In case the result is not satisfactory, modify the parameter of the ratio pinion width vs. diameter [4.4, 4.5] and repeat the "Design of toothing".
Lower values - design of a narrower gear, larger module, straight toothing
Higher values - design of a wider gear, smaller module, helical toothing
This is the most important parameter, which determines the size of the tooth and thereby the gearing itself. It is generally applicable that for a higher number of teeth it is possible to use a smaller module (higher value P with a calculation in imperial units) and vice versa. The right pop-up list includes standardized values of the module / (Diametral Pitch with a calculation in imperial units) and in case of a selection from this list, the chosen value is added to the field on the left automatically.
Design of correct dimensions of the module is quite a complex task. Therefore, it is recommended to use a procedure for the design of toothing based on the ratio of the width of the pinion to its diameter [4.5].
Width of toothing b of individual gears is measured on a pitch cylinder. Width of toothing of the pinion is usually greater than the width of the gear by the size of one module.
These values depend on the chosen material and the type of gearing [2.1,2.2,2.5]. The recommended range of values is given in the previous row.
This is a common width of both gears on rolling cylinders. If the gears are not in offset positions (Fig. 4.1), it is mostly the width of the gear. This width is used for strength checks of toothing.
In case the check box in this row is enabled, the "Working width of toothing" is filled out automatically with the lower value of the width of toothing from the previous row [4.9]
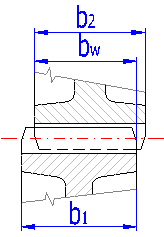
This parameter gives the ratio between the entered width of the pinion and its calculated pitch diameter. The maximum value is given in the green field on the right.
This is calculated as the weight of full cylinders (without weight removal and holes). It serves for quick orientation during the design. In paragraph [8.0], it is possible to refine the calculation of weight.
The row always gives the lower of the coefficients for the pinion and the gear. The first column contains the coefficient of safety for the contact fatigue; the second column then contains
This is the perpendicular (shortest) distance between non-working sides of teeth. A backlash is necessary to create a continuous layer of lubricant on sides of teeth and to overcome production inaccuracies, deformations and thermal expansion of individual elements of the mechanism. Very small clearances are required in gearing of control systems and instruments and if it is not possible to eliminate it, gearing with automatic take up of backlash is usually used. Great backlash must be chosen with heavily loaded gearing (thermal expansion) and high-speed gearing (hydraulic resistance and shocks with pushing of oil off the inter-tooth gaps.
In practice, the recommended values are chosen empirically and you can follow the recommended values in row [4.16].
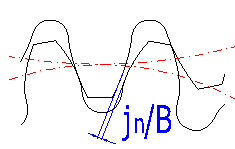
After entering the backlash, the working axis distance [6.10] is modified so that the entered backlash is created. On the other hand, in the course of calculation of toothing for an exact axis distance [14] the toothing is corrected [5.6] so that the entered backlash is achieved.
Option of coefficients of shifts x1 and x2 is the basic task when designing gearing, above all, in case of gears with straight teeth. The shift affects geometric and kinematic and strength characteristics as well. When designing corrections, first it is necessary to fulfill functional requirements and then optimize the corrections to improve some of the other parameters of the gearing.
Approaching and withdrawal of the production tool from the gear center changes the shapes and therefore also properties of the involute toothing. This creates corrected toothing. The illustration shows:
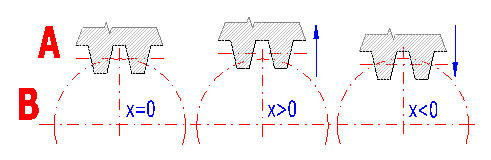
Correction of toothing enables:
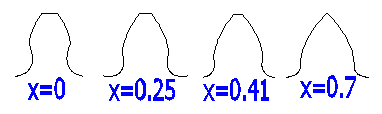
Example of a tooth profile (z=10, a=20;
When determining values of corrections, first it is necessary to fulfill functional requirements for toothing, where the most important items include
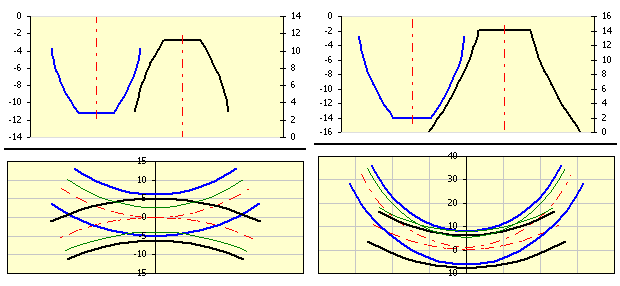
After securing function requirements, it is possible to further optimize corrections in order to improve one or more important toothing parameters. From the frequently used optimizing methods, it is possible to optimize the toothing in order to balance specific slips [5.10, 5.11] and minimize specific slips [5.12]. For other optimizing processes there is a wide range of recommendations in professional literature, namely the so-called diagrams (charts) of limit corrections, providing a clear view of possibilities and selection of corrections.
Example of tables of maximum values of corrections for the coefficient

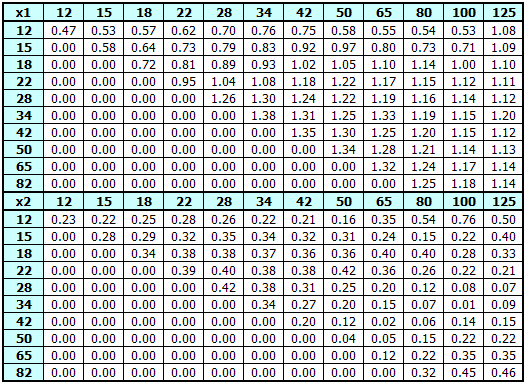
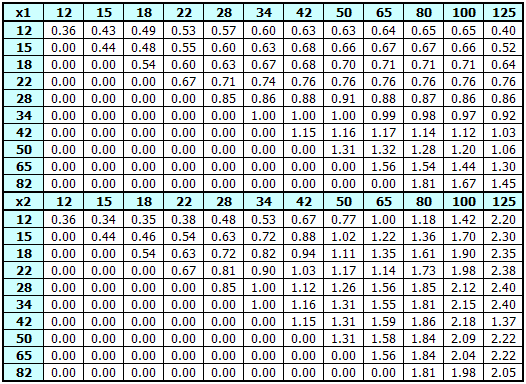
The left illustration shows important diameters of the pinion and gear in the mesh, where:
The illustration on the right shows shapes of the pinion (blue) and the tooth (black).
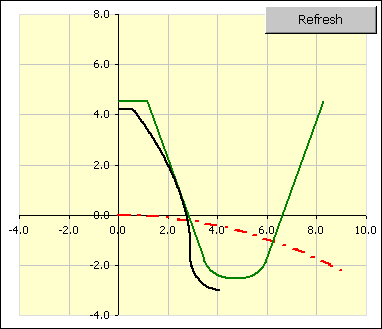
In the picture of the shape of tooth and tool, you can check tooth shape and tool bite visually. The accurate tooth shape is black, while the accurate shape of machining tool is green. You can switch between the picture of pinion tooth and wheel tooth and set the orientation of the tool in bite in line [5.15].
This is the minimum value of a correction which can be used without admissible (minor, tolerable) undercutting of teeth.
This is the minimum value of a correction which can be used without undercutting of teeth.
This is the minimum value of a correction which can be used without tapering of teeth.
This slider is designed to quickly change distribution of corrections. In case the check box to the right of the slider is enabled, slider movements control distribution of the sum of corrections [5.6] to individual gears. It is advisable to use this function at the moment when you wish to optimize some of the qualitative or strength parameters of the gear, the most important of which are given in rows [5.8-5.14].
Here the distribution of the total correction to the pinion and gear is given. In case you wish to enter addendum modification coefficients of the pinion using the keyboard, disable the checkbox in row [5.5].
The column on the left includes the input field for entering sums of addendum modification coefficients; this field is subdivided into individual gears. The right column includes the minimum value resulting from the condition of the limit pressure angle. (The sum of addendum modification coefficients must always be higher).
After a change in corrections, it is advisable to watch the behavior of these indices. Exceeding critical values is indicated by a change in the number.
Detailed description [8.1] a [8.2]
This is a dimensionless parameter (proportion of the tooth thickness and the module) and depends, above all, on the tooth shape. The following parameters also have certain effects:
Usually it is 0.25 - 0.4. Higher for low values of the addendum modification coefficients and hardened gears. A smaller value than the recommended is indicated by a red text, exceeding the limit of tooth sharpness by a red field.
One of the most frequent optimizing tasks applies to finding such corrections x1 and x2 in order to balance specific slips on hubs / bases of wheel and pinion. The principle is described in professional literature. This calculation specifies the value of specific slip on the base (hub) of pinion (wheel) in lines [5.10] and [5.11]. By sliding the slider in line [5.5] and changing the value of correction x1 and x2 that way, you can easily find the values of corrections in order to achieve approximately the same values of specific slips in lines [5.10] and [5.11].
This optimization method is applicable for the wheels with approximately the same number of teeth and manufactured from the same material. If the number of teeth varies, the pinion teeth engage more frequently than the wheel teeth and in the case of balanced specific slips the base of the pinion tends to pitting.
Therefore the correction in order to achieve minimum sum of absolute values of all specific slips may then be more appropriate than the correction in order to balance specific slips [5.10, 5.11]. In such case it is also advantageous that the transmission efficiency increases (losses due to friction are reduced).
Detailed information [10].
In this line, choose whether a detailed profile of the pinion or wheel tooth shall be displayed and use the slider to set orientation of the tool in bite.
This paragraph includes a well-arranged listing of all basic dimensional parameters of toothing. An informational illustration of the most important dimensional parameters is given here. It is recommended to use specialized literature for a more detailed description of individual parameters.
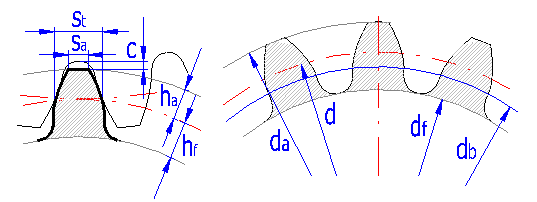
Specification of dimensions according to ISO (DIN)
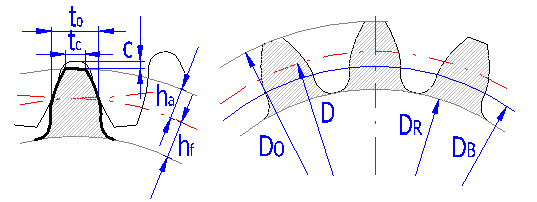
Specification of dimensions according to ANSI (AGMA)
This is a dimensionless parameter (proportion of the tooth thickness and the
module) and depends, above all, on the tooth shape. The following parameters
also have certain effects:
- higher number of teeth [4.1] = greater sa*
- lower addendum modification coefficient [5.4] = greater sa*
- smaller meshing angle [4.2] = greater sa*
- greater helix angle [4.3] = greater sa*
- higher addendum coefficient [3.1]= smaller sa*
Recommended values
Usually it is 0.25 - 0.4. Higher for low values of the addendum modification
coefficients and hardened gears. A smaller value than the recommended is
indicated by a red text, exceeding the limit of tooth sharpness by a red field.
In practice, it is sometimes achieve certain exact values of the head circle. If the original gearing dimensions should be maintained, it is possible to slightly change the head circle diameter by changing the tooth tip backlash ca* in the section [3.11]. The following three lines are used to simplify this calculation. On the second line, the possible range of the head circle diameters are mentioned. Enter the required diameter on the third line. Press the "->ca1" ("->ca2") button to change the tooth tip backlash of the pinion (wheel).
This paragraph includes the minimum numbers of teeth which can be used with zero correction without undercutting or tapering of teeth.
This includes the parameters which inform us of the quality of the designed toothing. It is advisable to compare them with the recommended values.
For smooth meshing of gears, it is necessary that the other pair of teeth enters in meshing before the first pair is released. The contact ratio in the face plane says how many teeth are in meshing simultaneously. With the value ea=1 this corresponds to a limit case when only one pair of teeth is in meshing at the given moment. With the value
According to the complexity of the gearing, this parameter should not be lower than 1.1 to 1.2.
This is the sum of transverse contact and overlap ratios.
This is specified using the same recommendations as
Lines [8.7 - 8.10] enable more precise specification of the dimensions of individual wheels. After checking the box on the line [8.7], you can specify relevant dimensions according to the headline of this section. Press the "<=" button [8.7] to fill in the pre-selected values.
The shape of individual wheels is displayed acc. To the specification. If no inner wheel dimensions are specified, the wheels are considered as solid cylinders in the calculation.
Using the "Automatic design " [2.10], gearing design [4.4] and the exact mn calculation [4.6] will cancel the wheel specification and the solid cylinders will be used instead.
It is estimated based on the transferred power, way of loading and the pinion material. This is used only for reference when designing the wheel dimensions.
A reference value derived from the minimum diameter of the shaft.
This parameter gives the ratio between the root diameter and the inner diameter of the toothed rim di/df (Pic. 8.3). It is characterized with values in a range from 0 to 100%. In case the evaluated gear will be produced as a solid disc (without weight reduction), the parameter = 0. This parameter affects calculations of critical speed of the gearing.
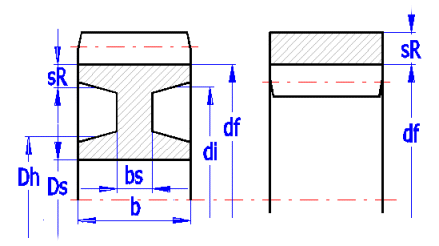
It is calculated as a sum of individual cylindrical parts (ring gear, stem and hub). If the relief coefficient di/df = 0, the wheel weight is calculated as the weight of the solid cylinder (which is sufficient in most cases). This is used for a quick reference in the design.
This is another important qualitative parameter which affects the desired accuracy of the gearing [2.6] and the manner of lubrication (Lubrication of gears).
This is the speed at which the angle speed is the same as the proper angle vibration frequency of the gearing.
This is the ratio of pinion speed and "Critical speed".
In case the designed gearing works in the range of critical speed (N ~ 1), the resonance ratio N is indicated by a red number. In such cases, modifications of the designed gearing (changes of numbers of teeth) or consultations with a specialist are recommended.
Exact determination of the loss coefficient is very difficult. Therefore, the approximate calculation based on the number of teeth, contact ratio, angle beta and coefficient of friction is used here. The choice of the coefficient of friction is based on the chosen degree of accuracy of the toothing [2.6], in a range from 0.04 to 0.08
The calculation of coefficients / factors in compliance with ISO6336:2006 or AGMA 2001-D04, AGMA 908-B89/95. The details are described in the theoretical part; the list of standards and literature used are mentioned at the end of this help.
In this part, the calculation method of some coefficient should be specified. After pressing the button, the default values are set based on the requirements mentioned in the paragraph [2.0]
There are three calculation methods available - (B2006), (C2006), and (C1996).
The method B is suitable for all the types of spur gears. It is relatively complicated and may give completely unrealistic KV values, if the materials or the degree of accuracy are not properly selected. Therefore it is possible to set the maximum limit for the calculation (pre-set to 5.0). If this limit is exceeded, it is recommended to check the selected material and the degree of accuracy in proportion to the gearing load. The method C may be used with some limitations (see the theoretical part).
There are three calculation methods of
It depends on a range of factors, firstly on the specific dimensions and the
design of the gearing (see the theoretical part). It is possible to set all
these parameters in details in the paragraph [18.0]. If the input parameters are
not selected properly, the
Press the "=>" button to move to the
According to the ISO 6336-5 standard, it is recommended to reduce the value
By selecting "Automatic" one can choose a coefficient calculation method based on the selected materials. If required, you can select the calculation method directly from the list.
If you select an optimum modification of the tooth profile with respect to
the tooth deflection due to an immediate load level, select "Optimum profile
modification". Selection of this parameter influences the calculation method of
the coefficients
Use the drop-down menu to choose the type of oil. For less stressed gearings, you can use mineral oil; for higher speeds, higher transmitted power and higher efficiency requirements, it is more appropriate to use synthetic oil.
Some advantages of synthetic oils
- Reduction of total losses of 30% and more
- Reduction in oil working temperature
- Increasing the interval for oil replacement by 3-5x (reduction in maintenance
costs)
On the other hand, the price is higher, there may be problems with plastic or rubber parts, and the mixing with mineral oil is limited.
The recommended viscosity is chosen based on the hardness of the wheel material and the circumferential velocity. If the recommended value is not suitable, check the radio button and enter your own value.
If the first item in the "Automatic" list is selected, the applied surface roughness will be derived from the selected degree of accuracy. However, a different value may be set, if it is known.
It considers a higher capacity for a limited number of load cycles. The coefficient is derived from interpolations of relevant damage line (ISO6336, AGMA 2001-D04). For the number of cycles N = 1010 (marked as ∞), the coefficient value is selected in the range of 0.85 to 1.00. The value of 0.85 is intended for the critical operation whereas the value of 1.00 may be used when the optimum lubrication, material, production and experience are ensured.
The toothed wheel notch (e.g. ground notch in the tooth root transition near the critical cross-section) usually increase the stress concentration caused by the root transition; therefore the stress concentration coefficient is higher accordingly. If the notch is located near the critical cross-section, the coefficient YSg is used instead of YS.
If the radio button is checked, the YS value is substituted by the YSg value. The YSg coefficient values are calculated in the paragraph [18.0] that can be accessed by pressing the "=>" button.
In this section, the calculation method of certain coefficients should be specified. When pressing the button, the default values are set based on the requirements in the paragraph [2.0].
In compliance with ANSI/AGMA 2001-D04 it is recommended to reduce the value
According to AGMA 2001-D04, YN=0.9 and ZN=0.85 is selected for the number of cycles N=1010 and for a normal use. Use the values of YN=0.8 and ZN=0.68 for the critical applications.
This paragraph contains all the stress values (bend, contact) necessary for the safety coefficient calculations.
Two basic strength calculations are usually carried out, namely for bend and for contact. The following safety coefficients are calculated in this calculation:
As initial values of the safety coefficient you can use:
Safety coefficients can then be modified according to general recommendations for options of safety coefficients and according to your own experience.
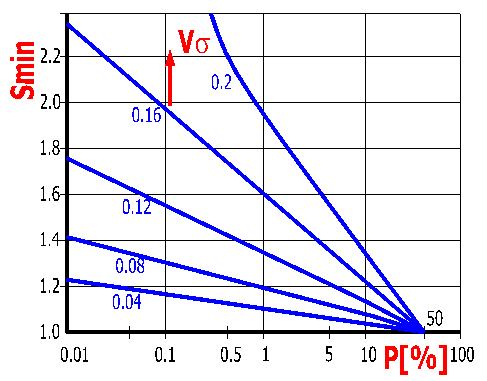
This is calculated additionally after pressing the button "Calc". This parameter gives the probability of a failure in the gearing. It is based on the diagram (see the illustration). Probability of a failure is a function of the level of safety Smin [10.1, 10.2] and the variability coefficient Vs [10.5].
In case of common gearing, the calculation probability of a failure should be about 1%, in case of important gearing, the value should be under 0.1 to 0.01% (even less for very important gearing).
This paragraph contains the toothing check dimensions, correction setting to obtain these dimensions, and tolerances in accordance with ISO 1328 / ANSI/AGMA 2015-1-A01, 2015-2-A06.
This paragraph specifies two basic check dimensions
of toothing. They are the dimension across the teeth W [11.4] and dimension
across the rolls and balls M [11.7]. After checking the check box to the right
of the value of number of teeth that the measurement applies to [11.3] and the
diameter of roll/ball [11.6] you can set your own values. Other check dimensions
required for production of toothing are tied to fitting of toothed wheels and
manufacturing method and therefore close cooperation of a designer and a
technologist is appropriate.

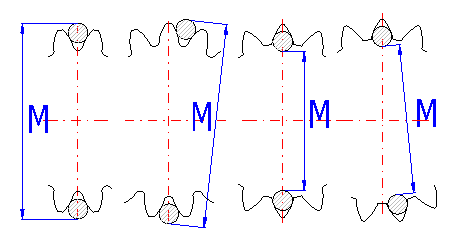
If you try to find the parameters of an unknown wheel, it is possible to use this tool. Measure the relevant check dimension on the wheel, enter it in the respective input field and the calculation will modify the correction x1 (SumX) so that the calculated W or M dimension agrees with the measured value.
This part contains a complete calculation of tolerances in accordance with ISO 1328 (ANSI/AGMA 2015-1-A01). The tolerance calculation is linked with the main calculation and the tolerances are calculated for a current accuracy, module, diameters and the width of the wheels. The tolerances are then used for the safety coefficient calculations.
If you need to calculate the tolerances for different toothing diameters independent on the actual calculation, check the radio button on the line [11.14]. The colour of the input boxes [11.15, 11.16, and 11.17] will change to white and you can enter your own values of the toothing dimensions.
Accuracy grades A2 through A11
0.5 ≤ mn ≤ 50
5 ≤ z ≤ 1000 or 10000/mn whichever is less
5 ≤ dT ≤ 10000 mm
f'isT, F'isT: 5 ≤ dT ≤ 2500 mm
FbT: 5 ≤ dT ≤ 4000 mm; 4 ≤ b ≤ 1000 mm
Accuracy grades C4 through C12
0.2 ≤ mn ≤ 5
2 ≤ d ≤ 1000 mm
3 ≤ z ≤ 1000
β ≤ 45°
FrT: 0.5 ≤ mn ≤ 50; 5 ≤ d ≤ 12000 mm
Possible ranges of imputs for f''I
and F''i:
Accuracy grade Q: 4-12
Modul mn: 0.2-10
Diameter d: 5-1000
Facewidth b: 4-1000
Loaded gearing creates forces which are transferred to the machine structure.
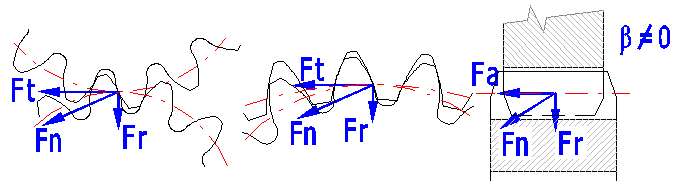
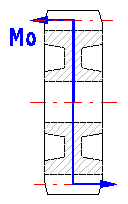
Helical gearing creates an additional bending moment which must be taken into account when designing the shaft.
This is another important qualitative parameter which affects the desired accuracy of the gearing [2.6] and the manner of lubrication (Lubrication of gears).
This is another qualitative index which is used for calculation of the "Coefficient of fluctuations in loading of the teeth".
In most cases, the axis distance of the pinion and the gear is not a result of calculation of the toothing, but is one of the input parameters which must be followed. The axis distance is often chosen in a standardized series. The desired axis distance can also be achieved in two ways, namely by:
| ID | Serial number |
| z1/ |
Number of teeth of the pinion |
| z2/N2 | Number of teeth of the gear |
| i | Transmission ratio |
| b | Helix angle |
| S x | Sum of addendum modification coefficients |
In this case, the axial distance influences only setting of a pinion addendum modification coefficient (x2 = 0 for the rack). The current axial distance aw and the axial distance range that may be obtained by changing x1 are mentioned on the line [14.1].
Set the axial distance on the line [14.2]. Press the button "->x1" to change the addendum modification coefficient of the pinion.
This paragraph enables an orientation calculation of the lost heat and gearbox surface necessary for dissipation of this heat.
Temperature of the oil in the gearbox should be in a range from 50 to 80 °C; a lower temperature should be found in smaller modules. More exact determination of temperature depends on the chosen construction and used materials. Higher temperatures bring a danger of lower backlash and the gearing could seize.
This depends on the construction and ambient environment of the gearbox. Initially, it is possible to choose:
for ISO:
for ANSI:
This depends on the total transferred power and efficiency of the gearing.
This parameter gives the minimum surface of the gearbox necessary for dissipation of power losses and maintaining the desired oil temperature.
This paragraph gives designs of shaft diameters (steel) which correspond to the desired loading (transferred power, speed). These values are orientation values only; it is advisable to use a more exact calculation for the final design.
In practice, you face quite frequently a situation where the toothing is unknown and it is necessary to calculate its parameters (competition comparison, production of a spare gear, etc.). Therefore, this provides a simple tool to facilitate the primary calculation of the basic parameter - module.
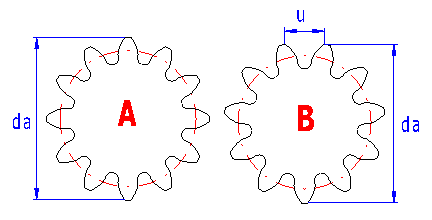
It is obvious that the mentioned procedure needs certain skills and experience, nevertheless, in case of common gearing, where production using common standardized tools and procedures can be assumed, this procedure leads to quite reasonable results.
Auxiliary calculations are available in this paragraph. When entering values, use the same units as in the main calculation. To transfer the entered and calculated values to the main calculation, press the button "OK".
The KHb and YSg calculation is described below.
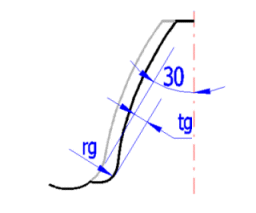
The KHb calculation consists of the sequence of several steps
1) Calculation of fsh = f(Fm, dsh, K',
l, s, b1,
d1)
2) Calculation of fma = f(fHb1
, fHb2)
... [11.29]
The fsh and fma values (or fsh2, fca, fbe) are used to calculate the value of Fbx
3) Calculation of Fbx
= f(fsh, fma, fsh2, fca, fbe, B1, B2)
4) Calculation of yb
= f(Fbx, sHlim)
5) Calculation of Fby
= f(Fbx,
yb)
6) Calculation of KHb = f(Fby,
Fm,
cgb,
b)
The range of coefficients may be specified using several methods and the designed / checked gearing must be well understood. Press "Default setting" for the basic design. By doing this, the calculation will be set to the basic conditions as follows.
- [18.8] ... set according to the selection of [2.5]
- [18.9, 18.10] ... dimensions estimated from the gearing size and setting of
[18.8]
- [18.16, 18.17] ... set according to the selected degree of accuracy [2.6]
Then you can gradually enter and set up the parameter that are known or can be estimated.
You can enter your own values after checking the check box next to the relevant input.
It is a pre-selected value based on the root diameter of the pinion and the minimum shaft diameter [8.4]. If you know the shaft diameter, check the radio button and enter your own value.
Select the type of gearing.
Select a relevant pinion mounting from the list, see the picture. Pre-set according to [2.5].
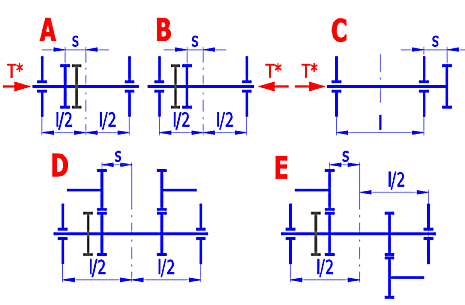
The "l" and "s" values are preliminarily derived from the wheel width and from the selected mounting of the gearing [18.8]. After checking the radio button, you can enter your own values.
The values of fsh, fsh2, fma, fca, and fbe describe deformations of the toothed wheels, wheel tolerances, and mounting tolerances. The values of fsh2, fca and fbe are not considered in this calculation and they can be zero unless you solve a complete equation to calculate Fbx [18.17]. The values of fsh and fma may be directly entered, or the values calculated based on the parameters on the previous lines may be used.
Select the apropriate modification of the tooth slope from the list. See ISO6336:1(2006) for more details.
Select the Fbx calculation from the list.
1. Proper value
2. Gear pairs of which the size and suitability of the contact pattern are not
proven and the bearing pattern under load is imperfect
3. Gear pairs with verification of the favourable position of the contact
pattern (e.g. by modification of the teeth or adjustment of bearings)
4. When, apart from pinion body and pinion shaft deformations, those of the
wheel / wheel shaft and the gear case and also the displacements of the
bearings.
Press "OK" button to return back to the paragraph [9.0]. At the same time, the KHb calculation is set up in the calculation of the coefficients in accordance with ISO6336.
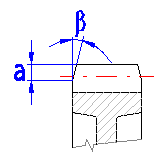
The toothed wheel notch (e.g. ground notch in the tooth root transition near the critical cross-section) usually increase the stress concentration caused by the root transition; therefore the stress concentration coefficient is higher accordingly. If the notch is located near the critical cross-section, the coefficient YSg is used instead of YS.
Fill in the notch parameters, see the picture. By pressing the "OK" button, you return to the paragraph [9.0] and the YS coefficient is substituted by YSg.
The material type for which you want to determine the material properties can be selected from the list.
The relations used are specified for three levels of the material quality - ML, MQ and ME.
- ML represents the weakest material quality and its heat treatment process
requirements during the toothed wheel manufacturing.
- MQ represents requirements that may be satisfied by a skilled manufacturer
with reasonable production costs.
- ME represents requirements that must be satisfied to achieve a high
operational reliability.
(See the description in the standard for the AGMA grades 1-3.)
Enter the surface hardness. The material parameters are determined by its type and hardness. At the end of the line you can find the hardness range for which the parameter calculations are applicable. The hardness may be entered in various units (HV, HB and HRC).
If you enter your own material values and you will add the material in the table of materials, select the correct marking heat treatment method acc. To ANSI/AGMA). This marking will be used to choose some of the coefficients in the strength calculation.
If the radio button on the line [19.5] is checked, it is possible to enter the own material description that will be mentioned in the table of materials and will be used for the material selection in the paragraph [2.0].
Select one of the 5 lines intended for the user defined materials from the list. When the values are transferred, the original content in the table of materials will be overwritten without any caution.
Use the following table for your decision on the manner of lubrication of the gearing.
| Type of lubrication | Peripheral speed in | |
| [m/s] | [ft/min] | |
| Oil-bath lubrication | < 12 | < 2400 |
| Pressure spray lubrication | > 12 | > 2400 |
| Oil-mist lubrication | > 60 | > 12000 |
Information on options of 2D and 3D graphic outputs and information on cooperation with 2D and 3D CAD systems can be found in the document "Graphic output, CAD systems".
1. In the "Output of a 2D drawing into" list, choose the target CAD system (target application) to which the picture should be generated, or a "DXF File" to convert the drawing into a .DXF file.
2. In the "Scale of 2D drawing" list, set up the drawing scale. The drawing is always created in the scale 1:1. The scale allows you to set only certain parameters of the drawing, such as the size of the text or overlapping of the axes.
3. If necessary, set up another control elements as well. Most calculations also include other setting options, which depend on the calculation and type of the plotted object. Explanation of these supplementary options can be found in the help for the respective calculation.
4. Start plotting using the button with the icon of the desired drawing.
The angle sets rotation of the drawing of the gearing by the defined angle from the horizontal axis (illustration - see the button).
These parameters set beveling of the gear according to the illustration.
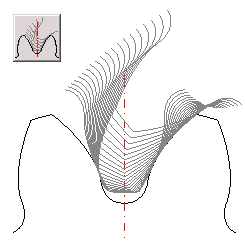
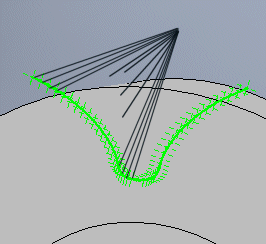
Besides standard display which is used in drawings of assemblies and details, it is also possible to draw a detailed image of the tooth, detail of entire wheel, drawing of wheel engagement and drawing of the tool. Tooth flank is calculated from the simulation of the tool bite with the machined wheel which enables determining the exact tooth shape including the tooth flank. A detailed drawing of the whole wheel can be used as a document for manufacturing an accurate model in 3D CAD system, or as input data for manufacturing the wheel.
The table on sheet "Coordinates" gives the coordinates of points on the right side of the tooth line (both pinion and wheel) in the system of X,Y coordinates with point 0,0 in the wheel centre. In order to recalculate and generate the current coordinates according to the settings from paragraph [20] press button "Refresh".
Production tool (B) with dimensions defined in paragraph [3] is gradually rolled away along the circle (C) with step of angle W and thus creates the tooth line (A) in individual points (2).
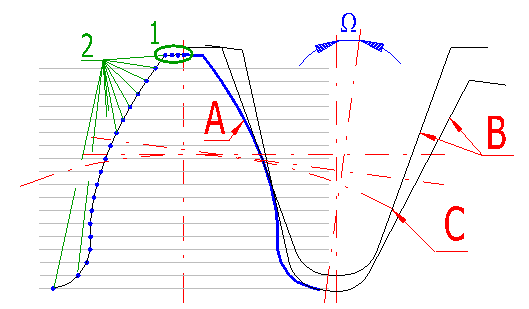
Specify the number of teeth which shall be drawn in partial drafting. Pinion teeth are drawn in upward direction, wheel teeth in downward direction, always symmetrically along the vertical axis. In the picture, 3 teeth are set for the pinion (lower wheel) and 4 teeth for the wheel.
Define the number of points (sections) on the tooth tip, see picture [20.4],
reference (1).
Range of permitted values: <2 - 50>, recommended: 5
Define the number of points (sections) which form a complete tooth flank, see
picture [20.4], reference (2).
Range of permitted values: <10 - 500>, recommended: 30 and more
It defines the increment of angle for rolling (turning) of the tool during
machining of the tooth flank see picture [20.4], angle W.
Extent of permitted values: <0.02 - 10>, recommended: 0.5
Defines how many positions during the drawing of tooth engagement will be
displayed.
Extent of permitted values: <3 - 100>, recommended: 20
As it is necessary and appropriate to check tooth engagement as well as potential collisions of teeth for internal toothing, the drawing of complete engagement of outer as well as inner gear is generated for internal toothing. In this case, number of copies of teeth during the check of engagement [20.9] specifies number of pinion copies.

Gives turning of the pinion between individual copies of the pinion which are generated during the check of engagement.
Switch "Drawing without axes" defines if the axes will be removed in the inserted drawing.
Example of 3D model


Locate the text description in the 2D drawing by pressing the button “Draw”.
The text can be edited after the tick off box has been activated.
If it is supported by the respective module for entering models into a 3D CAD
system, the contents of individual rows is entered into user attributes of the
model and these can be used when generating a BOM.
(Details can be found in Help for connection to the respective 3D CAD system.)
A series of calculations (gearing, springs, etc.) enables entering of the respective table with text information on the calculated object into the drawing. The table can be selected from the respective list (in case the calculation enables more types to be entered). Drawing of the table can be activated by pressing the button “Draw a table”.
The option to generate the profile of the gear wheel as a sequence of line sections (DXF) is expanded with the option to generate the directrices, which define the sides of the tooth and thus allow creation of the smooth (extrapolated) curve in the corresponding CAD system. This allows the creation of non-parametric but precision 3D models of the gearing.
General procedure:

For the majority of spur gearings, it is sufficient to have a contact angle that is identical for the engaging and non-engaging sides. However, it may be suitable to select a different contact angle for some applications. After ticking the button on the right, you can enter different contact angles for each side of the tooth.
It states how many points will be generated to define the tooth side curve. Normally, the suitable value is 20. For special cases (limitations of the CAD system, precision, etc.) it is possible to use values 12 to 200.
Above the generated profile of the gap between the teeth, another piece is added, which can be suitable for better selection of the curves, or whose presence is necessary to correctly interpret the curves.
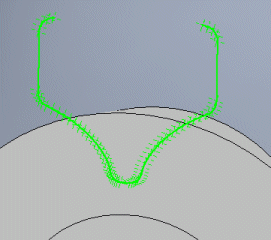
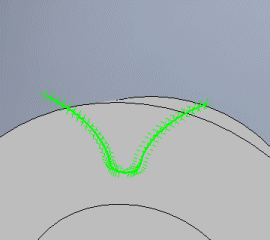
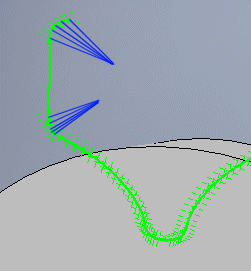
It states the number of points to be used for the curvature of the connection and end of the superstructure. In most cases, five is sufficient.
Some CAD systems require a closed profile, while some require a profile that is manually opened or closed. The switch connects/disconnects the first and last points of the profile.

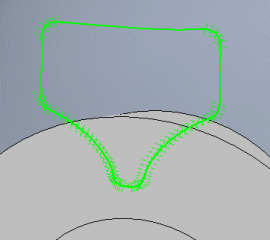
Various CAD systems support importing points that form the curves in various formats. The following formats are available:
It inserts a small circle into each point of the curve. Suitable in a case where the CAD system is capable of downloading only the DXF format and it is necessary to create a profile manually, point by point.
The height of the imaginary cylinder (pitch diameter) on which one rotation is accomplished. Mostly, this data item must be entered for rotation with extension in 3D CAD.
The parameters of the gearing that fully define the geometry and important dimensions are entered in short form in the line.
Information on setting of calculation parameters and setting of the language can be found in the document "Setting calculations, change the language".
General information on how to modify and extend calculation workbooks is mentioned in the document "Workbook (calculation) modifications".
Material list - Method of heat treatment
1...Non-treated thermally, annealed normalizationally
2...Upgraded
3...Cemented, hardened, surface hardened
4...Nitrided
ISO 6336-1:2006
- Calculation of load capacity of spur and helical gears - Part 1: Basic
principles, introduction and general influence factors
- Calcul de la capacité de charge des engrenages cylindriques a dentures droite
et hélicoidale - Partie 1: Principles de base, introduction et facteurs généraux
d'influence
- Výpočet únosnosti čelních ozubenych kol s přímými a šikmými zuby - Část 1:
Základní principy, doporučení a obecné ovlivfňující faktory
ISO 6336-2:2006
- Calculation of load capacity of spur and helical gears - Part 2: Calculation
of surface durability (pitting)
- Calcul de Ia capacité de charge des engrenages cylindriques à dentures droite
et hélicoidale - Partie 2: Calcul de la résistance à la pression de contact (piqure)
- Výpočet únosnosti čelních ozubených kol s přímými a šikmými zuby - Část 2:
Výpočet trvanlivosti povrchu (pitting)
ISO 6336-3:2006
- Calculation of load capacity of spur and helical gears - Part 3:
Calculation of tooth bending strength
- Calcul de la capacité de charge des engrenages cylindriques à dentures droite
et hélicoïdale - Partie 3: Calcul de la résistance à la flexion en pied de dent
- Výpočet únosnosti čelních ozubených kol s přímými a šikmými zuby - Část 3:
Výpočet pevnosti v ohybu zubu
ISO 6336-5:2003
- Calculation of load capacity of spur and helical gears – Part 5: Strength and
quality of materials
- Calcul de la capacité de charge des engrenages cylindriques à dentures droite
et hélicoïdale – Partie 5: Résistance et qualité des matériaux
- Výpočet únosnosti čelních ozubených kol s přímými a šikmými zuby – Část 5:
Údaje o pevnosti a kvalitě materiálů
ISO 1265
- Metalic materials - Conversion of hardness values
- Matériaux métalliques - Conversion des valeurs de dureté
- Metallische Werkstoffe - Umwertung von Hartewerten
- Kovové materiály - Převod hodnot tvrdosti
ISO 1328-1:1997
- Cylindrical gears - ISO system of accuracy - Part 1: Definitions and allowable
values of deviations relevant to corresponding flanks of gear teeth
- Engrenages cylindriques - Systéme ISO de precision - Partie 1: Définions et
valeurs admissibles des écarts pour les flanc homologues de la denture
- Toleranzensystem ISO - Teil 1: Toleranzen fur Flankenlinienabweichungen
- Čelní ozubená kola - Soustava přesnosti ISO - Část 1: Definice a mezní úchylky
vztažené na stejnolehlé boky zubů ozubeného kola.
ISO 1328-2:1997
- Cylindrical gears - ISO system of accuracy Part 2: Definitions and
allowable values of deviations relevant to radial composite deviations and
runout information
- Engrenages cyindriques - Systéme ISO de precision Partie 2: Definitions et
valeurs admissibles des ecarts composés radiaux et information sur le faux-rond
- Čelní ozubená kola - Soustava přesnosti ISO - Část 2: Definice a hodnoty
dovolenych úchylek relevantní k radiálním kinematickým úchylkám a informativně k
obvodovému házení.
ISO 1122-1:1998
- Vocabulary of gear terms - Part 1: Definitions related to geometry
- Vocabulaire des engrenages - Partie 1: Définitions géométriques
- Slovník termínů ozubení - Část 1: Definice vztahující se ke geometrii
ANSI/AGMA 2001-D04
AMERICAN NATIONAL STANDARD Fundamental Rating Factors and Calculation Methods
for Involute Spur and Helical Gear Teeth
AGMA 908-B89
Geometry Factors for Determining the Pitting Resistance and Bending Strength of
Spur, Helical and Herringbone Gear Teeth
ANSI/AGMA 2015- 1-A01
Accuracy Classification System - Tangential Measurements for Cylindrical Gears
ANSI/AGMA 2015-2-A06
Accuracy Classification System - Radial Measurements for Cylindrical Gears