Die Berechnung ist für den Entwurf der Geometrie und der Festigkeit und zur Kontrolle der Schneckenräder bestimmt. Das Programm löst folgende Aufgaben.
Die Berechnungen verwenden Verfahren, Algorithmen und Angaben aus Normen ANSI, ISO, DIN, BS und aus der Fachliteratur.
Normenverzeichnis: ANSI/AGMA 6022-C93 (Revision of AGMA 341.02), ANSI/AGMA 6034-B92 (Revision of ANSI/AGMA 6034-A87), DIN 3996, DIN 3975-1, DIN 3975-2
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Die Schneckenräder (globoid) können große Leistungen übertragen, üblich 50 bis 100 kW (optimal 0.04kW-120kW, extrem 1000 kW); sie sind in der Lage, in einer Stufe hohe Übersetzungsverhältnisse i = 5 bis 100 zu realisieren, (bei kinematischen Übersetzungen bis i=1000). Sie haben dabei kleine Maße, ein niedriges Gewicht und sind in der Bauweise in sich abgeschlossenen (kompakt). Sie zeichnen sich durch einen ruhigen und leisen Lauf aus und können als eine selbsthemmende Übersetzung entworfen werden.
Ungünstig ist ein großer Schlupf in der Verzahnung, der eine größere Verlustleistung durch Reibung verursacht, und dadurch auch ein niedrigeres Wirkungsgrad der Übersetzung; das Bestreben um eine Verbesserung zwingt zum Einsatz von mangelnden Nichteisenmetallen für die Schneckenräderkränze. Die Herstellung einer Verzahnung ist anspruchsvoller und teuerer und ihre Lebensdauer ist wegen des Verschleißes niedriger als die bei den Wälzrädern.
Sie werden als Leistungsübersetzungen eingesetzt - für Mischmaschinen, Karusselldrehmaschinen, Fahrzeuge und Hebezeuge, Textilmaschinen, Pressen, Fördereinrichtungen, Scheren, Trommeln, Aufzüge, Schiffsschraubenantriebe, Hobelmaschinen, Werkzeugmaschinen, Kraftfahrzeuge...
In dieser Berechnung werden die am meisten benutzten Räder mit einer Zylinderschnecke und einem Globoidrad gelöst.
Die Schneckenräder sind ein Sonderfall der Schraubenradgetriebe mit einem Achsenwinkel von 90° und mit einer niedrigen Zahnanzahl am Ritzel/Schnecke (meistens von z1=1-4). Es wird dabei je nach der Form unterschieden:
ZA - spiralförmig, mit einem geradlinigen (trapezförmigen) Zahnprofil im Achsenschnitt, im Normalschnitt sind die Zahnflanken leicht konvexförmig, ein Querschnitt führt zur Archimedes-Spirale. Es werden meistens Elemente im Achsschnitt normalisiert, d.h. mx=m, ax=a. Die Verzahnung wird auf einer Drehbank oder auf Gewindeschneidmaschinen gefertigt (die Schnecke erinnert an eine Bewegungsschraube mit Gewinde trapezförmigen Profils). Das Messer mit dem Grundprofil wird zum Werkstück in der Achsenebene angelegt. Bei größeren Winkeln g entstehen beim Formmesser an den Seitenschneiden abweichende Schnittwinkel, was zu einer ungleichen Beanspruchung und Abstumpfung der Schneiden führt. Die Seitenflächen der Schnecke können nur unter dem Einsatz einer speziellen Schleifscheibe geschliffen werden. Bei Schnecken mit einem kleinen Steigungswinkel (g<10°) wird deshalb die spiralförmige Verzahnung verwendet und zwar in Fällen, wenn die Zahnflanken nicht thermisch behandelt werden und keinen Nachschliff verlangen
ZN – Schnecke mit einem geradlinigen Profil im normalem Zahnschnitt, und
zwar:
a) Auf der mittleren Schraubenlinie des Spalts
b) Auf der mittleren Schraubenlinie des Zahnes
Im Achsenschnitt sind die Zahnflanken leicht konvexförmig, ein Querschnitt
führt zu einer allgemeinen Evolventenkurve (zur verlängerten oder verkürzten
Evolvente). Es sind Elemente in der Normalebene normalisiert, d.h. mn=m,
an=a.
Die Verzahnung wird gedreht im Falle a) mit einem, im Falle b) mit zwei
Profilmessern in der Normalebene. Die Schnittwinkel sind hier gleich auch bei
großen Winkeln g. Die thermisch behandelten Flanken können mit einer Scheibe mit
geradlinigen Mantellinien auf den Gewindeschleifmaschinen geschliffen werden;
dieses Schleifen führt zu nicht geradlinigen Seitenflächen, welche jedoch sehr
nah den theoretischen Flächen sind. Falls zu diesem Schleifen auch die
Schraubenfräse dienstbar gemacht wird, mit der die Verzahnung des Schneckenrades
gefertigt wird, bilden die Schnecke sowie das Schneckenrad ein theoretisch
richtiges zugeordnetes Paar. Die allgemeine Verzahnung ist auch für Schnecken
mit einem größeren Winkel g und für Schnecken mit thermisch behandelten
Zahnflanken geeignet, die einen Nachschliff benötigen.
ZI – Schnecke mit einem evolventen Profil (ein geradliniges Zahnprofil in der Tangentialebene zum Grundzylinder). Im Achs- sowie auch im Normalschnitt sind die Zahnflanken konvexförmig, der Querschnitt führt zur Evolvente. Die Elemente in der Normalebene sind normalisiert, d.h. mn=m, an=a. Die Verzahnung wird mit zwei an das Werkstück angelegten Profilmessern gedreht. Die Messerschneiden sind in Richtung der Tangentiale zur Schraubenlinie auf dem Grundzylinder gelagert. Die evolvente Verzahnung wird bei Schnecken mit einer größeren Zahnanzahl verwendet, z.B. z1>4; die Schnecke erinnert an ein schrägverzahntes Wälzrad. Die Zahnflanken können mit der flachen Seite der Schleifscheibe geschliffen werden, im Hinblick auf den relativ kleinen g ist es notwendig, spezielle Schleifmaschinen einzusetzen.
ZK – ein durch eine Kegelfläche gebildetes Profil, das mit einem Scheiben-, ggf. mit einem Schaft- werkzeug geschliffen wird;
ZH – ein konkaves Profil der Zähne (das perfekteste und teuerste Profil)
Die für die Berechnung der Geometrie verwendeten Formeln sind in diesem Absatz aufgeführt.
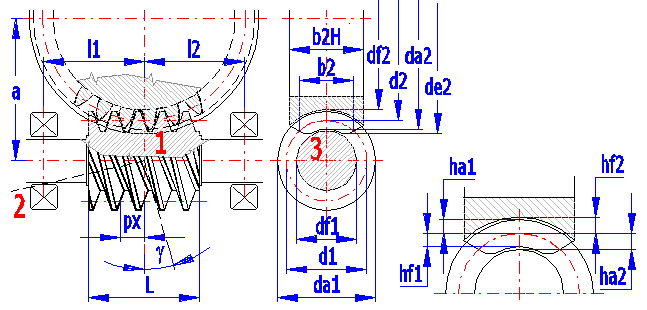
1-Achschnitt (mx,ax,sx,ex) , 2-Normalschnitt (mn,an,sn,en), 3-Stirnschnitt der Schnecke
Parameter des Grundprofils einer Schnecke: m (DP für die Berechnung in Zoll), a,ha*,c*,rf*. Für die Spiralverzahnung ZA werden das Modul und der Eingriffswinkel im Achsschnitt gewählt, für die allgemeinen Verzahnungen ZN,ZI,ZK,ZH werden das Modul und der Eingriffswinkel im Normalschnitt gewählt.
Die Parameter der Schnecke und des Schneckenrades: z1, z2, x1=0, x2=x
ZN: df1=d1 - 2 • (ha* + c*) • mn; df2=d2 - 2 • (ha* + c* - x) • mn
Für die Berechnung der in der Verzahnung entstehenden Kräfte werden folgende Formeln verwendet.
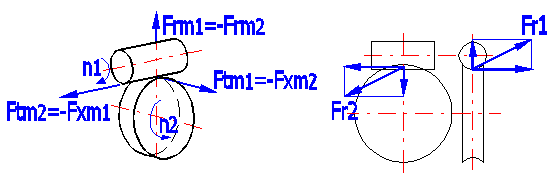
Ftm1=2000 •
T2 / (dm1 •
hges •
z1 / z1) = -Fxm2
Ftm2=2000 •
T2 / dm2 =-Fxm1
Frm1 = -Frm2 = Ftm1
• tan(a)
/ sin(g + r)
Fr1 = (Ftm1^2 + Frm1^2)^0.5
Fr2 = (Ftm2^2 + Frm2^2)^0.5
Die Gesamtverlustleistung im Schneckengetriebe kann auf die Verlustleistungen in der Verzahnung, in den Lagern und Dichtungen unterteilt werden. Die mit einem eventuellen Schmiersystem und einer Kühlung der Übersetzung verbundenen Verluste werden in der Berechnung nicht betrachtet. Das Verzahnungswirkungsgrad ist wie das Verhältnis des antreibenden Glieds und des Antriebsglieds definiert und ist unterschiedlich im Falle, wenn das Antriebsglied die Schnecke (Index 1) und oder das Rad (Index 2) sind.
Der Räderwirkungsgrad hz = tan(g) / tan(g + rz)
wo:
g... Steigungswinkel
r...Reibungswinkel r=atan(m)
Mit wachsendem Steigungswinkel (beim gegebenen Reibungswinkel) steigt der Wirkungsgrad zuerst schnell, geht in eine flache Kurve über und sinkt wieder schnell ab (siehe Abbildung).
Der Kurvengipfel befindet sich inmitten des Intervalls [0; 90-r] und der theoretisch maximale Wirkungsgrad des Schneckengetriebes wird dann mit der folgenden Beziehung zum Ausdruck gebracht:
hmax = tan(45-r/2) / tan(45+r/2)
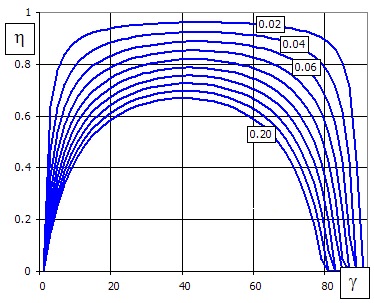
An der vertikalen Achse ist der Verzahnungswirkungsgrad, an der horizontalen Achse ist der Steigungswinkel und die einzelnen Kurven sind für verschiedene Reibungskoeffizienten.
In der Praxis wird der Steigungswinkel für die Schnecke ZA bis 10°, für
allgemeine Schnecken ZN, ZI bis zum Wert von 20-25° verwendet, und zwar vor
allem aus Fertigungsgründen. Das Bestreben um einen wo möglich größten
Wirkungsgrad, führt dann zur Anwendung von höheren Steigungswinkeln, was durch
eine Senkung des Schneckendurchmessers und durch den Einsatz von mehrgängigen
Schnecken erreichbar ist.
Bei Kraftübersetzungen wird diese konstruktive Anordnung praktisch nicht benutzt.
Das Verzahnungswirkungsgrad: hz = P1 / P2 = tan(g
- r) / tan(g)
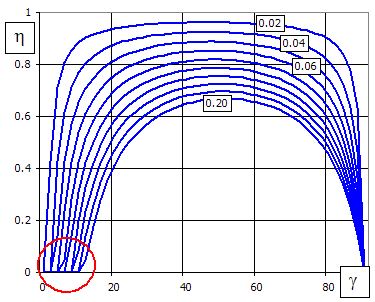
Wichtig ist jedoch in diesem Fall der Schnittpunkt der Kurve mit der horizontalen Achse (rot gekennzeichnet), der den Grenzwert der Selbsthemmung definiert, was in dem Fall besteht, wenn es nicht möglich ist die Räder durch ein noch so großes, auf das Schneckenrad wirkendes Moment in Bewegung zu setzen (es wird zum Beispiel bei Hebemechanismen benutzt). Die Selbsthemmungsgrenze wird in dem Moment erreicht, wenn der Steigungswinkel dem Reibungswinkel gleich wird.
In der Praxis wird minimal unterschieden:
Der Reibungskoeffizient beeinflusst den Wirkungsgrad der Übersetzung am meisten. Er ist abhängig von einer ganzen Reihe von Parametern (Werkstoff, Oberfläche, Schmierstoffe, Geschwindigkeit, Größe). Er wird nach der Formel berechnet:
mzm = m0T • YS • YG • YW • YR; Berechnung der Zeile [6.1-6.7]
In die Berechnung des Gesamtwirkungsgrades sind dann die Verlustleistungen in der Lagerung, Dichtung und beim Leerlauf einbezogen und es wird nach der Formel berechnet:
hges = Pw2 / (Pw2 + PV), wo PV die Gesamtverlustleistung ist; Berechnung der Zeile [6.9-6.15]
Beim Lauf der Räder kommt es zu einem Abtragverlust des Werkstoffs, was bedeutet, dass die Verminderung der Zahndicke eintritt. Dadurch leidet vor allem die Zahnflanke des Werkstoffs mit einer niedrigeren Härte (in der Regel das Rad). In den letzten Jahren wurde eine Reihe von Testen mit verschiedenen Werkstoffen, Maßen und Öltypen mit einem typischen Ergebnis vorgenommen - siehe Abbildung.
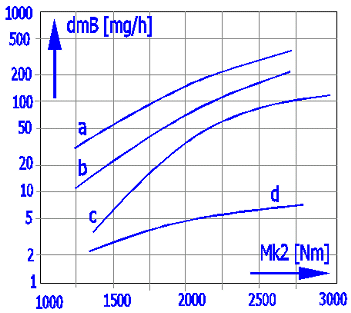
Schnecke: 16MnCr5E; Rad: CuSn12Ni-GZ; a=160mm; n1=500; i=20
Kurven:
Mineralöl: a) n40=220 [mm2/s]; b)
n40=460 [mm2/s]; c)
n40=680 [mm2/s]
Synthetisches Öl: d) EO:PO=0:1
Aus den Ergebnissen wird deutlich, dass die Verwendung von synthetischen Ölen wesentlich den Verschleiß verringert. Die Ölviskosität hat einen Einfluss lediglich bei Mineralölen damit, dass mit einer niedrigen Viskosität der Verschleiß wesentlich ansteigt.
Der genehmigte Verschleiß des Schneckenrades dWlimn hängt vor allem von der Einrichtung ab, in welcher die Schneckenübersetzung angewandt wurde. Er kann zum Beispiel durch das maximale Spiel in der Verzahnung bestimmt werden. Jedenfalls wird der Grenzwert des Verschleißes an der Grenze der Zahnspitzigkeit erreicht. Wenn keine konkreten Bedingungen vereinbart/festgelegt sind, wird in der Regel angenommen
dWlimn=0.3 • mx • cos(gm), Zeilenberechnung [7.18]
Der Verschleißgrenzwert befindet sich in einer Zelle, der übliche Wert wird nach dem Abhaken des Abhakfeldes automatisch ausgefüllt.
SW = dWlimn / dWn ≥ SWmin (SWmin=1.1)
Es ist möglich sie zu beeinflussen (erhöhen) durch die Wahl einer niedrigeren verlangten Lebensdauer [2.12], durch die Wahl eines Öls mit höherer Qualität, Wahl einer höheren Viskosität [2.7,2.8] und selbstverständlich durch die Wahl der geometrischen Parameter.
Durch eine pulsierende Belastung der Zahnflanke und Einwirkung der Gleitreibungskräfte entstehen auf der Zahnoberfläche Müdigkeitsrisse. In diese Risse gelangt das Öl und durch die Wirkung der hydrostatischen Kräfte kommt es zum Herausreißen von Oberflächenpartikeln und zu einer Grübchenbildung. Die nachfolgende Graphik bietet einen Einblick in die Entstehung von Grübchen als eine Funktion der Lastspielzahlen und des Achsabstandes. Die Formel für die Berechnung der Grübchen basiert auf einer Reihe von Testergebnissen und auf Betriebserfahrungen.
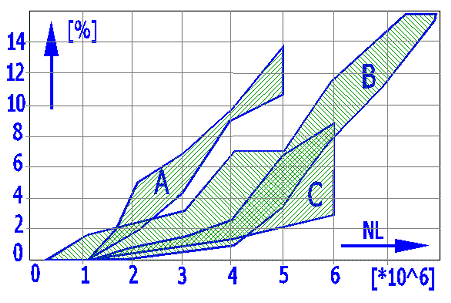
Horizontal: Lastspielzahl - Rad; Vertikal: [%] Grübchenfläche von der Fläche der Zahnflanke
Schnecke: 16MnCr5E; Rad: CuSn12Ni-GZ; Synthetisches
Öl;
n1=500;
i=20; dHm
= 330 MPa
Kurven: A) a=160 [mm]; B) a=100 [mm];
C) a=65 [mm]
Für die Sicherheitskontrolle werden folgende Grundformeln verwendet:
![]()
SH = sHG / sHm ≥ SHmin (SHmin=1.0)
Es ist möglich, sie durch die Wahl einer niedrigeren verlangten Lebensdauer [2.12], die Wahl eines Öls von einer besseren Qualität [2.7] und selbstverständlich durch die Wahl der geometrischen Parameter zu beeinflussen (zu erhöhen).
Eine zu große und dynamisch sich ändernde Durchbiegung der Schneckenwelle kann zur Interferenz und somit zum erhöhten Verschleiß führen.
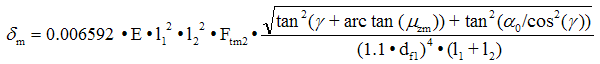
![]()
Der Wert der zulässigen Durchbiegung wurde auf der empirischen Grundlage, also aus praktischen Erfahrungen gewonnen.
Sd = dlim / dm ≥ Sdmin (Sdmin = 1.0)
Sofern es zur hohen Spannung am Zahnfuß kommt, leiden die Radzähne an einer plastischen Deformation, was zur Verschiebung des Berührungsbereichs und zum nachfolgenden Zahnbruch führt. Die Untersuchungen und Spannungsteste am Zahnfuß wurden für verschiedene Achsabstände, Übersetzungsverhältnisse, Formzahlen und diverse Werkstoffen vorgenommen. In der Abbildung befinden sich Testergebnisse und Ergebnisse der nach der Norm DIN 3996 berechneten Werte.
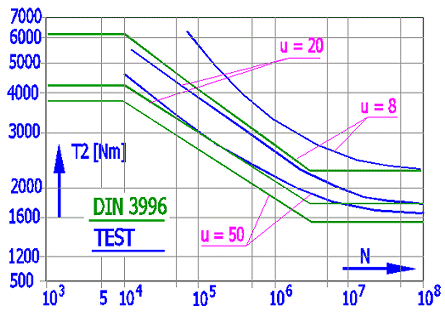
Horizontal: Lastspielzahl - Rad; Vertikal: Eingangsdrehmoment
Schnecke: 16MnCr5E; Rad: CuSn12Ni-GZ; Synthetisches Öl; a=120,u=8/20/50.
Grün: Berechnung DIN, Blau: Testergebnis, Störungswahrscheinlichkeit 50[%]
Die Teste zeigen, dass der Ausgangsdrehmoment, bei welchem es zur Zahnbeschädigung kommt, mit dem steigenden Übersetzungsverhältnis abnimmt. Dieser Moment steigt bei der abnehmenden Lastspielzahl. Die Teste zeigen gleichzeitig, dass für die aus Bronze hergestellten Räder vor der Zahnbeschädigung zuerst eine dauerhafte plastische Deformation eintritt.
tF = Ftm2 / (b2H • mx) • Yeps • YF • Yg
tFG = tFlim • YNL
Für die Zwecke der nachfolgenden Diagramme wurde der max. Grenzwert für die Leistung gemäß AGMA als der Eingangswert der Berechnung gemäß DIN verwendet.
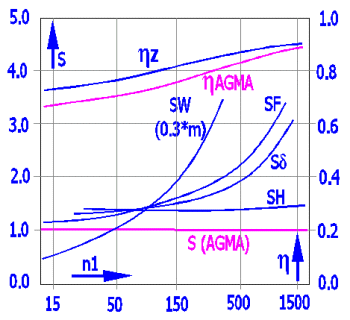
Schnecke: 16MnCrSEh; Rad: GZ-CuSn12Ni; polyglycol (EO:PO=0:1); a = 180 mm; u = 50/2; L = 25000 h
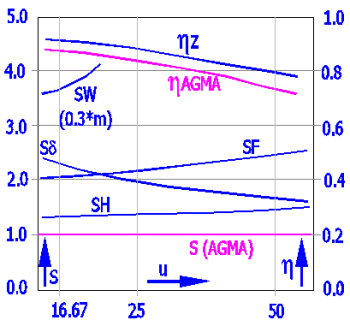
Schnecke: 16MnCrSEh; Rad: GZ-CuSn12Ni; polyglycol (EO:PO=0:1); a = 180 mm; n1 = 500 rpm; L = 25000 h
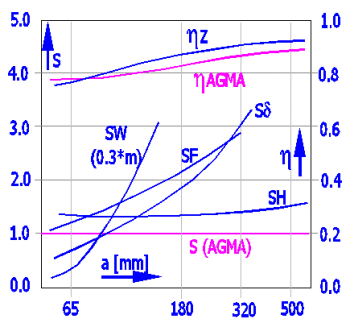
Schnecke: 16MnCrSEh; Rad: GZ-CuSn12Ni; polyglycol (EO:PO=0:1); u = 50/2; n1 = 500 rpm; L = 25000 h
Beim Entwurf eines Getriebes ist auch mit der im Inneren des Getriebegehäuses entstehenden Wärme zu rechnen (Wirkungsgrad der Verzahnung, Reibung der Lager, Reibung in der Dichtung). Dieser Parameter ist bei einer Stirn- oder Kegelverzahnung nicht all zu wichtig. Er ist jedoch bei der Schneckenübersetzung wichtig. Da der Wirkungsgrad bei einer Schneckenübersetzung wesentlich niedriger als der Wirkungsgrad einer Stirn- oder Kegelverzahnung ist, entsteht in der Verzahnung wesentlich mehr Wärme, die notwendig ist abzuführen. Aus diesem Grund hat die Temperatursicherheit eine große Bedeutung für den richtigen Entwurf, der die Funktion des Getriebes im zugelassenen Temperaturbereich des verwendeten Öls sichert. Der Temperaturentwurf/die Temperatursicherheit ist oft einer der limitierenden Faktoren beim Entwurf einer Übersetzung.
In dieser Berechnung ist außer der Orientierungsformel für die Berechnung der Aufwärmung nach der DIN 3996 auch eine einfache Temperaturanalyse aufgeführt. Diese Analyse gestattet die Berechnung der durch die Getriebewände durchdringenden Wärme und auch die Berechnung der durch die Ölkühlung abgeführten Wärme. Für Entwürfe von wichtigen Übersetzungen empfehlen wir in jedem Fall eine ausführliche thermodynamische Analyse durchzuführen, am bestem in Verbindung mit einschlägigen Testen.
In dieser Temperaturanalyse werden zwei Grundformeln angewendet
P = k • A • dT
wo:
P.....diffuse Leistung [kW]
k.....kombinierter Koeffizient des Wärmeübergangs (Wärmeabgabe, Strahlung)
[W/m2*K]
A.....Außenfläche des Getriebegehäuses [m^2]
dT...Wärmedifferenz zwischen der Öltemperatur und der Außenumgebung [°C]
Für die Festlegung des Koeffizienten k ist es möglich, in der Literatur eine Reihe von Empfehlungen zu finden. Die ausgewählten Werte finden Sie im Absatz [11.12].
Die Grundfläche A ist durch die Berechnung als ein minimaler Quader ohne Vorsprünge und Rippung, in den die vorgeschlagenen Räder hineinpassen, und der Einfluss der Rippung dann anhand eines Koeffizienten festgelegt wird.
P = c • ro • Q • dT
wo:
P.....Kühlerleistung [kW]
c.....spezifische Wärmekapazität des Öls [Ws/Kg/°K]
ro...spezifisches Gewicht des Öls [kg/dm3]
Q...Menge des durchströmenden Öls [l/s]
dT..Wärmedifferenz zwischen dem aus dem Getriebegehäuse aussteigenden Öl und
dem abgekühlten, zurück eintretenden Öl.
Die Übersetzungen mit Zahnrädern unterteilen wir auf in:
Kraftübertragendes Getriebe - Beim Räderpaar, das vor allem zur Übertragung und Umwandlung der Leistung bestimmt ist, ist die Durchführung eines Festigkeitsentwurfs/-kontrolle erforderlich (zum Beispiel Antriebe von Maschinen, Getriebe für Industrie ...).
Kraftloses Getriebe - Beim Räderpaar, bei dem das übertragene Drehmoment im Hinblick auf die Radgröße minimal ist, ist keine Durchführung vom Festigkeitsentwurf/-kontrolle erforderlich (zum Beispiel Geräte, Regelungstechnik...).
Die Aufgabe eines Schneckenräderentwurfs gestattet einen großen Spielraum in der Wahl der Durchmesser- und Breitenparameter der Zahnräder. Die Berechnung macht es deshalb möglich, eine Lösungstabelle mit entsprechender Lösung zu erstellen, und aus dieser Tabelle auf der Grundlage einer ganzen Reihe von Parametern Gewicht, Achsabstand, Wirkungsgrad und vieles andere auszuwählen.
Mit diesem Vorgang erhalten Sie eine Lösungstabelle für die entworfenen Räder.
Obwohl die Lösungstabelle richtige Entwürfe enthält, es ist angebracht einige der Parameter zu optimieren und abzugleichen. Es handelt sich vor allem um den Achsabstand [4.23,4.24] und den Lagerabstand der Schnecke [4.16,4.17].
Bei einem Kraftgetriebe ist es am günstigsten:
Für Getriebe, die keine Kräfte übertragen, ist es möglich noch Hilfsberechnungen zu verwenden [16.0].
Beim Entwurf eines Getriebes ohne Kraftübertragung ist es nicht nötig, die Festigkeitsparameter zu lösen und zu kontrollieren. Wählen Sie bitte deshalb direkt eine geeignete Zahnanzahl und Modul [4.8-4.20] und kontrollieren Sie die Abmessungen der zu entwerfenden Verzahnung.
In diesem Absatz geben Sie bitte die Grundeingangsparameter der zu entwerfenden Verzahnung ein.
Im Auswahlverzeichnis wählen Sie das verlangte Einheitssystem der Berechnung aus. Bei der Umschaltung der Einheiten werden sofort alle Werte umgerechnet.
Im Auswahlverzeichnis wählen Sie das angetriebene Element aus (Schnecke oder Rad).
Geben Sie bitte die verlangte Leistung am Schneckenrad ein. Die üblichen Werte bewegen sich im Bereich 0.1-300kW / 0.14-420HP, in Extremfällen bis zu 1000kW / 1400HP. Mit der Taste rechts müssen Sie die maximale Leistung nachrechnen, welche das gegebene Schneckengetriebe in der Lage ist, zu übertragen.
Geben Sie bitte die Drehzahl der Schnecke ein. Übliche Schneckendrehzahl bis zu 3000/min, extreme Drehzahlen können bis zu 40000/min sein. Die Drehzahlen des Schneckenrades werden aus der Zahnanzahl der beiden Räder berechnet.
Es handelt sich um ein Ergebnis der Berechnung und es ist nicht möglich dieses einzugeben.
Das optimale Übersetzungsverhältnis bewegt sich im Bereich von 5-100. In extremen Fällen kann es auch den Wert bis zu 300 (1000 kraftlose Räder) erreichen. Das Übersetzungsverhältnis geben Sie im linken Eingangsfeld der Tastatur ein. Im rechten aufzumachenden Verzeichnis befinden sich die empfohlenen Werte des Übersetzungs-verhältnisses und bei der Auswahl aus diesem Verzeichnis wird der ausgewählte Wert automatisch ins Feld auf der linken Seite eingefügt.
Da das wirkliche Übersetzungsverhältnis ein Anteil der Zähneanzahl der beiden Räder (ganze Zahlen) ist, weicht meistens das wirkliche Übersetzungsverhältnis von dem verlangten (eingegebenen) Verhältnis ab. Der Wert des "wirklichen Übertragungsverhältnisses“ wird links angeführt, rechts ist dann die prozentuelle Abweichung von dem verlangten Übertragungsverhältnis.
Beim Entwurf einer kraftübertragenden Übersetzung geben Sie in diesem Absatz weitere ergänzende Betriebs- und Herstellungseingangsparameter an. Bemühen Sie sich, bei der Wahl und Eingabe dieser Parameter möglichst genau zu sein, weil jeder dieser Parameter einen dramatischen Einfluss auf die Eigenschaften des zu entwerfenden Räderpaares haben kann.
Die Tragfähigkeit der Schneckenräder ist durch verschiedene Bedingungen begrenzt:
An diese Bedingungen ist auch die Wahl des Werkstoffs der Schnecke und des Rades anzupassen. Es werden meistens eine gehärtete und geschliffene Schnecke gegenüber einem Rad aus Zinn oder Phosphorbronze gewählt.
Der Grundwerkstoff ist die Bronze, seltener ist es Guss oder Messing. Räder aus Kunststoff werden für niedrigere Leistungen verwendet (sie dämpfen Schläge, niedrigeres Laufgeräusch) und Übersetzungen, die keine Kräfte übertragen. Räder aus Bronze werden aus Spargründen als zusammengebaute Räder hergestellt (der Bronzekranz wird auf ein Stahl- oder Eisengussrad aufgesetzt). Geeignet ist auch der Schleuderguss.
Optimal sind Bronze mit Zinn mit einem hohen Gehalt an Sn 10-12% (ausgezeichnete Reibungseigenschaften, hohe Standfestigkeit gegenüber Festfressen und ein gutes Formfüllungsvermögen), sie sind jedoch teuer. Deren Einsatz kann nur bei beanspruchbaren Übersetzungen begründet werden und bei einer mehr als 10 m/s großen Schubgeschwindigkeit. Jedoch auch in diesen Fällen gibt es Versuche, diese Metalle durch Bronze Sn-Ni und andere zu ersetzen. Für Geschwindigkeiten v=4-10 m/s ist es möglich Bronze mit einem niedrigeren Gehalt an Sn (5-6 %) zu benutzen.
Bei Geschwindigkeiten v<4 m/s ist billigere Bronze ohne Zinn-Zusatz mehr geeignet, z.B. Aluminiumbronze oder Bleibronze und Messing. Sie besitzen eine verhältnismäßig hohe Härte und Festigkeit, sind jedoch weniger standfest gegenüber dem Festfressen und sie lassen sich schlechter einfahren. Die mit eingreifende Schnecke ist deshalb mit einer hohen Oberflächenhärte (HRC>45) auszurüsten. Bei Schneckenrädern mit einem größeren Schneckenrad ist aus Spargründen die Kombination der Bronzeschnecke und des Gussrades möglich.
Für kleine Leistungen, ruhige Belastung und kleine Umfangsgeschwindigkeiten bis zu 2 m/s ist es möglich, den Grauguss in Zweierkombination mit einer Stahlschnecke einzusetzen.
Für Schnecken wird kohlenstoffreicher oder legierter Stahl verwendet, der eine thermische Aushärtung der Oberfläche gestattet (Härten auf HRC 45-50, Zementieren und Härten auf HRC 56-62 und Nitrierhärten). Die Zahnflanken werden geschliffen, gegebenenfalls poliert. Bei Nitrierhärten kann das Schleifen wegfallen und es genügt lediglich das Polieren. Stahlschnecken im veredelten Zustand oder im Feinglühen können nur für kleinere Leistungen und kleinere Umfangsgeschwindigkeiten eingesetzt werden.
Eigene Werkstoffwerte – Wenn Sie für die Herstellung einer Verzahnung einen Werkstoff verwenden wollen, der in der gelieferten Tabelle der Werkstoffe nicht vorliegt, ist es erforderlich über den eigenen Werkstoff eine Reihe von Angaben einzugeben. Schalten Sie ins Blatt "Werkstoffe" um. Die ersten 5 Zeilen in der Werkstofftabelle sind für die Definition eigener Werkstoffe vorbehalten. In die für die Werkstoffbenennung bestimmten Spalte geben Sie den Werkstoffnamen ein (er wird im Bezugsblatt dargestellt) und schrittweise füllen Sie alle Parameter auf der Zeile aus (weiße Felder). Nach dem Ausfüllen schalten Sie wieder ins Blatt "Berechnung" um und übernehmen den neu definierten Werkstoff und dann setzen Sie in der Berechnung fort.
Wählen Sie den Schneckentyp aus. Details über Schneckentypen finden Sie im theoretischen Teil der Hilfe.
Die Einstellung dieser Parameter beeinflusst wesentlich die Berechnung der Sicherheitsfaktoren. Deshalb suchen Sie nach der besten Spezifikation bei der Auswahl der Belastungstypen. Beispiele der Antriebsmaschinen:
Die Einstellung dieser Parameter beeinflusst wesentlich die Berechnung der Sicherheitsfaktoren. Deshalb suchen Sie bei der Auswahl der Belastungstypen nach der besten Spezifikation. Beispiele der Antriebsmaschinen:
Die Schmierungsart der Räder und die Kühlungsart des Getriebes (oder des Öls bei der Druckschmierung) ist von einer ganzen Reihe von Bedingungen abhängig, wie die übertragene Leistung, das Übersetzungsverhältnis, die Drehzahl, der Werkstoff, die Bauart des Getriebegehäuses, Bestimmungen usw. Beim Entwurf ist es möglich, von der Umfangsgeschwindigkeit der Schnecke auszugehen, in der Finalkonstruktion ist jedoch erforderlich alle Bedingungen zu berücksichtigen.
Tauchschmierung: 0-4 [m/s] (0-13 [ft/s])
Einspritzschmierung: 2-10 [m/s] (6-33 [ft/s])
Umlaufdruckschmierung: 8 und mehr [m/s] (25 [ft/s])
Für wenig beanspruchte Übersetzungen ist es möglich ein Mineralöl zu wählen, bei höheren Geschwindigkeiten, größeren übertragenen Leistungen und höheren Ansprüchen an Effektivität ist es günstiger, synthetisches Öl zu verwenden.
Einige Vorteile der synthetischen Öle
Dem gegenüber steht ein höherer Preis, mögliche Probleme mit Plast- oder Gummiteilen, beschränkte Mischbarkeit mit Mineralöl.
In der Auswahlliste sind die Öle nach der Viskositätsstufe ISO (AGMA) geordnet. Mit der Auswahl eines Öls aus der Liste werden die Parameter des ausgewählten Öls in die entsprechenden Zellen übertragen (Viskosität bei 40 °C, Viskosität bei 100 °C, spezifische Dichte [kg/dm^3]). Wenn Sie die Ölparameter aus dem Werkstoffblatt des Herstellers kennen, geben Sie die Parameter in die entsprechenden Zellen ein [2.9,2.10].
| Arbeitstemperatur [°C] | Schubgeschwindigkeit [m/s] | |||
| Max. Arbeitstemp | Starttemp | < 2.5 | 2.5 ... 5 | >5 |
| 0 - 10 | -10 - 0 | 110 … 130 | 110 … 130 | 110 … 130 |
| 0 - 10 | >0 | 110 … 150 | 110 … 150 | 110 … 150 |
| 10 - 30 | >0 | 200 … 245 | 150 … 200 | 150 … 200 |
| 30 - 55 | >0 | 350 … 510 | 245 … 350 | 200 … 245 |
| 55 - 80 | >0 | 510 … 780 | 350 … 510 | 245 … 350 |
| 80 - 100 | >0 | 900 … 1100 | 510 … 780 | 350 … 510 |
| AGMA no of Gear Oil | ISO Viscosity Grade | |
| R & O | EP | |
| 1 | VG 46 | |
| 2 | 2 EP | VG 68 |
| 3 | 3 EP | VG 100 |
| 4 | 4 EP | VG 150 |
| 5 | 5 EP | VG 220 |
| 6 | 6 EP | VG 320 |
| 7 7comp | 7 EP | VG 460 |
| 8 8comp | 8 EP | VG 680 |
| 8A comp | VG 1000 | |
| 9 | 9 EP | VG 1500 |
Geben Sie den Wert aus dem Werkstoffblatt des Ölherstellers ein.
Geben Sie den Wert aus dem Werkstoffblatt des Ölherstellers ein.
Geben Sie den Rauheitswert ein. Für einsetzbare Bearbeitungsarten ist es möglich zu erreichen Ra:
Er ist auf der Grundlage der Ungleichmäßigkeit der Belastung von der angetrieben / Antriebsmaschine vorgeschlagen [2.4,2.5]. Nach dem Abhaken des Abhakfeldes wird der Wert automatisch ausgefüllt. Mit dem Koeffizienten KA wird der Wert des Drehmoments multipliziert.
Der Parameter bestimmt die verlangte Standzeit in Stunden. Orientierungswerte in Stunden sind in der Tafel angeführt.
|
Anwendungsbereich |
Dauerhaltbarkeit |
| Haushaltsmaschinen, nur selten benutzte Anlagen | 2000 |
| Elektrische Handwerkzeuge, Maschinen für kurzzeitigen Betrieb | 5000 |
| 8-Stundenbetrieb | 20000 |
| 16-Stunden-Betrieb | 40000 |
| Maschinen für durchgehenden Betrieb | 80000 |
| Maschinen für durchgehenden Betrieb mit langer Lebensdauer | 150000 |
In die Zeilen [2.14-2.17] geben Sie die verlangten Sicherheitskoeffizienten ein. Bei der Berechnung der Lösungs-tabelle [4.1] werden in die Tabelle lediglich die Lösungen eingeordnet, welche die verlangten Sicherheitskoeffizienten erfüllen. Die empfohlenen Werte werden rechts vom Eingabefeld angeführt.
Es ist möglich, die Parameter des Verzahnungsprofils in einem breiten Bereich zu ändern und sie sind oft von den Fertigungsmöglichkeiten abhängig. Geläufig werden die nachfolgenden Möglichkeiten benutzt:
Koeffizient der Zahnkopfhöhe ha* = 1.0
Einheitskopfspiel ca* = 0.25 (0.2,0.3)
Koeffizient des Zahngrundradius rf* = 0.38
Dies ist der zentrale Abschnitt der gesamten Berechnung und des Geometrieentwurfs der Schneckenräder. Er ist unterteilt in drei untereinander sehr eng zusammenhängende Teile.
Die Lösungstabelle ist wie folgt gebildet: In die Berechnung werden schrittweise die Anzahl der Schneckengänge eingesetzt (den Bereich stellen Sie in [4.3] ein), für jeden Wert wird die Formzahl q schrittweise eingesetzt (den Bereich stellen Sie in [4.4] ein) und für jede dieser Kombinationen wird der minimale Wert des Moduls gesucht (bzw. der maximale Wert DP für die Zoll-Einheiten), der die verlangten Sicherheitskoeffizienten erfüllt (Auswahl in [4.2] ). Nach dem Auffinden aller ausreichenden Lösungen wird die Tabelle nach dem auf der Zeile [4.5] eingestellten Parameter geordnet und in die Berechnung ist die erste Lösung aus der Tabelle eingegeben [4.7].
Den Beginn der Tabellenberechnung starten Sie mit der Taste "Tabelle starten". Der Berechnungsablauf ist im Dialog dargestellt.
In dieser Zeile haken Sie ab, welcher Sicherheitstyp erfüllt werden muss, damit die Lösung in die Lösungstabelle einbezogen wird. Die Koeffizientengröße stellen Sie in den Zeilen [2.14-2.17] ein. Wir empfehlen die Kontrolle aller Koeffizienten eingeschaltet zu haben.
In dieser Zeile geben Sie ein, für welchen Bereich der Anzahl der Schneckengänge z1 die Tabelle zu lösen ist. Geläufig wird z1=1~4 verwendet (für ein höheres Übersetzungsverhältnis eine höhere Anzahl der Schneckengänge z1).
Der Bereich der erlaubten Werte ist z1=1~12, der erste Wert muss kleiner oder dem anderen Wert gleich sein.
In dieser Zeile geben Sie ein, für welchen Bereich der Formzahl q die Tabelle zu lösen ist. Geläufig wird benutzt q=8-16 (für einen kleineren Modul ein höherer Wert q).
Der Bereich der erlaubten Werte ist q=6~25, der erste Wert muss kleiner oder dem anderen Wert gleich sein.
Wählen Sie aus, nach welcher Spalte der Tabelle die Tabelle zu ordnen ist.
Mit der Auswahl einer Lösung aus der Tabelle werden die Lösungsparameter in die Berechnung übertragen. Die kleine Taste "<" rechts überträgt in die Berechnung die Werte aus der aktuellen Tabellenzeile.
Die Tabelle enthält folgende Parameter:
In diesem Teil können Sie direkt alle wichtigen Parameter der Schneckenräder definieren, welche direkt dessen Geometrie beeinflussen und definieren. Die Beschreibung und Bedeutung der einzelnen Parameter wird bei jedem von ihnen angeführt.
Geben Sie die Anzahl der Zähne (der Gänge) der Schnecke ein. Normal wird der Wert im Bereich 1 bis 4 benutzt, in Sonderfällen kann er bis zu 12 sein. Für die geeignete Wahl der Anzahl der Zähne empfehlen wir die Auswahl aus der Lösungstabelle [4.6] auf der Grundlage Ihrer Optimierungsparameter (zum Beispiel Gewicht, Wirkungsgrad, Achsabstand...). In jedem Fall ist es angebracht, mit dem Verfahrenstechniker die Fertigungsmöglichkeiten zu konsultieren.
Die Anzahl der Zähne des Schneckenrades wird auf der Grundlage des verlangten Übersetzungsverhältnisses nachgerechnet. Die Anzahl der Zähne des Rades muss bestimmte minimale Werte annehmen, ansonsten würde es zum Freischnitt kommen. Sollte eine solche Situation entstehen, wird in der Klammer der minimale Wert angezeigt und der Text in der Zelle ist rot abgebildet.
Für die Schnecke vom Typ ZA wird ein axialer Eingriffswinkel eingegeben, für die sonstigen Typen (ZN,ZI,ZK,ZH) ein normaler Eingriffswinkel. Der Eingriffswinkel wird aus dem Bereich 15º bis 30º gewählt.
Normal wird der Wert von 20º benutzt. Es ist möglich den Eingriffswinkel in Abhängigkeit an die Anforderungen auf die konstruierte Anlage zu wählen. Ein größerer Eingriffswinkel führt zu einer erhöhten Zahnbruchsicherheit (SF) und zur Senkung der Gefahr eines Freischnitts der Radzähne. Anderseits reduziert ein größerer Eingriffswinkel die Anzahl der Zähne im Eingriff, erhöht die Lagerbelastung und erhöht die Schneckenbelastung auf die Biegung (eine höhere Durchbiegung der Schnecke). Der Eingriffswinkel kann auch in Anhängigkeit vom Steigungswinkel [4.13] damit gewählt werden, dass für einen größeren Steigungswinkel ein größerer Eingriffswinkel gewählt wird.
Minimale Anzahl der Radzähne in Abhängigkeit vom Eingriffswinkel bei einer Nullkorrektur der Verzahnung (Tabelle in der Hilfe).
| Eingriffswinkel [º] | Min. z2/NG |
| 14.5 | 40 |
| 17.5 | 27 |
| 20 | 21 |
| 22.5 | 17 |
| 25 | 14 |
| 27.5 | 12 |
| 30 | 10 |
q=d1/m
Bei der gewählten Anzahl der Zähne bei der Schnecke z1 und dem bekannten Wert des Moduls (mx bzw. mn) ist der Schneckendurchmesser d1 praktisch beliebig, sofern nicht ein bestimmter Wert des Steigungswinkels g gefordert wird. Die Hersteller, bemüht um eine möglich niedrige Anzahl der Schraubenfräsen bei der Herstellung der Verzahnung der Schneckenrädern, empfehlen d1=q•m zu wählen, wo q ein von der Größe des normalisierten Moduls m abhängiger Faktor ist. Im Hinblick auf die Biegesteifheit der Schnecke werden zu kleinen Werten m größere Werte q zugeordnet.
| m | 2 | 2.5 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | 16 | 20 | 25 |
| q | 16 | 12 | 12 | 9 | 9 | 9 | 8 | 8 | 8 | 8 | 8 | 6 |
| 14 | 10 | 10 | 10 | 9 | 10 | 10 | ||||||
| 12 | 12 | 12 | 10 | |||||||||
| 14 | 14 | 14 | 12 |
d1=q•m
Wenn Sie den genauen Wert des Schneckendurchmessers eingeben müssen, aktivieren Sie das Eingansfeld durch das Abhaken der Wahltaste. Der empfohlene Annäherungswert d1 in Abhängigkeit vom Modul und Anzahl der Zähne der Schnecke ist rechts vom Eingangsfeld angeführt.
Der Steigungswinkel ist einer der Schlüsselparameter der Schneckenverzahnung, welcher mit den Abmessungen der Schnecke und mit dem Wirkungsgrad der Übersetzung eng zusammenhängt. Mit wachsendem Steigungswinkel steigt auch der Wirkungsgrad (Details im Kapitel über den Wirkungsgrad).
Ein wichtiger Steigungswinkel befindet sich an der Selbsthemmungsgrenze (Reibungswinkel [6.8] ist dem Steigungswinkel gleich). Dieser Winkel wird nach der Betätigung der Taste "<=SL" rechts ausgefüllt.
6º-40º bei im Ganzen hergestellten Schnecken
bis 17º bei Schnecken auf einer Welle aufgesetzt
Wählen Sie die Steigungsrichtung der Schnecklinie aus. Sie hat Einfluss lediglich auf die Orientierung der Kräfte und auf die Drehrichtung. Sofern es die Kinematik des Antriebs nicht verlangt, hat die Schnecke die rechte Steigungsrichtung.
Der Modul (DP) ist ein Schlüsselparameter, der die Rädergröße und somit auch die einschlägigen Sicherheits-koeffizienten beeinflusst. In Abhängigkeit von den ausgewählten Einheiten der Berechnung [1.1] wird der Eingang verlangt:
Es wird der Verzahnungsmodul verlangt; Achsmodul mx für den Schneckentyp ZA und Normalmodul mn für sonstige Typen (ZN,ZI,ZK,ZH).
Es wird der Wert DP verlangt (Diametral Pitch).
Der Tabellenwert kann der Auswahlliste rechts entnommen werden.
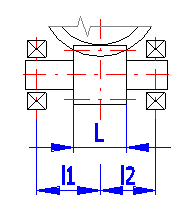
Der Lagerabstand ab der Schneckenmitte (siehe Abbildung) hat einen direkten
Einfluss auf die Durchbiegung der Schnecke und somit auch auf die
Durchbiegesicherheit. Auf der Zeile [4.17] geben Sie die Lagerabstände der
Schneckenwelle von der Radmitte in Prozent des Außendurchmessers des
Schneckenrades an. Diese Auswahlweise wird automatisch bei der Berechnung der
Lösungstabelle angewendet [4.6]. Wenn Sie einen genauen Wert eingeben wollen,
haken Sie das Abhakfeld auf der Zeile [4.18] ab und geben sie den genauen Wert
ein.
Auf der Grundlage des Moduls und der Anzahl der Zähne wird die Verzahnungslänge automatisch entworfen. Wenn Sie einen eigenen Wert eingeben möchten, haken Sie das Abhakfeld rechts ab.
Auf der Grundlage des Schneckendurchmessers wird die Radbreite automatisch entworfen. Wenn Sie einen eigenen Wert eingeben möchten, haken Sie das Abhakfeld rechts ab.
Die Schnecke wird grundsätzlich ohne Korrektur angefertigt. Es wird lediglich das Schneckenrad korrigiert, wobei der Hauptgrund für die Benutzung einer Korrektur(Verschiebung des Fertigungswerkzeuges) das Erreichen des verlangten (normalisierten) Achsabstandes ist. Seltener kommt die Benutzung einer Korrektur zur Beseitigung eines Freischnitts des Zahnfußes oder zur Verbesserung der Biegefestigkeit des Zahns vor.
Rechts von der Eingangszelle ist der Minimalwert des Profilverschiebungsfaktors, der den Freischnitt des Zahnfußes verhindern soll. Ist der aktuelle Wert kleiner, ist der Wert rot dargestellt. Der minimale Profil-verschiebungsfaktor hängt von der Anzahl der Radzähne [4.9] und von dem Eingriffswinkel ab [4.10].
Die häufigste Aufgabe ist der Entwurf der Schneckenübersetzung mit dem gegebenen Achsabstand. Beim Entwerfen empfehlen wir das nachfolgende Vorgehen:
Der Achsabstand kann durch eine Reihe von Parametern beeinflusst werden. In dieser Berechnung können Sie auswählen:
Bei jeder Art ist in Klammern "<>" der mögliche Veränderungsbereich eines Parameters angeführt und in Klammern "( )" ist der mögliche Veränderungsbereich des Achsabstandes angeführt.
Im ersten Feld ist das Gewicht des kompletten Getriebes (Summe des Gewichts der Übersetzungsräder, Wellen und des Getriebegehäuses). Im zweiten Feld ist lediglich das Gewicht der Schnecke und des Rades einschließlich der Wellen. Bei der Berechnung des Gewichts des Getriebegehäuses wird als Werkstoff Eisenguss in Betracht gezogen.
Im ersten Feld ist der Gesamtwirkungsgrad der aktuell entworfenen Schneckenräder, im rechtem Feld dann das maximal mögliche für die aktuellen Bedingungen (Schmierung, verwendete Werkstoffe, Lagerung usw.).
Der Gesamtwirkungsgrad ist am meisten durch den Steigungswinkel beeinflusst [4.13], wenn ein höherer Steigungswinkel zum höheren Wirkungsgrad führt.
In diesem Absatz sind sämtliche Verzahnungsgrundmaße übersichtlich ausgeschrieben. Die verwendeten Formeln, Abbildungen und weitere Informationen finden Sie im theoretischen Teil der Hilfe.
Es handelt sich um den größten Durchmesser des Schneckenrades, wobei der empfohlene Orientierungswert gemäß DIN 3975 ist: de2=da2+mx, der auch voreingestellt ist. Der minimale und maximale Wert ist im grünen Feld rechts angeführt.
Sofern Sie einen eigenen Wert eingeben möchten, haken Sie das Abhakfeld auf dieser Zeile ab.
Dieser Absatz enthält die Berechnung des Wirkungsgrades einer Verzahnung und die Berechnung sämtlicher zusammenhängenden Parameter. Die verwendeten Formeln, Abbildungen und weitere Informationen finden Sie im theoretischen Teil der Hilfe.
Einer der Parameter, der den Gesamtwirkungsgrad beeinflusst, sind auch die Lagerverlustleistungen. Dieser Wert wird durch den Lagertyp sowie die Lagerungsart beeinflusst. Aus der Auswahlliste entnehmen Sie, mit welcher Methode die Schneckenwelle gelagert ist.
In diesem Absatz ist die Berechnung der Verschleißsicherheit angeführt. Mehr detaillierte Informationen befinden sich im theoretischen Teil der Hilfe.
Der Grenzwert des Abtrages beim Schneckenrad dWlimn hängt vor allem von der Anlage ab, in der die Schneckenübersetzung eingesetzt ist. Er kann zum Beispiel durch das maximale Spiel in der Verzahnung bestimmt werden. Im jeden Falle wird jedoch der Grenzwert des Abtrages an der Spitzigkeitsgrenze des Zahnes erzielt. Sofern keine konkreten Bedingungen vereinbart/festgesetzt sind, werden sie als normale angenommen.
dWlim=0.3 • mx • cos(gm).
Der Grenzwert des Abtrages befindet sich in der grünen Zelle, der normale Wert wird nach dem Ausfüllen des Abhakfeldes automatisch ausgefüllt.
Es ist möglich, sie mit der Wahl einer niedrigeren verlangten Standzeit [2.12], Wahl eines Öls mit höherer Qualität, Wahl einer höheren Viskosität [2.7,2.8] und selbstverständlich durch die Wahl der geometrischen Parameter, zu beeinflussen (zu erhöhen).
In diesem Absatz ist die Berechnung der Grübchenfestigkeit angeführt. Mehr detaillierte Informationen befinden sich im theoretischen Teil der Hilfe.
Im Absatz sind die Berechnung der Durchbiegung der Schneckenwelle und die Auflagerreaktionen (Lagerbelastung). Mehr detaillierte Informationen befinden sich im theoretischen Teil der Hilfe.
In diesem Absatz ist die Berechnung der Zahnfußtragfähigkeit angeführt. Mehr detaillierte Informationen befinden sich im theoretischen Teil der Hilfe.
Geben Sie die Zahnkranzdicke ein. Der minimale empfohlene Wert wird automatisch so ergänzt, dass der Kranzdickenfaktor YK=1.0 beträgt.
Ein höherer Lebensdauerfaktor ist bedingt mit größeren plastischen
Deformationen, welche lediglich für Verzahnungen mit einer niedrigeren
Genauigkeitsstufe akzeptabel sind. Bei der Forderung einer höheren
Zuverlässigkeit ist es angebracht, den Lebensdauerfaktor auf YNL=1.0
einzustellen. Beim Abhaken mit dem Tastensymbol wird automatisch der Wert
hervorgehend aus dem zu verwendeten Werkstoff, der Lastspielzahl und der
ausgewählten Genauigkeitsstufe ergänzt.
In diesem Absatz befinden sich die Instrumente für die Berechnung und Kontrolle der energetischen Bilanz des Getriebes. Da der Wirkungsgrad der Schneckenübersetzung wesentlich niedriger als der Wirkungsgrad einer Stirn- oder Kegelverzahnung ist, entsteht in der Verzahnung wesentlich mehr Wärme, welche abzuführen ist. Deshalb hat die Temperatursicherheit eine enorme Bedeutung für den richtigen Entwurf, welche die Getriebefunktion in den Grenzwerten des Temperaturbereiches für das benutzte Öl absichert.
Im ersten Teil ist die Berechnung der Temperatursicherheit gemäß DIN 3996 Methode C, im zweiten Teil ist die Temperaturanalyse der Schneckenübersetzung. Mehr detaillierte Informationen befinden sich im theoretischen Teil der Hilfe.
Geben Sie die Umgebungstemperatur ein. Gewöhnlich 20°C [68°F].
Die gewöhnlichen Maximalwerte sind für:
Die Temperatur wird entsprechend dem ausgewählten Öltyp automatisch eingesetzt. Wenn Sie einen eigenen Wert eingeben möchten, haken Sie es mit der Abhaktaste ab.
Suchen Sie aus, ob ein auf der Schneckenwelle aufgesetzte Ventilator verwendet wird oder ob das Getriebegehäuse ohne Ventilator ist.
Gemäß DIN 3996 ist es möglich, eine annähernde Formel für die Berechnung der Temperatur eines sehr gut gerippten Getriebegehäuses aus Eisenguss mit Achsabstand 63-400 [mm], Schneckendrehzahl 60-3000 [/min] und mit einem Übersetzungsverhältnis 10-40 anzuwenden. Bei dieser Formel ist es notwendig mit einer Abweichung +- 10°K vom wirklichen Wert zu rechnen.
Das Ergebnis der annähernden Formel gibt die Gehäusetemperatur [11.6] und Temperatursicherheit [11.7] an, die größer als 1.1 sein soll.
Dieser Teil gestattet eine einfache Temperaturanalyse des Getriebes. Die meisten Eingangsparameter sind auf der Grundlage der Größe, der übertragenen Leistung, der Konstruktionstyps und weiterer eingeschätzt. Nichtsdestoweniger ist es möglich auch genauere Werte zu verwenden, welche Sie zum Beispiel aus der Messung an einem ähnlichen Getriebe oder aus der Fachliteratur gewinnen. Für die Eingabe eines eigenen Wertes des ausgewählten Parameters haken Sie diesen auf der jeweiligen Zeile mit der Abhaktaste an.
Sie wird auf der Grundlage des verwendeten Öls so vorgeschlagen, dass der Koeffizient der Temperatursicherheit 1.1 erreicht wird.
In der Auswahlliste suchen Sie den Oberflächentyp (Bauweise) des Gehäuses. Der Parameterhaben Einfluss auf die Einschätzung der Oberfläche [11.11].
Die Oberfläche wird durch eine annähernde Berechnung auf der Grundlage der Verzahnungsmaße entnommen. Für die genaue Berechnung (bzw. Kontrolle) ist es angebracht den geeigneten Ausgang aus CAD 3D Modell anzuwenden.
Die Wärmedurchgangszahl (Austausch, Strahlung) hängt von der Umgebung der Anbringung des Getriebes (Lüftung, Raumgröße), der Größe, Berippung, Schneckendrehzahl, Temperatur usw. ab. Der Einsatz eines Ventilators kann dann diese Zahl bis auf das Dreifache erhöhen. Eine genaue Berechnung dieser Zahl ist deshalb schwierig und setzt eine gründliche Analyse voraus. In der Praxis wurden Werte von 5 [W/m2*K] bis 50 [W/m2*K] gemessen. Wenn Sie mit der Abhaktaste abhaken, wird der auf der Grundlage der Drehzahl, Größe und Bauart des Getriebes eingeschätzte Orientierungswert automatisch ergänzt.
Grundwerte für ein Gehäuse ohne Ventilator:
- Kleine nicht gelüftete Räume ...8-12 [W/m2*K]
- Gut gelüftete Räume…………...14-20 [W/m2*K]
Einfluss des Ventilators: Der Einsatz eines Ventilators kann die Zahl bis um
100% erhöhen
Einfluss der Größe: Kleine Gehäuse können diese Zahl bis um 50% größer, als
große Gehäuse haben
Einfluss der Temperatur: Mit steigender Differenz der Außen- und der
Öltemperatur kann diese Zahl bis um 15% ansteigen
Einfluss der Drehzahl: Mit steigender Drehzahl der Schnecke wächst diese Zahl
Bei Getrieben, bei dem es einen größeren Wärmeverlust gibt (größere Leistung, niedriger Wirkungsgrad), reicht oft nicht die natürliche Kühlung und es ist notwendig eine Zusatzkühlung einzusetzen. Dies kann sowohl in Form eines externen Ölkühlers sein, als auch im Form z. B. einer Kühlschnecke im Innern des Getriebes. Die für das Erreichen der verlangten Temperatur notwendige Verlustleistung [11.9] ist in dieser Zeile angeführt. Wenn die Zusatzkühlung nicht verlangt wird, ist dieser Wert Null.
Wenn die Schmierung durch Einspritzung gewählt ist [2.6], ist es möglich in diesem Teil die Menge des Kühlöls durch eine gelieferte Pumpe vorzuschlagen.
Wählen Sie in dieser Zeile, ob ein Ölkühler benutzt / nicht benutzt wird. Die Benutzung des Ölkühlers übt einen Einfluss auf die Temperatur des Schmieröls aus.
Es handelt sich um die Temperaturdifferenz zwischen dem von der Pumpe angesaugten Öl und dem eingespritzten Öl.
Die normalen Werte sind für:
Der Wert für das Schmieröl ist auf 1900 Ws/Kg/°K [0.454 BTU/lb/°F] voreingestellt.
Auf der Grundlage der ausgefüllten Parameter [11.8-11.15] wird eine solche Menge des Einspritzöls vorgeschlagen, welche die Kühlung der Übersetzung auf die verlangte Temperatur gewährleistet [11.8]
Diese sollte kleiner als der Grenzwert sein [11.2]
Der Wert sollte höher als 1.1 sein.
In diesem Absatz ist die Berechnung der Maße nach AGMA 6022-C93 angeführt. Da der Schneckenräderentwurf einen großen Spielraum gestattet, können einige der Maßparameter gemäß DIN und gemäß AGMA abweichend sein.
Vollständigkeitshalber wird hier die Festigkeitsberechnung (Kontrolle) nach AGMA angeführt. Im Vergleich mit der Berechnung nach DIN ist die Berechnung nach AGMA wesentlich einfacher, da sie eine kleinere Menge von Eingangs-parametern einbezieht. Dies beeinflusst selbstverständlich die Genauigkeit der Berechnung. Wir empfehlen deshalb eher die Kontrolle nach DIN zu nutzen, welche genauer ist und besser das Verhalten der Schneckenübersetzung beschreibt. Den Vergleich beider Methoden finden Sie im theoretischen Teil.
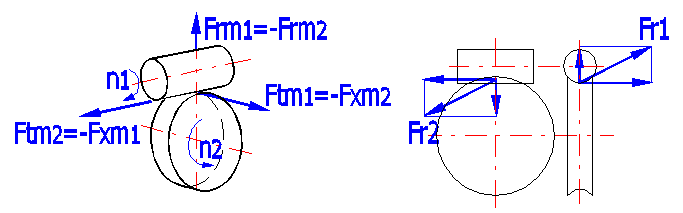
Im belasteten Getriebe entstehen Kräfte, welche auf die Konstruktion der Maschine übertragen werden. Für eine richtige Dimensionierung der Anlage ist die Kenntnis dieser Kräfte von grundsätzlicher Bedeutung. Die Orientierung der Kräfte ist in der Abbildung dargestellt, die Größe der Kräfte ist in diesem Absatz angeführt [14.1-14.6].
In diesem Absatz werden die Werkstoffcharakteristiken des Ritzel- und Rades aufgelistet.
Dieser Absatz enthält die Berechnung der Parameter, welche zum Erreichen des verlangten genauen Achsabstandes notwendig sind. In die Zeile [16.1] geben Sie Anzahl der Gänge der Schnecke und die Anzahl der Zähne des Schneckenrades ein. In der Zeile [16.2] geben Sie den verlangten Achsabstand ein und klicken Sie auf die Taste "Berechnungsstart". Die Berechnung kann auch mehrere Sekunden dauern und nach deren Abschluss ist die Lösungstabelle in der Zeile [16.4] ausgefüllt. Nach der Auswahl der entsprechenden Variante aus der Tabelle werden die Parameter (z1,z2,modul,q,x) in die Hauptberechnung übertragen.
In diesem Absatz werden die Wellendurchmesser (Stahl) vorgeschlagen, welche der verlangten Belastung entsprechen (übertragene Leistung, Drehzahl). Diese Werte haben lediglich eine Orientierungsaussage, für den definitiven Entwurf ist es angebracht eine genauere Berechnung zu benutzen.
In diesem Absatz sind Hilfsberechnungen verfügbar. Beim Eingeben der Werte benutzen Sie dieselben Einheiten wie in der Hauptberechnung. Die Übertragung der eingegebenen und berechneten Werte in die Hauptberechnung führen sie durch das Klicken auf die Taste "OK" durch.
Die Informationen über die Möglichkeiten der 2D- und 3D-graphischen Ausgabe und die Informationen über das Zusammenwirken mit den 2D- und 3D CAD-Systemen finden Sie im Dokument "Grafische Ausgabe, CAD - Systeme".
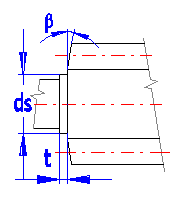
Geben Sie die Werte entsprechend der Abbildung ein, und sofern Sie dies mit der Abhaktaste abhaken, werden die Werte automatisch ausgefüllt.
Geben Sie den Fasewinkel der Schnecke ein.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.