The calculation is used for geometrical and strength designs and worm gearing check. The program solves the following tasks.
The calculations use procedures, algorithms and data from standards ANSI, ISO, DIN, BS and specialized literature.
List of standards: ANSI/AGMA 6022-C93 (Revision of AGMA 341.02), ANSI/AGMA 6034-B92 (Revision of ANSI/AGMA 6034-A87), DIN 3996, DIN 3975-1, DIN 3975-2
User interface.
Download.
Purchase, Price list.
Information on the syntax and control of the calculation can be found in the document "Control, structure and syntax of calculations".
Information on the purpose, use and control of the paragraph "Information on the project" can be found in the document "Information on the project".
Worm (globoid) gearing can transmit high outputs, the common ones being 50 to 100 kW (optimum 0.04kW-120kW, extreme 1000 kW); within one stage, it is able to realize high transmission ratios i = 5 to 100, (up to i=1000 in kinematical transmissions), being of small size, low weight, and compact structure. It features quiet and silent operation and can be designed as a self-locking transmission.
The disadvantage is the large slip in the gearing causing higher friction losses and thereby lower transmission efficiency; the endeavours for improvement require using deficit nonferrous metals for wormgear rims. Gearing production is more demanding and expensive and the service life of such gearing is usually shorter than in rolling gearing.
Worm gearing is used for power transmission in mixers, vertical lathes, vehicles and lifting equipment, textile machines, presses, conveyors, shears, drums, hoists, ship propeller drives, planers, machine tools, cars...
This calculation deals with the most frequently used gearing with cylindrical worm and globoid gear.
Worm gearing is a special case of screw gearing with the angle of axes 90° and a low number of pinion/worm teeth (mostly z1=1-4). Worm gearing types are distinguished by shape as follows:
The formulas given in this article are used in geometry calculation.
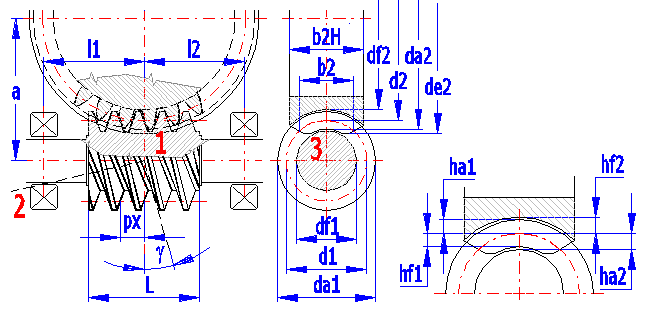
1- Centre-line section (mx,ax,sx,ex) , 2-Normal section (mn,an,sn,en), 3-Worm frontal section
Worm basic profile parameters: m (DP for calculation in inches),a,ha*,c*,rf* Module and pressure angle in the centre-line section are selected for spiral gearing ZA, while module and pressure angle in the normal section are selected for common gearing ZN,ZI,ZK,ZH.
Worm and worm gear parameters: z1, z2, x1=0, x2=x
ZA: df1=d1 - 2 •
(ha* + c*) • mx; df2=d2 - 2 •
(ha* + c* - x) • mx
ZN: df1=d1 - 2 • (ha* +
c*) • mn; df2=d2 - 2
• (ha* + c* - x) • mn
The following formulas are used to calculate the forces occurring in
toothing.
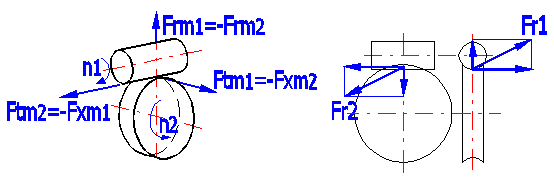
Ftm1=2000 •
T2 / (dm1 •
hges •
z1 / z1) = -Fxm2
Ftm2=2000 •
T2 / dm2 =-Fxm1
Frm1 = -Frm2 = Ftm1
• tan(a)
/ sin(g + r)
Fr1 = (Ftm1^2 + Frm1^2)^0.5
Fr2 = (Ftm2^2 + Frm2^2)^0.5
Total loss of power in worm transmission consists of gearing, bearing and sealing losses. The calculation neglects any losses associated with the lubrication system and transmission cooling. Gearing efficiency is defined as a ratio of the driven and driving members and differs if the worm (index 1) or the wheel (index 2) is the driving member.
Efficiency of gearing: hz = tan(g) / tan(g + rz)
where:
g...pitch angle
r...friction angle r=atan(m)
As the pitch angle increases (with given friction angle), efficiency rises quickly at first to change into a flat curve and drop quickly again (see the Figure).
The curve peak is in the middle of the interval [0; 90-r] and the theoretical maximum efficiency of a worm gearing is then calculated as follows:
hmax = tan(45-r/2) / tan(45+r/2)
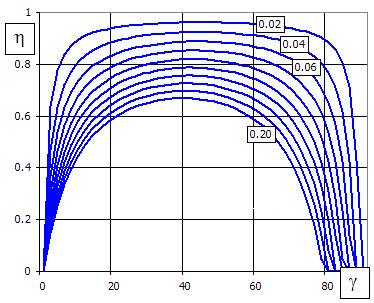
The vertical axis shows gearing efficiency, the horizontal axis shows the pitch angle, and individual curves are for different friction coefficients.
In practice, pitch angles up to 10° and up to 20-25° are used for worms ZA and for common worms ZN, ZI respectively, namely for production reasons. Endeavours after the highest possible efficiency then result in using higher pitch angles, which can be achieved by reducing worm diameter and using multiple worms.
This design is virtually not used in power transmissions.
Efficiency of gearing: hz = P1 / P2 = tan(g - r) / tan(g)
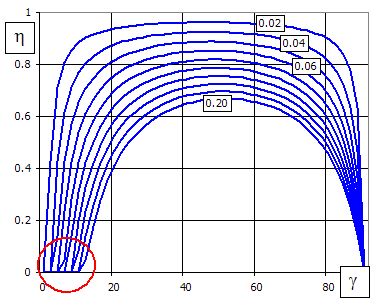
In this case, the point of intersection of the curve with the horizontal axis (red circled), which defines the self-locking limit, is important. It is the moment when gearing cannot be moved using even the highest possible torque acting on the worm gear (this feature is used in lifting mechanisms, for instance). The self-locking limit occurs when the pitch angle equals to the angle of friction.
In practice, the following self-locking features are used as a minimum:
Friction coefficient has the highest effect on transmission efficiency. It depends on a number of parameters (material, surface, lubricant, speed, size). It is calculated using the following formula:
mzm = m0T • YS • YG • YW • YR; line calculation [6.1-6.7]
Total efficiency includes bearing, sealing and no-loads losses and is calculated using the following formula:
hges = Pw2 / (Pw2 + PV), where PV is total power loss; line calculation [6.9-6.15]
Abrasive loss of material occurs during gearing operation, which means that tooth thickness is reduced. This predominantly affects the tooth side made of a material of lower hardness (wheel as a rule). A number of tests were performed recently with different materials, dimensions and oil types, giving the results as shown on the Figure.
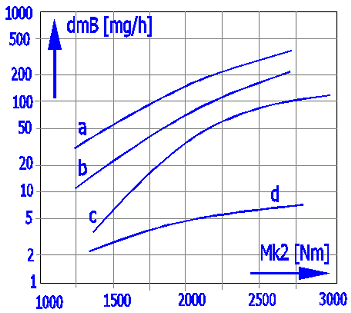
Worm: 16MnCr5E; Wheel: CuSn12Ni-GZ; a=160mm; n1=500; i=20
Curves:
Mineral oil: a) n40=220 [mm2/s]; b)
n40=460 [mm2/s]; c)
n40=680 [mm2/s]
Synthetic oil: d) EO:PO=0:1
As follows from the results, using synthetic oils reduces wear fundamentally. Oil viscosity has an effect in mineral oils only; wear increasing significantly with low viscosity.
Permissible wear of worm gear
dWlimn depends predominantly on
the equipment in which the worm transmission is used. It may be determined by
the maximum backlash in the gearing, for instance. In any case, however,
permissible wear is achieved at the tooth sharpness limit. If no particular
conditions are agreed/determined, the following is considered as a rule:
dWlimn=0.3 • mx •
cos(gm), calculation line
[7.18]
Permissible wear is in the green field, the common value is filled in automatically after activating the ticking box.
SW = dWlimn / dWn ≥ SWmin (SWmin=1.1)
It can be influenced (increased) by choosing lower service life required [2.12], oil of higher grade, higher viscosity [2.7,2.8] and, of course, through the choice of geometrical parameters.
Fatigue cracks occur on the tooth surface through the pulsating load of the tooth side and through the action of sliding friction forces. Oil penetrates into these cracks and hydrostatic forces cause tearing off of surface particles and pitting. The following graph shows pitting occurrence as a function of the load cycles and centre-line distance. The pitting occurrence calculation formula is based on a number of test results and operation experience.
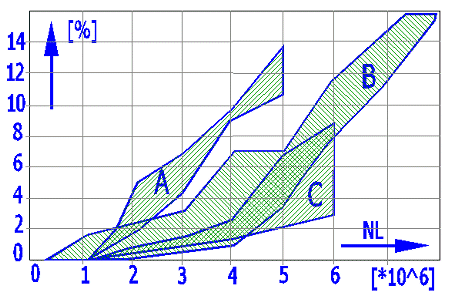
Horizontal axis: load cycle - wheel; vertical axis: [%] of pitting area from tooth side area
Worm: 16MnCr5E; Wheel: CuSn12Ni-GZ; Syntetický olej;
n1=500;
i=20; dHm
= 330 MPa
Curves: A) a=160 [mm]; B) a=100 [mm];
C) a=65 [mm]
The following basic formulas are used to check safety:
![]()
SH = sHG / sHm ≥ SHmin (SHmin=1.0)
It can be influenced (increased) by choosing lower service life required [2.12], oil of higher grade [2.7] and, of course, through the choice of geometrical parameters.
Too great and dynamically changing worm deflection may result in interferences and thereby in increased wear.
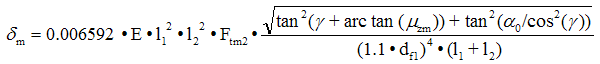
![]()
The value of permissible deflection was achieved from practical experience.
Sd = dlim / dm ≥ Sdmin (Sdmin = 1.0)
If too high stress on the tooth root occurs, gear teeth suffer plastic deformation resulting in a shift in the contact area and subsequent breaking of the tooth. Research studies and tests of tooth root stress were performed for different centre-line distances, transmission ratios, diameter quotients and different materials. The Figure shows test results and values calculated as per DIN 3996.
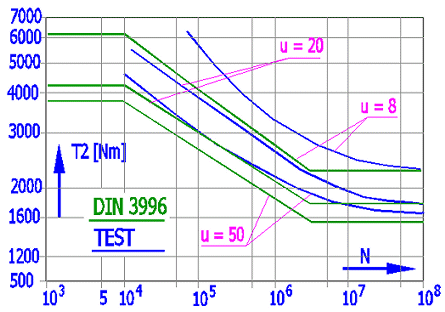
Horizontal axis: load cycle – wheel; vertical axis: output torque
Worm: 16MnCr5E; Wheel: CuSn12Ni-GZ; Synthetic oil; a=120,u=8/20/50.
Green: calculation to DIN, Blue: test result, failure probability 50[%]
The tests show that the output torque moment causing tooth damage reduces with the transmission ratio increase. This moment increases with reduced load cycle. At the same time, the tests show that permanent plastic deformation occurs before tooth breakage in bronze wheels.
tF = Ftm2 / (b2H • mx) • Yeps • YF • Yg
tFG = tFlim • YNL
The value of maximum permissible output to AGMA was used as an input value to calculation to DIN for the purposes of the following graphs.
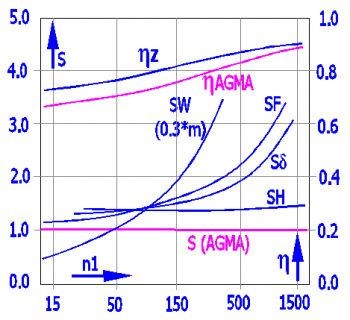
Worm: 16MnCrSEh; Wheel: GZ-CuSn12Ni; polyglycol (EO:PO=0:1); a = 180 mm; u = 50/2; L = 25000 h
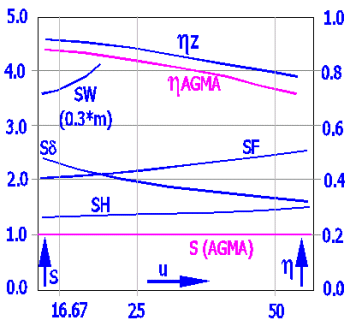
Worm: 16MnCrSEh; Wheel: GZ-CuSn12Ni; polyglycol (EO:PO=0:1); a = 180 mm; n1 = 500 rpm; L = 25000 h
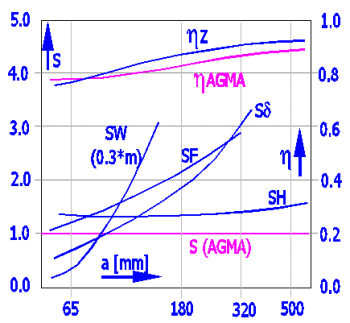
Worm: 16MnCrSEh; Wheel: GZ-CuSn12Ni; polyglycol (EO:PO=0:1); u = 50/2; n1 = 500 rpm; L = 25000 h
When designing a gearbox, one should also consider the heat generated inside the gearbox (efficiency of gearing, friction of bearings, and friction in sealing). This parameter is not so important in spur or bevel but it is in worm gearing. As worm gearing efficiency is lower considerably than that of spur or bevel gearing, considerably more heat is generated in the gearing and has to be removed. Therefore, thermal safety has great importance for a correct design to ensure gearbox function within the permitted temperature range of oil. Thermal design/safety tends to be one of the limiting factors when designing transmissions.
In addition to an approximate formula for heating calculation as per DIN 3996, this calculation also includes a simple temperature analysis. This analysis makes it possible to calculate the heat passing through the gearbox walls and the heat removed by oil cooling. For designs of important transmissions it is in any case recommended to make a detailed thermodynamic analysis, best in connection with pertinent tests.
Two fundamental formulas are used in this temperature analysis, namely:
P = k • A • dT
where:
P..... power losses [kW]
k..... combined heat transfer coefficient (heat transmission, radiation)
[W/m2*K]
A..... gearbox outer surface [m^2]
dT... temperature difference between oil and ambient air temperature [°C]
A number of recommendations can be found in the literature for coefficient k determination. Selected values are provided in the Article [11.12].
Basic area A is given by the calculation as a minimal right parallelepiped free from any projections and ribbing, which comprises the designed gearing. The ribbing effect is then established by means of a coefficient.
P = c • ro • Q • dT
where:
P.....cooler power [kW]
c.....oil specific heat [Ws/Kg/°K]
ro... oil density [kg/dm3]
Q... oil volume [litre/s]
dT.. temperature difference between oil leaving the gearbox and cooled oil
re-entering the gearbox.
Gear transmissions are split into:
Power gearing – The gearing intended predominantly for power transfer and transformation must be designed/checked for strength (e.g. machine drives, industrial gearboxes…).
Non-power gearing – No strength design/check needs to be performed in gearing where the torque moment is minimal given the wheel size (e.g. instrumentation, regulation equipment...).
Any worm gearing design provides considerable liberty in selecting gear diameters and width. Therefore, the calculation makes it possible to create a table of proper solutions to pick from a number of parameters, such as weight, centre-line distance, efficiency, etc.
The result of this procedure is a table of proper solutions of the gearing being designed.
Although the solution table provides correct proposals, it is advisable to optimize and fine-tune some parameters, namely centre-line distance [4.23,4.24] and worm bearing distance [4.16,4.17].
The following procedure is most appropriate in power gearing:
An auxiliary calculation [16.0] can be used for non-power gearing.
No strength parameters need to be addressed and checked when designing a non-power gearing. Therefore, directly select the proper number of teeth and a module [4.8-4.20] and check the dimensions of the gearing being designed.
Enter the basic input parameters for the gearing being designed in this article.
Select the required system of calculation units in the list of options. All values will be recalculated immediately after changing the units.
Select the driven element (worm or gear) in the list of options.
Enter the required power on the worm gear. The common values range from 0.1 to 300kW / 0.14-420HP, in extreme cases up to 1000kW / 1400HP. Using the right push-button, calculate the maximum power the particular worm gearing is able to transmit.
Enter the worm speed. The common worm speed is up to 3000 rpm, while extreme speed may be up to 40000 rpm. Worm gear speed is calculated from the number of teeth of both gears.
It is the calculation result and cannot be entered.
The optimum transmission ratio ranges between 5 and 100. In extreme cases, it may reach up to 300 (1000 in non-power gearing). Transmission ratio is entered in the left entry field using the keyboard. The roll-out menu on the left offers the recommended transmission ratio values; when choosing from this menu, the selected value is added to the left field automatically.
Since the actual transmission ratio is the proportion of the number of teeth of both gears (integers), the actual transmission ratio will mostly differ from the required (entered) one. The value of the “Actual transmission ratio” is shown on the left, while the percentage deviation from the required one is given on the right.
When designing a power transmission, enter additional operational and production input parameters in the article. Try to be as accurate as possible when choosing and entering these parameters as each one of them may have a dramatic effect on the properties of the gearing being designed.
Worm gearing strength is limited by various conditions, namely:
These conditions must be reflected when choosing the worm and gear materials. Hardened and ground worm mating with tin or phosphorus bronze gear is mostly selected.
The basic material is bronze, less frequently being cast iron or brass. Plastic gears are used for lower powers (to absorb shocks and provide lower noise) and non-power gearing. Bronze gears are manufactured as composite for economical reasons (a bronze rim put on a steel or cast-iron wheel). Centrifugal casting is advisable.
The optimum options are tin bronze with high Sn content of 10-12% (excellent friction properties, high resistance to seizure and good running-in), but are too expensive. Their application can only be justified in loaded transmissions and with sliding speed exceeding 10 m/s. Even in these cases, however, there is an effort to replace them by Sn-Ni bronze and other alloys. Bronze with lower Sn content (5-6%) can be used for speed v = 4-10 m/s.
Less expensive bronze free from tin, e.g. aluminium or lead bronze, or brass are suitable for speeds v<4 m/s. They are relatively hard and strong, but are less resistant to seizure and are not so good for running-in. The mating worm, therefore, must have high surface hardness (HRC>45). In gearing with a greater worm gear, a combination of bronze worm and cast-iron gear can be used for economical reasons.
Grey cast iron mated with a steel worm can be used for low outputs, quiet load and low peripheral speed up to 2 m/s.
Carbon or alloyed steel which allows surface heat hardening (hardening to HRC 45-50, cementing and hardening to HRC 56-62, and nitriding) is used for worms. Tooth sides are ground and/or polished. When nitrided, the material need not be ground and polished only. Heat-treated or normalized steel worms are only used for lower outputs and lower peripheral speeds.
Customer’s own material values – If a material which is not specified in the table of materials should be used for gearing, a number of data should be entered about the material. Go to the sheet “Materials”. The first 5 lines in the materials table are reserved for defining the customer’s own materials. Enter the material name in the pertinent column (will be shown in the options menu) and fill in all parameters in the line (white boxes) gradually. After that, go to the “Calculations” sheet, select the newly defined material and continue the calculation.
Select the type of worm. For details on worm types see the theoretical section of the Help.
Setting of these coefficients substantially affects the calculation of safety coefficients. Therefore, try to enter as accurate a specification as possible when selecting the type of loading. Examples of driving machines:
Setting these parameters substantially affects the calculation of safety coefficients. Therefore, try to enter as accurate a specification as possible when selecting the type of loading. Examples of driven machines:
The types of gearing lubrication and gearbox cooling (or oil on pressure lubrication) depend on a number of conditions such as power transmitted, transmission ratio, speed, material, gearbox design, application, etc. The design can be based on worm peripheral speed, but all the conditions must be reflected in the final design.
Oil bath lubrication: 0-4 [m/s] (0-13 [ft/s])
Oil-spray lubrication: 2-10 [m/s] (6-33 [ft/s])
Pressure circulation lubrication: 8 and more [m/s] (25 [ft/s])
Mineral oil can be used for less loaded gears, while synthetic oil is recommended for higher speeds, higher powers transmitted and higher efficiency requirements.
Some advantages of synthetic oils
These advantages are opposed by higher price, possible problems with the plastic or rubber parts, and limited miscibility with mineral oils.
In the menu, oils are ordered by ISO (AGMA) viscosity. By selecting oil from the menu, selected oil parameters are transmitted to corresponding boxes (viscosity at 40 °C, viscosity at 100 °C, specific weight [kg/dm^3]). If oil parameters are known from the manufacturer’s material sheet, enter the parameters in the appropriate boxes [2.9,2.10].
| Bulk temperature [°C] | Sliding speed [m/s] | |||
| Max. working | Starting | < 2.5 | 2.5 ... 5 | >5 |
| 0 - 10 | -10 - 0 | 110 … 130 | 110 … 130 | 110 … 130 |
| 0 - 10 | >0 | 110 … 150 | 110 … 150 | 110 … 150 |
| 10 - 30 | >0 | 200 … 245 | 150 … 200 | 150 … 200 |
| 30 - 55 | >0 | 350 … 510 | 245 … 350 | 200 … 245 |
| 55 - 80 | >0 | 510 … 780 | 350 … 510 | 245 … 350 |
| 80 - 100 | >0 | 900 … 1100 | 510 … 780 | 350 … 510 |
| AGMA no of Gear Oil | ISO Viscosity Grade | |
| R & O | EP | |
| 1 | VG 46 | |
| 2 | 2 EP | VG 68 |
| 3 | 3 EP | VG 100 |
| 4 | 4 EP | VG 150 |
| 5 | 5 EP | VG 220 |
| 6 | 6 EP | VG 320 |
| 7 7comp | 7 EP | VG 460 |
| 8 8comp | 8 EP | VG 680 |
| 8A comp | VG 1000 | |
| 9 | 9 EP | VG 1500 |
Enter the value from the oil manufacturer’s material sheet.
Enter the value from the oil manufacturer’s material sheet.
Enter the roughness value. The following Ra values can be achieved for working methods:
It is proposed based on load irregularity from the driven/driving machine [2.4,2.5]. The value is filled in automatically after activating the ticking box. The KA factor is used to multiply the torque value.
The parameter specifies the desired service life in hours. Orientation values in hours are given in the table.
|
Specification |
Durability |
| Household machines, seldom used devices | 2000 |
| Electric hand tools, machines for short-term runs | 5000 |
| Machines for 8-hour operation | 20000 |
| Machines for 16-hour operation | 40000 |
| Machines for continuous operation | 80000 |
| Machines for continuous operation with log service life | 150000 |
Use lines [2.14-2.17] to enter the requested coefficients of safety. When calculating the table of proper solutions [4.1], only those solutions will be entered in the table which meet the required coefficients of safety. Recommended values are provided on the right of the entry field.
Parameters of the tooth profile can be changed within a wide range and are often dependent on the manufacturing possibilities. The following values are commonly used:
Addendum - Coefficient of the height of the tooth head ha* = 1.0
Unit head clearance ca* = 0.25 (0.2,0.3)
Coefficient of the root radius rf* = 0.38
This is the central article of the whole calculation and the worm gearing geometry design. It is divided into three, closely interrelated parts.
The table of proper solutions is set up as follows: Numbers of worm teeth are entered in the calculation gradually (the range is set in [4.3]); worm diameter quotient q is gradually entered for each value (the range is set in [4.4]); and a minimum module value is searched for every such combination (and/or maximum value DP for inches) which meets the safety coefficients required (selected in [4.2]). After finding all proper solutions, the table is sorted by the parameter set in line [4.5] and the first solution in the table [4.7] is put into the calculation.
Start table calculation pressing the “Run the table” push-button. The calculation process is shown in the dialog.
In this line, tick the safety type which must be fulfilled to include the solution in the table of solutions. Set the coefficients in lines [2.14-2.17]. It is recommended to have the check of all coefficients activated.
In this line, enter the range of worm tooth number z1 for which the table should be solved. Usually z1=1~4 (higher number of worm teeth z1 for higher transmission ratio) is used.
The range of permissible values is z1=1~12, the first value being lower than or equal to the second one.
In this line, enter the range of diameter quotient q for which the table should be solved. Usually q=8-16 (higher value q for smaller module).
The range of permissible values is q=6~25, the first value being lower than or equal to the second one.
Choose by which column the table has to be sorted.
By selecting a solution from the table, the solution parameters are transferred into the calculation. The small push-button "<" on the right will transfer the values from the actual table line into the calculation.
The table includes the following parameters:
In this section, one can define directly all important worm gearing parameters which influence and define its geometry. The description and importance of individual parameters are specified for each of them.
Enter the number of teeth of worm. The value commonly used ranges from 1 to 4, in special cases up to 12. It is recommended to select the proper number of teeth from the table of solutions [4.6] on the basis of your optimization requirements (e.g. weight, efficiency, centre-line distance ...). In any case, it is advisable to consult manufacturing possibilities with the technologist.
The number of worm gear teeth is calculated on the basis of the required transmission ratio. The number of gear teeth must acquire a certain minimum value; otherwise, tooth undercut would occur. If this is the case, the minimum value is shown in brackets and the box text is shown in red.
Axial pressure angle is entered for the ZA type worm, while normal pressure angle is entered for other types (ZN,ZI,ZK,ZH). Pressure angle is selected from 15º to 30º.
The value of 20º is commonly used. Pressure angle can be selected in dependence on the requirements for the equipment being designed. Greater pressure angle results in higher safety against fatigue break (SF) and lower danger of gear tooth undercut. On the other hand, greater pressure angle reduces the number of engaged teeth, increases bearing load and the worm deflection load (greater worm deflection). Pressure angle can also be selected in dependence on pitch angle [4.13], the greater being the pressure angle, the greater pitch angle is chosen.
Minimum number of gear teeth in dependence on pressure angle at zero gearing correction (table in Help).
| Pressure angle [º] | Min. z2/NG |
| 14.5 | 40 |
| 17.5 | 27 |
| 20 | 21 |
| 22.5 | 17 |
| 25 | 14 |
| 27.5 | 12 |
| 30 | 10 |
Worm diameter d1 is virtually arbitrary with the chosen number of worm teeth z1 and the known module value (mx or mn), unless a certain value of pitch angle g is required. In the effort towards the least possible number of screw cutters for manufacturing work gears, the manufacturers recommend choosing d1=q•m, where q is the coefficient depending on the size of standardized module m. In consideration of worm rigidity in bending, greater values q are assigned to lower values m.
| m | 2 | 2.5 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | 16 | 20 | 25 |
| q | 16 | 12 | 12 | 9 | 9 | 9 | 8 | 8 | 8 | 8 | 8 | 6 |
| 14 | 10 | 10 | 10 | 9 | 10 | 10 | ||||||
| 12 | 12 | 12 | 10 | |||||||||
| 14 | 14 | 14 | 12 |
If you require entering a precise worm diameter value, activate the entry field by ticking the selection push-button. The recommended approximate value d1 in dependence on the module and on the number of worm teeth is given on the right of the entry field.
Pitch angle is one of the key parameters of worm gearing closely related to worm dimensions and transmission efficiency. Efficiency grows with increasing pitch angle (for detailed information see the efficiency section).
The important pitch angle is at the self-locking limit (friction angle [6.8] is equal to pitch angle). This angle is filled in after pressing the "<=SL" push-button on the right.
6º-40º in worms manufactured from one piece
do 17º in worms put on a shaft
Select pitch direction. It only has an effect on force orientation and sense of rotation. Unless the drive kinematics require otherwise, the worm has the right sense of rotation.
Module (DP) is the key parameter which affects the gearing size and, thereby, pertinent safety coefficients. The following entries are required in dependence on the selected calculation units [1.1]:
Gearing module is required, axial mx for ZA worm type and normal mn for other types (ZN,ZI,ZK,ZH).
The DP value (Diametral Pitch) is required.
The table value can be selected from the options menu on the right.
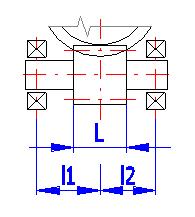
Bearing distance from worm centre (see the Figure) has a direct impact on
worm deflection and thus on worm deflection safety. In the line [4.17] enter the
distance of the left and right bearing from the gear centre as percentage of
worm gear outer diameter. This method of selection is used automatically when
calculating the table of proper solutions [4.6]. If you require entering a
precise value, clear the ticking box on the line [4.18] and enter the precise
value.
Worm face width is proposed automatically on the basis of the module and the number of teeth. If you want to enter your own value, clear the ticking box on the right.
Worm face width is proposed automatically on the basis of worm diameter. If you want to enter your own value, clear the ticking box on the right.
In principle, the worm is manufactured without any addendum modification. Worm gear only is modified, the main reason for using addendum modification (manufacturing tool shifting) being to achieve required (standardized) centre-line distance. The use of addendum modification to eliminate tooth root undercut or to improve tooth bending strength is less frequent.
The minimum value of the addendum modification coefficient to prevent tooth root undercut is given on the right of the input box. If the actual value is lower, the value is shown in red. The minimum addendum modification coefficient depends on the number of gear teeth [4.9] and on the pressure angle [4.10].
A worm gear design with given axis distance is the most frequent task. The following procedure is recommended for designing:
Axis distance can be influenced by a number of parameters. The following can be used in this calculation:
For every method, the range of possible parameter change is specified in brackets "<>" and the range of possible change in axis distance is specified in parentheses "( )".
The first box shows the weight of the complete gearbox (the sum of weights of gear wheels, shafts and gearbox body). The second box provides the weight of the worm and gears including shafts. Cast iron is considered as material for gearbox weight calculation.
The first box shows the total efficiency of the actually designed gearing, while the right one shows the maximum theoretically possible efficiency for the actual conditions (lubrication, materials, bearings, etc.).
Total efficiency is affected most by pitch angle [4.13], when higher pitch angle results in higher efficiency.
This article provides a well-arranged list of all basic dimensional parameters of gearing. Formulas used, figures and other information are specified in the theoretical section of the Help.
It is the greatest diameter of worm gear, while the approximate recommended value as per DIN 3975 is: de2=da2+mx, which has been pre-set. The minimum and maximum values are provided in the green box on the right.
If a specific value has to be entered, clear the ticking box in this line.
This article provides calculation of gearing efficiency and all other relating parameters. Formulas used, figures and other information are specified in the theoretical section of the Help.
Bearing losses are one of the parameters having an impact on efficiency. This value depends on bearing type and supporting method. Identify the worm shaft supporting method in the options menu.
This article shows wear safety calculation. More detailed information is available in the theoretical section of the Help.
Permissible wear of tooth gear dWlimn depends predominantly on the equipment in which the worm gear is used. It may be determined by maximum clearance in toothing, for instance. In any case, however, permissible wear at the tooth sharpness point will be achieved. Unless particular conditions have been determined/set, the following is considered as a rule
dWlim=0.3 • mx • cos(gm)
Permissible wear is shown in the green box, while the actual value appears automatically after activating the ticking box.
It can be controlled (increased) by choosing lower required service time [2.12], oil of higher grade, higher viscosity [2.7,2.8] and, of course, selecting geometrical parameters.
This article provides the pitting safety calculation. More detailed information is available in the theoretical section of Help.
The article provides the calculation of worm deflection and reactions in supports (bearing loading). More detailed information is available in the theoretical section of Help.
This article provides the calculation of root-strength of teeth. More detailed information is available in the theoretical section of Help
Enter the thickness of gear rim. The minimum recommended value is added automatically so that the rim thickness coefficient is YK=1.0
Higher life factor is conditioned by higher plastic deformations only acceptable for gearing with lower accuracy grade. If higher reliability is required, it is advisable to set life factor to YNL=1.0. If the ticking box is crossed, the value based on material used, number of load cycles and accuracy grade selected is filled in automatically.
This article provides the tools for calculation and check of gearbox energy balance. Since worm gear efficiency is substantially lower than that of spur or bevel gearing, considerably more heat which has to be removed is generated in the gearing. Therefore, thermal safety is of great importance for correct design, which would ensure gearbox function within the permissible oil temperature range.
The first section provides thermal safety calculation to DIN 3996, method C, while the other includes a worm gearing thermal analysis. More detailed information is available in the theoretical section of Help.
Enter ambient air temperature, usually 20°C [68°F].
The usual maximum temperatures are for:
Temperature appears automatically according to the oil type selected. If you want to enter your specific value, clear the ticking box.
Select whether a fan is attached to the worm shaft or the gearbox has no fan.
According to DIN 3996, it is possible to use an approximate formula to calculate the temperature of a well-ribbed gearbox for cast-iron gears with centre-line distance 63-400 [mm], worm speed 60-3000 [rpm] and transmission ratio 10-40. A deviation of ± 10°K from the actual value should be taken into account.
The approximate formula result shows gearbox temperature [11.6] and thermal safety [11.7], which should be higher than 1.1.
This section enables making a simple thermal analysis of a gearbox. Most input parameters are estimated on the basis of size, power transmitted, design type and others. But more precise values can also be used, obtained from measurement on a similar gearbox or from the professional literature, for instance. Clear the ticking box in the pertinent line to enter a specific value of a required parameter.
It is proposed on the basis of oil used so as to achieve thermal safety coefficient 1.1.
Select the type of gearbox surface (design) in the options menu. The parameter has an impact on surface estimate [11.11].
Surface area is achieved by an approximate calculation based on gearing dimensions. It is advisable to use a suitable output from the CAD 3D model for precise calculation (check).
Heat transfer (transmission, radiation) coefficient depends on the gearbox operation environment (ventilation, room size), gearbox size, ribbing, number of worm speed, temperature, etc. The use of a fan can triple the coefficient. Any precise calculation of the coefficient is therefore difficult and requires a thorough analysis. Values from 5 [W/m2*K] to 50 [W/m2*K] were measured in practice. If the ticking box is crossed, an approximate value estimated based on gearbox speed, size and design is added automatically.
Basic values for box without fan:
- Small unventilated rooms ...8-12 [W/m2*K]
- Well ventilated rooms ...14-20 [W/m2*K]
Fan effect: The use of a fan may increase the coefficient by up to
100%
Size effect: Small gearboxes may have the coefficient up to 50% higher
than big ones
Temperature effect: The coefficient may increase by up to 15% with the
difference of ambient temperature and oil temperature increasing
Speed effect: The coefficient increases with worm speed increasing
In gearboxes where the loss heat is higher (higher power, lower efficiency), natural cooling is often insufficient and additional oil cooling must be used in the form of an external oil cooler or a cooling worm in the gearbox. This line shows the loss power necessary to achieve the required temperature [11.9]. If additional cooling is not required, the value is zero.
If oil-spray lubrication is selected [2.6], the volume of oil supplied by the pump can be proposed in this section.
Specify in this line whether or not an oil cooler is used. Oil cooler application has an effect on the temperature difference of the lubrication oil.
It is the difference of temperatures between oil drawn by the pump and sprayed oil.
The usual values are as follows:
The value for lubrication oil is pre-set at 1900 Ws/Kg/°K [0.454 BTU/lb/°F]
Such oil spray volume which will guarantee gear cooling to the required temperature [11.8] is proposed on the basis of entered parameters [11.8-11.15].
It should be lower than the extreme value [11.2]
The value should be higher than 1.1
This article provides a calculation of dimensions as per AGMA 6022-C93. Since the design of worm gearing allows considerable liberty, some dimensional parameters to DIN and to AGMA may differ.
A strength calculation (check) according to AGMA is given here to have the full picture. In comparison with the calculation to DIN, the one to AGMA is much simpler, comprising less input parameters. This, of course, has an impact on calculation accuracy. It is therefore recommended to use the check to DIN, which is more precise and describes the worm gear behaviour better. Comparison of both is in the theoretical section.
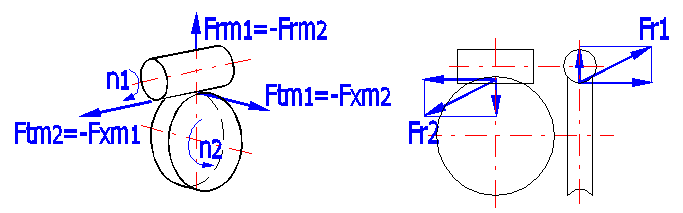
Forces are generated in loaded gearing and transmitted to the machine structure. The knowledge of these forces is quite crucial for proper dimensioning. Force orientation is shown on the figure and force magnitudes are specified in this article [14.1-14.6].
This article provides the material characteristics of pinion and gear.
This article provides the calculation of parameters necessary to achieve the required precise centre-line distance. Enter the number of worm teeth and the number of worm gear teeth in the line [16.1]. Enter the required centre-line distance in the line [16.2] and press the "Run the calculation" push-button. The calculation may take several seconds and the table of proper solutions in the line [16.4] is filled in after it. After selecting a suitable variant from the table, the parameters (z1,z2,modul,q,x) are transferred to the main calculation.
Project notes: The calculation does not take the strength parameters of the worm gearing into account.
This article offers shaft diameters (steel) corresponding to required load (power transmitted, speed). These values are approximate only and a more precise calculation should be used for the final design.
Auxiliary calculations are available in this article. Use the same units when entering values as in the main calculation. Transfer the entered and calculated values to the main calculation by pressing the "OK" push-button.
Information on options of 2D and 3D graphic outputs and information on cooperation with 2D and 3D CAD systems can be found in the document "Graphic output, CAD systems".
Additions – This calculation:
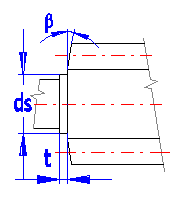
Enter the values according to the Figure. If the ticking box is crossed, the values are entered automatically.
Enter the angle of worm shrink.
Information on setting of calculation parameters and setting of the language can be found in the document "Setting calculations, change the language".
General information on how to modify and extend calculation workbooks is mentioned in the document "Workbook (calculation) modifications".