Die Berechnung ist für den geometrischen Entwurf und die komplexe Kontrolle der Wellen bestimmt.
Das Programm löst folgende Aufgaben.
Einfache Definition der abgesetzten Wellen, einschließlich der hohlen.
Eine Möglichkeit der Definition von Einstichen, Absätzen, Nuten und Berechnung der entsprechenden Koeffizienten der Spannungskonzentration.
Einfache Definition der räumlichen Wellenbelastung.
Berechnung der Reaktionskräfte, des Kraftflusses, der Momente, der Spannung, der Durchbiegung und Verdrehung der Welle und Weiteres.
Berechnung der kritischen Drehzahl und der Sicherheitskoeffizienten.
Unterstützung der 2D und 3D CAD-Systeme.
In der Berechnung sind Daten, Verfahren, Algorithmen und Angaben aus der Fachliteratur und Normen AGMA, ISO, DIN und BS benutzt. Normenliste (DIN 743)
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Die Wellen verwendet man in den meisten Fällen zur Übertragung der Rotationsbewegung und der Drehmomente. Sie sind ein übliches Tragelement der Zahnräder, Riemenscheiben, Kupplungen, Rollen usw. und sind mit einer räumlichen Biegung, Drehmomenten und Achskräften belastet. Ein überwiegender Teil der Wellen ist durch Absätze, Einstiche, Nuten und Bohrungen geformt, die unerwünschte Spannungskonzentrationen hervorrufen. Beim Entwurf ist daher zweckmäßig, folgende Kriterien in die Berechnung einzubeziehen und zu kontrollieren:
Beim Entwurf und der Kontrolle empfehlen wir das folgende Verfahren einzuhalten.
In diesem Absatz kann der Wellendurchmesser auf Grund der übertragenen Leistung, Drehzahl und des Belastungsmodus vorläufig entworfen werden. Dieser Wert wird dann beim Entwurf der tatsächlichen Wellenform als eine Ausgangsform (Orientierung ) verwendet.
In einer Auswahlliste das benötigte System der Berechnungseinheiten wählen. Beim Umschalten der Einheiten werden sofort alle Eingangswerte umgerechnet.
Leistung eingeben, die durch die Welle zu übertragen ist.
Wellendrehzahl eingeben.
Aus der übertragenen Leistung und Drehzahl ist ein Drehmoment gewonnen, der für den vorläufigen Entwurf des Durchmessers maßgebend ist.
Den entworfenen minimalen Durchmesser der Welle als Ausgangsinformation beim Entwurf der tatsächlichen Form und Maße der Welle verwenden, die von Ihnen in folgenden Abschnitten zu kontrollieren ist.
Zwecks eines vorläufigen Entwurfs eine der 3 Möglichkeiten aus der Auswahlliste verwenden.
Zwecks eines vorläufigen Entwurfs eine der 3 Möglichkeiten aus der Auswahlliste verwenden. (A- Werkstoff von niedrigster Qualität , C- hochwertiger Werkstoff ).
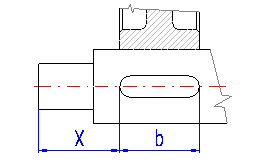
In diesem Abschnitt sind die Wellenform und Positionierung der Auflagerungen (der Lager) zu definieren. Eine Welle kann von Ihnen aus höchstens 10 Zylinder- oder Kegelteilen definiert werden, die auch hohl sein dürfen. Für Übergänge zwischen einzelnen Zylinderteilen ist auch ein Abrundungshalbmesser zu definieren, der die Spannungsberechnung bei einer Festigkeitskontrolle der Welle beeinflusst. Abmessungen der Welle in der Tabelle [2.2] nacheinander eingeben und auf der Abbildung die Form der entworfenen Welle überwachen.
Der Schalter bestimmt, ob die ganze Fläche des Fensters für die Darstellung der Welle ausgenutzt ist (die Welle ist optisch verformt) oder der gleiche Maßstab für das Breit- und Längenmaß benutzt ist.
Die Tabelle für die Wellendefinition enthält zehn Spalten für höchstens zehn zylindrische (kegelförmige) Wellenabschnitte und Zeilen, in denen die Maßparameter des entsprechenden Wellenabschnittes einzugeben sind. Richten Sie sich nach der schematischen Abbildung.
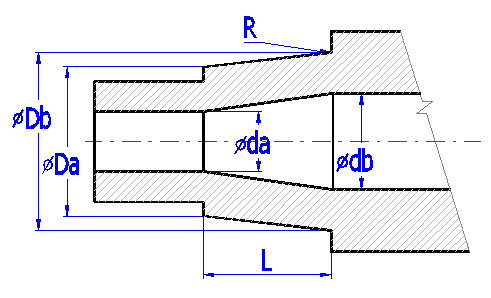
Untereinander folgend:
| Anfang | Anfängliche Koordinaten des zylindrischen Wellenteiles vom linken Wellenrand. |
| L | Länge des Wellenteiles. |
| Da | Außendurchmesser links |
| Db | Außendurchmesser rechts |
| da | Innendurchmesser links |
| db | Innendurchmesser rechts |
| R | Abrundung zwischen zylindrischen Abschnitten. (ist für den rechten Seitenrand definiert, siehe Beispiel |
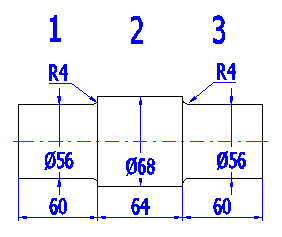
| 1 | 2 | 3 | |
| Start | 0 | 60 | 124 |
| L | 60 | 64 | 60 |
| Da | 56 | 68 | 56 |
| Db | 56 | 68 | 56 |
| Da | 0 | 0 | 0 |
| Db | 0 | 0 | 0 |
| R | 4 | 4 |
Der Parameter gibt die Gesamtlänge der Welle an.
Durch den Schalter rechts stellen Sie ein, welche Stütze (Lagerung) fest und welche verschiebbar ist. Die Einstellung beeinflusst die Spannungsberechnung bei einer Axialkraft. Die Lage und Art der Stütze ist in der Abbildung der Welle als ein rotes Dreieck dargestellt.
Die Qualität der Wellenoberfläche kann wesentlich die Ermüdungsfestigkeit beeinflussen, besonders bei härteren Werkstoffen. In der Auswahlliste entsprechende Oberfläche (Bearbeitungsart) wählen. In der Klammern befindet sich die entsprechende Rauheit Ra in Einheiten [mikrometr/mikroinch].
Bei einer dynamischen Belastung der Welle oder bei Verwendung von spröden Werkstoffen kommt es zur unerwünschten Spannungskonzentration an Stellen der Formänderungen der Welle (Einstiche, Nuten, Schmieröffnungen, Abrundungen zwischen Abschnitten...). Meistens ist die höchste Spannung gerade auf diesen Stellen. Empfehlenswert ist es deshalb, diesen Einfluss bei der dynamischen Beanspruchung der Wellen in die Berechnung einzubeziehen und die Kerben in diesem Absatz zu definieren.
In diesem Absatz ist der Wert der Zerreißgrenze des benutzen Materials für die Bestimmung des Einkerbkoeffizienten b. Wenn das Anhakfeld angehakt ist, ist ein Wert gemäß dem ausgewählten Werkstoff der Welle [6.2] verwendet.
Der Empfindlichkeitskoeffizient q ist für die Berechnung der Kerbempfindlichkeitszahl b aus dem Koeffizienten der Kerbform und nach der Formel benutzt:
![]()
Bei dem angehakten Feld [3.1] ist der Empfindlichkeitskoeffizient verwendet nach dem ausgewählten Werkstoff der Welle [6.1].
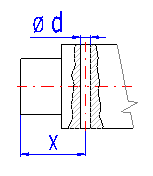
Wenn die entworfene Welle eine Durchgangsbohrung enthält (Durchgangsbohrungen), in die Tabelle Parameter gemäß der Abbildung A eingeben. In der schematischen Abbildung ist die Bohrungposition durch eine rote Linie gekennzeichnet.
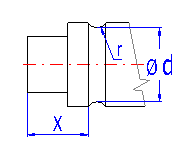
Wenn die Welle mit einem oder mehreren Einstichen versehen ist, ihre Parameter in die Tabelle gemäß Abbildung B eingeben. In der schematischen Abbildung ist der Einstich durch ein grünes Rechteck gekennzeichnet.
Die Wellen enthalten gewöhnlich eine ganze Menge von weiteren Kerben - der potentiellen Spannungskonzentratoren. Manche übliche Typen (die Federnute, Nutenwellen und das Aufpressen) sind in der Auswahlliste angeführt. Die Stelle und den Wirkungsbereich nach der Abbildung C einstellen. Die allgemeine Kerbe ist in der schematischen Abbildung durch eine blaue Maßzahl markiert.
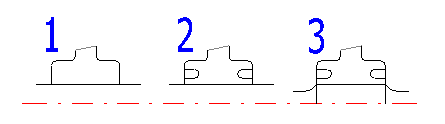
Den Typ der aufgepresssten Verbindung nach der Abbildung wählen.
Die Tabelle enthält Kerbkoeffizienten in der Abrundungsstelle zwischen einzelnen Wellenabschnitten b .
Für die Definition der Belastung gelten folgende Regeln:
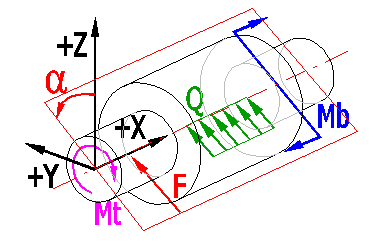
Belastung in der "Definitionsebene"
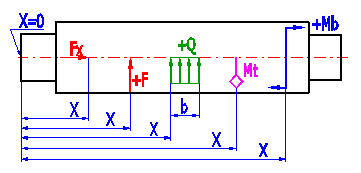
In der Tabelle der belastenden Kräfte maximale Höchstkräfte eingeben. Den dynamischen Charakter der belastenden Kräfte im Absatz [6] spezifizieren. Die Bedeutung der eingegebenen Parameter ist wie folgt:
| X | Der Angriffspunkt der Kraft vom Wellenanfang gemessen (Punkt 0) |
| Fx | Axialkraft (in der Welllenachse wirkende Kraft) |
| F | Senkrecht auf die Wellenachse wirkende Kraft (liegt in der "Definitionsebene" ) |
| alfa | Winkel zwischen "Haupt-" und "Definitionsebene" (für die Kraft F) |
| Mt | Drehmoment |
| Mb | Biegemoment (liegt in der "Definitionsebene ") |
| alfa | Winkel zwischen der "Haupt-" und "Definitionsebene" (für Moment Mb) |
| Q | Stetige Belastung in "liegt in der Definitionsebene " |
| b | Länge der Wirkungsstätte der stetigen Belastung |
| alfa |
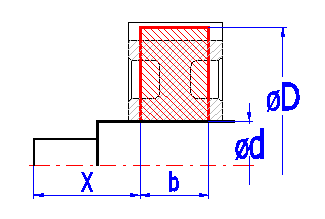
Für die Berechnung der kritischen Drehzahl der Welle [7.13] sind alle materiellen Scheiben zu definieren, die mit der Welle fest verbunden sind. In die Tabelle kann direkt das Gesamtgewicht der Scheibe eingegeben werden und deren Stellung auf der Welle, oder eine Hilfsberechnung verwendet werden, die das Gesamtgewicht aus deren Breite und dem äußeren und inneren Durchmesser errechnet.
Wenn die Orientierung der Welle in der Maschine waagerecht ist und umlaufende Massen die Wellendurchbiegung beeinflussen, den Umschalter auf "Ja" einstellen. Wenn die Orientierung der Welle senkrecht ist, und umlaufende Massen die Wellendurchbiegung nicht beeinflussen, den Umschalter auf "Nein" einstellen (in diesem Fall wird auch die zusätzliche Axialbelastung der Welle nicht berücksichtigt).
In der Tabelle können höchstens 5 zusätzliche materielle mit der Welle fest verbundenen Scheiben definiert werden. Wenn der Umschalter am Ende der Zeile eingeschaltet ist, werden die für die Berechnung des Gewichtes die Abmessungen der Scheibe definierenden Werte benutzt. Wenn der Umschalter ausgeschaltet ist, wird das in der letzten Spalte eingegebene Gesamtgewicht verwendet, in der Breite "b" stetig zerlegt.
Bedeutung der Spalten:
| X | Die am Anfang gemessene Koordinate des linken Randpunktes der materiellen Scheibe. |
| D | Außendurchmesser der materiellen Scheibe |
| d | Innendurchmesser der materiellen Scheibe. |
| b | Breite der materiellen Scheibe |
| Ro | Spezifisches Gewicht des Scheibenwerkstoffes |
| m | Gewicht der Scheibe |
In diesen Absatz Werkstoff und Beanspruchungsart der Welle eingeben. Der Werkstoff der Welle kann aus der Werkstoffliste ausgewählt werden (die Festigkeitswerte des Werkstoffs sind aus der Zugfestigkeit und aus dem Werkstofftyp abgeleitet) oder es lassen sich eigene Festigkeits- und Werkstoffwerte eingeben.
Aus der Auswahlliste ist der Werkstofftyp auszuwählen, aus dem die Welle herzustellen ist. In der Klammer ist der Festigkeitsbereich in [MPa/psi] angeführt. Aus der Auswahlliste rechts ist die benötigte Zugfestigkeit auszuwählen oder direkt den Wert aus der Zeile [6.2] einzugeben. Wenn das Anhakfeld rechts von der Zugfestigkeit angehakt ist, sind aus der Zugfestigkeitsgrenze andere Festigkeitsparameter ausgerechnet. Diese Werte sind dann in entsprechenden Eingangsfeldern ergänzt. Bei der Typenauswahl sind auch weitere Werkstoffwerte ausgefüllt und zwar das spezifische Gewicht und das Elastizitäts- und Schubelastizitätsmodul.
Die Werkstoffparameter sind für folgende Berechnungen nötig:
| Parameter | Berechnung |
| Fließgrenze | Berechnung des statischen Sicherheitsfaktors |
| Dauerfestigkeit | Berechnung des dynamischen Sicherheitsfaktors |
| Spezifisches Gewicht | Biegespannung, Durchbiegung, kritische Drehzahl |
| Zugelastizitätsmodul | Durchbiegung der Welle |
| Schubelastizitätsmodul | Verdrehung der Welle |
Wenn die Welle durch Eigengewicht biegungsbelastet ist, (horizontal gelagerte Welle), ist der Wert "Ja" zu wählen.
Die Sicherheitskoeffizienten werden der Wellenlänge nach berechnet. Wenn der Sicherheitskoeffizient den eingestellten Wert überschreitet, wird der eingestellte Wert verwendet. Das erlaubt eine Vergrößerung der Diagramme (Zoom) im Bereich eines niedrigen Sicherheitskoeffizienten, was für die Beurteilung des Entwurfes von Wichtigkeit ist.
Der Beanspruchungskoeffizient und0 ist für die Berechnung der reduzierten Spannung (Vergleichspannung) zu verwenden. Der voreingestellte Wert geht aus dem Typ der dynamischen Wellenbelastung aus. Wenn Sie Ihren eigenen Wert eingeben wollen, haken Sie das Anhakfeld an.
Zur Berechnung wird üblich die Nennbelastung verwendet. Der Koeffizient der Maximalbelastung deckt die Differenz zwischen Nenn- und Spitzenbelastung. Für jeden Belastungstyp kann dieser Koeffizient einzeln eingegeben werden.
Der Anlaufsdrehmoment eines Elektromotors ist 150% des Nenndrehmomentes. In diesem Fall ist der Koeffizient der Maximaltorsionsbelastung [6.23] = 1.5.
Vier Auswahllisten erlauben den Typ der Belastung zu definieren, die auf die Welle einwirkt. Einer Vereinfachung wegen wird die Welle für folgende Belastungstypen berechnet.
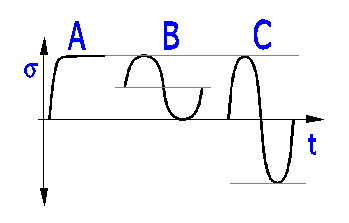
Belastung durch einen Biegemoment - ruhend
Belastung durch eine Schubkraft-ruhend
Belastung durch einen Drehmoment - Schwellend
Belastung durch Zugkraft - ruhend
Belastung durch einen Biegemoment - wechselnd
Belastung durch eine Schubkraft-wechselnd
Belastung durch einen Drehmoment - Schwellend
Belastung durch eine Zugkraft - ruhend
Bei der dynamischen Wellenkontrolle kann ein Einfluss einbezogen werden von der:
Wenn die Welle dynamisch beansprucht wird (wechselnde oder schwellende Belastung oder eine 1000-fach überschreitende Schwingungszahl), dann ist es empfehlenswert, alle Einflüsse einzubeziehen.
In diesem Absatz sind grundlegende Berechnungsergebnisse angeführt, die eine gänzliche Übersicht über die Festigkeits- und Funktionskontrolle dem Entwurf unterliegenden Welle bieten. Im linken Teil sind die Minimum-, Maximum- und ausgewählten Werte angeführt, in dem rechten ein Universaldiagramm, durch das eine beliebige berechnete Kurve dargestellt werden kann. Im unteren Teil dieses Absatzes befindet sich eine Tabelle, wo genaue Werte einer ausgewählten Kurve in ausgewählten Wellenpunkten dargestellt werden können.
Die Größe der ersten und zweiten Auflagerreaktionskraft in der Richtung der X- (Wellenachse), Y- und Z-Achse und gesamte Radialreaktionskraft (S y+z).
Die Maximaldurchbiegung ist ein wichtiger Parameter zur Beurteilung der Wellenfunktionsfähigkeit. Sein erlaubter Maximalwert hängt vom Wellentyp und der Funktion und Konstruktionsspezifizierung ab. Für seine Größe (eine Welle mit einem Zahnrad) sind folgende Empfehlungen gültig:
Auf der Stelle des aufliegenden Zahnrades
oder die empfohlene Maximaldurchbiegung (nicht in der Auflagerungestelle der Räder) ist für:
Diese hängt von der Konstruktion und dem Belastungstyp ab. Der empfohlene Maximalwert j = 0.25° pro Meter Wellenlänge (j = 0.075° pro Fuß Wellenlänge). Im Falle eines sanften Eingriffs, kann der gleichbleibende Drehmoment wesentlich höher sein.
Die Drehung der Welle in der Auflagerungsstelle des Zahnrades sollte nicht einen Wert von 0.05° bis 0.12° (3' - 7')überschreiten.
Die Drehung auf dem Standort des Lagers ist von dem Typ und der inneren Bauart des Lagers abhängig. Allgemein gilt:
| Maximaldrehung [°] | Lagertyp |
| 0.1 | Einreihige Kugellager |
| 3 | Zweireihige Kippkugellager |
| 0.1 | Einreihige Zylinderrollenlager |
| 0.03 | Andere Zylinderrollenlager |
| 1.5 | zweireihiges Pendelrollenlager |
| 0.03 | Einreihiges Kegelrollenlager |
| 2 | Axial-Pendelrollenlager |
| 0.05 | Gleitlager (b/d < 1) |
Es sind Maximalwerte der einzelnen Spannungskomponenten. Maßgebend für den Entwurf sollte jedoch der Sicherheitskoeffizient sein.
1.2 bis 2.2 - Ausreichend verformbare Werkstoffe.
2.0 bis 3.0 - Schmiedestücke, spröde Werkstoffe (hochlegierte Stähle, Gußeisen von hoher Festigkeit)
2.5 bis 3.5 - Schmiedestücke, spröde Werkstoffe (hochlegierte Stahle, Gußeisen von hoher Festigkeit)
Für die Berechnung der kritischen Drehzahl ist wichtig, alle umlaufenden mit der Welle [5] fest verbundenen Massen einzubeziehen. Die kritische Drehzahl wird mit der Rayleigh-Methode berechnet (Biegungsschwingungen).
Die Wellendrehzahl sollte sein:
kleiner als 0.8 * kritische Drehzahl - unterkritischer Betrieb
größer als 1.25 * kritische Drehzahl - überkritischer Betrieb
Wenn die Welle im Bereich der überkritischen Drehzahl arbeitet, ist es notwendig, den Bereich der kritischen Drehzahl möglichst schnell zu übergehen, sowohl beim Anlauf (Leistungsüberschuss) als auch beim Auslauf (manchmal ist Bremsen nötig).
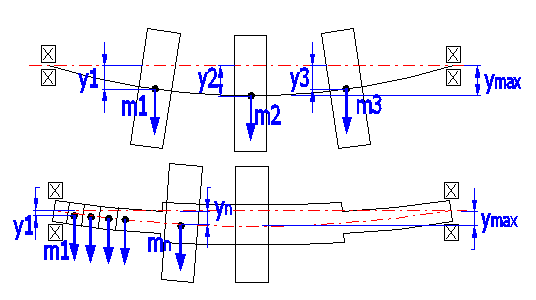
Verwendete Formeln:
Kritische Drehzahl.
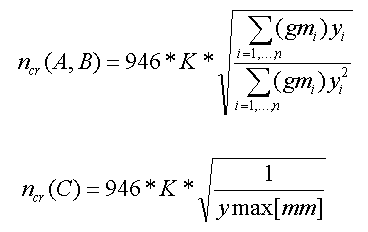
wo:
mi = die i-te rotierende auf der Welle angebrachte Masse.
yi = die statische Durchbiegung unter der i-ten auf der Welle
angebrachten Masse.
g = die Gravitationskonstante.
K = der Faktor des Wellensitzes (weil die kritische Drehzahl außer der
Wellensteifigkeit und Wellendurchbiegung auch von dem Sitz abhängt, ist es
möglich, für die Praxis folgende Faktoren geltend zu machen).
In der Berechnung sind drei Rechenergebnisse angeführt:
In den Auswahllisten wählen Sie die Parameter aus, für die Sie sich interessieren und zum Feststellen genauer Werte an einer bestimmten Wellenstelle. Die Werte können Sie in bis acht Kontrollstellen ermitteln. Deren Koordinaten in die Zeile [7.16] eingeben.
In Auswahllisten die Parameter einstellen, deren Diagramm Sie darzustellen wünschen . Schnelle Bewegung durch alle Diagramme durch Schiebebalkenbewegung durchführen. Für die blaue Kurve ist die Wertachse links angeordnet, für die grüne rechts.
Absätze 8-12 enthalten Diagramme von ausgewählten Werten. In Absätzen 8,9 und 10 lassen sich Darstellungen der Werte in der Ebene XZ, in der Ebene XY, die Wertsumme und der Winkel zwischen der Ebene XZ und dem Vektor des Ergebniswertes (Summe XZ und XY) ein- und ausschalten. Einschalten / Ausschalten des Diagramms durch Anhaken / Abhaken des Anhaktastfeldes durchführen.
Die Informationen über die Möglichkeiten der 2D- und 3D-graphischen Ausgabe und die Informationen über das Zusammenwirken mit den 2D- und 3D CAD-Systemen finden Sie im Dokument "Grafische Ausgabe, CAD - Systeme".
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Für Berechnungen der Reaktionskräfte, Verformungen und Spannungen sind Standardverfahren und Standardformeln verwendet.
Weil eine Menge von Theorien und Verfahren auf dem Gebiet der Berechnungen der Kerbwirkungen und Sicherheitskoeffizienten in der Literatur angeführt sind, geben wir die grundlegenden in der Berechnung verwendeten Formeln an.
![]()
de - Biegespannung.
dg - Zugspannung (Druckspannung).
de -
Torsionsspannung.
ts - Spannung in der Scherung.
a0 - Wellenbelastungskoeffizient - resultiert aus dem Typ der dynamischen Belastung der Welle.
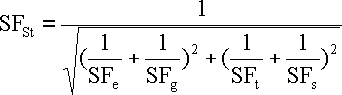
Statische Biegesicherheit
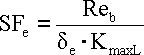
de - Biegespannung.
KmaxL - Maximaler Belastungskoeffizient - siehe. [6.20]
Reb - Biegefließgrenze
Ähnlich dann für partikuläre Sicherheit in Zug SFg, Torsion SFt und Scherung SFs
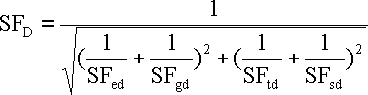
Dynamische Biegesicherheit
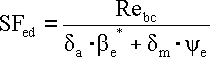
Mittlere Biegespannung
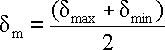
Biegespannungsamplitude
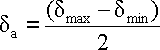
Rebc - Dauerbiegefestigkeit (bei einer wechselnden oder schwellenden Belastung ).
dmax - Höchstbiegespannung im
Belastungszyklus.
dmin - Mindestbiegespannung im
Belastungszyklus.
Gesamtbiegeformfaktor
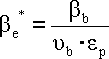
Kerbempfindlichkeitsfaktor in der Biegung
![]()
ye - Faktor für Werkstoffempfindlichkeit wegen der Asymmetrie im Zyklus.
ue - Teilgrößenfaktor.
ep - Oberflächenqualitätsfaktor.
ab - Kerbenfaktor.
q - Werkstoffempfindlichkeitsfaktor.
Ähnlich dann für partikuläre dynamische Sicherheit in der Zugbelastung SFgd, Torsion SFtd und Scherung SFsd
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung".
Die Berechnung selbst verläuft in VBA-Modul, deshalb ist sie für den Benutzer unerreichbar. Auf dem Blatt "Tabellen" können jedoch Werkstoffkoeffizienten, Kerbfaktoren betreffende Koeffizienten, Oberflächenfaktoren und Größenkoeffizienten korrigiert werden.