Das Programm ist für Toleranzanalyse linearer (1D) Maßketten bestimmt. Es löst folgende Aufgaben:
Bei allen Aufgaben ist es möglich mit normalisierten Toleranzwerten zu arbeiten, und zwar beim Vorschlag, wie auch bei der Optimierung der Maßkette.
Bei der Berechnung werden Daten, Verfahren, Algorithmen und Angaben aus der
Fachliteratur und ANSI, ISO, DIN und weiteren Normen verwendet.
Verzeichnis der Normen: ANSI B4.1, ISO 286, ISO 2768, DIN 7186
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Eine lineare Maßkette ist ein Komplex aus abhängigen parallelen Maßen, die so aneinander anschließen, dass sie ein geometrisch geschlossenes Rechteck bilden. Es können Abmaße sein, die die gegenseitige Lage von Elementen an einem Werkstück bestimmen (Abb. A), oder Abmaße mehrerer Werkstücke bei einer Montageeinheit (Abb. B).
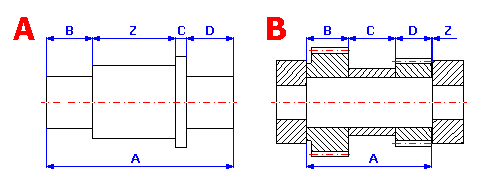
Die Maßkette setzt sich aus einzelnen Teilabmaßen
(Eingangsabmessungen) zusammen und wird mit dem Schließmaß
(resultierendes Maß) abgeschlossen. Teilabmaße (A,B,C,…) sind Abmaße, die
direkt auf der Zeichnung angegeben sind, oder sich aus den vorhergehenden
produktions- bzw. Montagevorgängen ergeben. Das Schließmaß (Z) stellt in der
gegebener Maßkette das resultierende Produktions- oder Montageabmaß dar,
welches sich durch das Zusammensetzen der Teilmaße als nicht angegebenes Abmaß
des Werkstückes, bzw. als Spiel, oder Übermaß bei der Montage ergibt. Die
Größe, Toleranz und Grenzabmaße des resultierenden Abmaßes sind direkt
abhängig von der Größe und Toleranz der Teilabmaße. Je nach dem, welche
Auswirkungen eine Änderung des Teilmaßes auf die Änderung des Schließmaßes
hat, wird zwischen zwei Arten von Teilmaßen unterschieden:
- vergrößernde Teilmaße - Teilmaße, durch deren Vergrößerung
das Schließmaß größer wird
- verkleinernde Teilmaße - Teilmaße, durch deren Vergrößerung
das Schließmaß kleiner wird
Bei der Lösung der Toleranzbeziehungen in den Maßketten kommen zwei Arten von Aufgaben vor:
Die Wahl der Berechnungsart der Toleranzen und Grenzabmaße der Teilmaße einer Maßkette hat Einfluss auf die Produktionsgenauigkeit und die Montageaustauschbarkeit von Teilen. Von ihr hängen die Produktions- und Betriebswirtschaftlichkeit ab. Bei der Lösung der Toleranzbeziehungen in den Maßketten werden in der technischen Praxis drei Grundmethoden verwendet:
Diese Methode wird am häufigsten verwendet, sie wird auch als Maximum - Minimum Methode bezeichnet. Sie geht von der Einhaltung der geforderten Grenzmaße des Schließmaßes für eine beliebige Kombination der tatsächlichen Größen der Teilmaße aus, also auch des oberen, wie unteren Grenzmaßes. Diese Methode garantiert eine vollständige Montage- und Betriebsaustauschbarkeit der Teile. Wird eine größere Genauigkeit des Schließmaßes gefordert, führt dies aber zu einer zu engen Toleranz der Teilmaße, also auch zu hohen Herstellkosten. Die WC Methode ist deshalb geeignet zur Lösung von Maßsystemen mit wenigen Teilmaßen, oder dann, wenn eine größere Toleranz des Schließmaßes zulässig ist. Am häufigsten wird sie in Einzel- oder Kleinserienproduktion verwendet.
Die WC Methode berechnet die Toleranz des resultierenden Abmaßes als eine Arithmetische Summe der Teilmaßtoleranzen. Die Größen des Schließmaßes sind also durch seinen Mittelwert bestimmt:
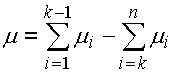
und durch die Gesamttoleranz:
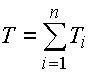
Grenzmaße des Schließmaßes sind dann durch diese Beziehungen gegeben:
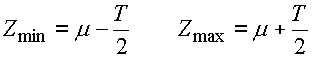
wo:
mi - Mittelwert des i-ten Teilmaßes
Ti - Toleranz des i-ten Teilmaßes
n - Gesamtanzahl der Teilmaße
i=1,..,k - Anzahl der vergrößernden Teilmaße
i=k,..,n - Anzahl der verkleinernden Teilmaße
Die statistischen Methoden der Berechnung der Maßketten sind an der Wahrscheinlichkeitsrechnung begründet. Diese Methoden gehen davon aus, dass bei einer zufälligen Auswahl von Werkstücken während der Montage die maximalen Werte der Grenzwerte bei mehreren Teilabmaßen nur selten zusammen auftreten, weil es sich um eine zusammengesetzte Wahrscheinlichkeit handelt. Genauso wenig wahrscheinlich ist das Auftreten der maximalen Grenzwerte bei der Produktion von einzelnen Teilabmaßen an einem Werkstück. Mit einem bestimmten, vorher festgelegten Risiko der Aussonderung einiger Werkstücke kann man also die Toleranzen der Teilabmaße im Kettenmaß vergrößern.
Die statistische Methode garantiert nur eine teilweise Austauschbarkeit bei der Montage mit einem niedrigem prozentuellem Anteil von ungünstigen Fällen (Ausschuss). Angesichts der größeren Toleranzen bei den Teilabmaßen führt sie aber zur Senkung der Produktionskosten. Sie wird vor allem in der Massen- und Großserienproduktion verwendet, wo die Einsparungen bei der Teilefertigung, verglichen mit den Kostenerhöhungen, die durch eine nicht vollständige Austauschbarkeit bei der Montage entstehen, überwiegen.
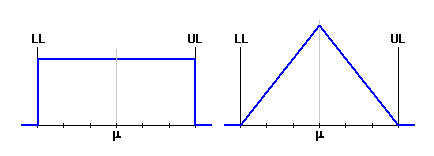
Die Dimensionen des Schließmaßes zeigen von der Mitte des Toleranzfeldes aus eine gewisse Streuung auf. Die Häufigkeit des Auftretens der einzelnen Werte richtet sich dabei nach den Gesetzen der mathematischen Statistik und entspricht in der absoluten Mehrheit der Fälle der Normalverteilung. Diese Verteilung wird durch die Gaußsche Kurve der Wahrscheinlichkeitsdichte beschrieben, in welcher die Häufigkeit des Auftretens des gegebenen Abmaßes "x" hierdurch gegeben ist:
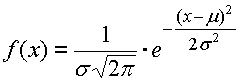
Die Form der Gaußscher Kurve wird durch zwei Parameter charakterisiert. Der Erwartungswert m bestimmt die Lage der maximalen Häufigkeit des Auftretens des resultierenden Abmaßes, die Standardabweichung s definiert die "Schlankheit" der Kurve.
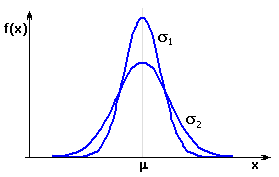
Die Fläche, die durch die Durchdringung der Gaußschen Kurve mit den geforderten Grenzwerten des Schließmaßes gebildet wird, stellt die voraussichtliche Ausbeute des Prozesses dar. Die Teile der Kurve, die außerhalb des Toleranzintervalls liegen, grenzen den Bereich ab, der den Ausschuss des Prozesses darstellt.
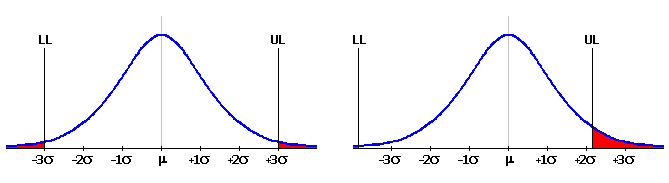
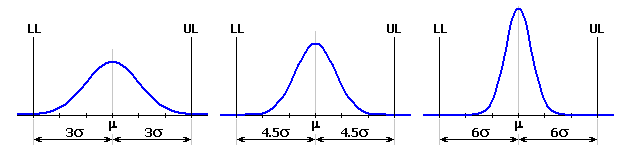
Im allgemeinen Maschinenbau wird meistens ein Produktionsprozess auf dem 3s Niveau als befriedigend geeignet angesehen. Das bedeutet, dass das obere Grenzmaß UL und das untere Grenzmaß LL des resultierenden Abmaßes von dem Erwartungswert m um 3s entfernt ist. Die Fläche der Gaußschen Kurve zwischen den beiden Grenzmaßen entspricht dann 99,73% der Gesamtfläche und stellt den Anteil der Erzeugnisse dar, die den spezifizierten Anforderungen entsprechen. Die Fläche außerhalb dieser Grenzmaße entspricht 0.27% und stellt ungeeignete Erzeugnisse dar.
| Grenzmaße | Prozessausbeute [%] | Anzahl der Ausschussteile per Million hergestellter Teile |
| m ± 1s | 68.2 | 317310 |
| m ± 2s | 95.4 | 45500 |
| m ± 3s | 99.73 | 2700 |
| m ± 3.5s | 99.95 | 465 |
| m ± 4s | 99.994 | 63 |
| m ± 4.5s | 99.9993 | 6.8 |
| m ± 5s | 99.99994 | 0.6 |
| m ± 6s | 99.9999998 | 0.002 |
Diese Methode der Berechnung ist traditionell und gleichzeitig die am weitesten verbreite Methode für die statistische Berechnung von Maßketten. Die RSS Methode geht von der Voraussetzung aus, dass die einzelnen Teilabmaße nach der Prozessqualität 3s hergestellt werden.
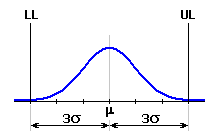
Ihre Grenzabmaße korrespondieren also mit dem Toleranzintervall m ± 3s, und die Standardabweichung ist gegeben durch:

Die Größen des Schließmaßes sind dann durch seinen Mittelwert bestimmt:
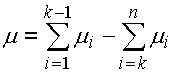
und durch die Standardabweichung:
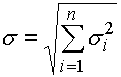
wo:
si - die Standardabweichung des
i-ten Teilmaßes ist
mi - Mittelwert des i-ten Teilmaßes
Ti - Toleranz des i-ten Teilmaßes
n - Gesamtanzahl der Teilmaße
i=1,..,k - Anzahl der vergrößernden Teilmaße
i=k,..,n - Anzahl der verkleinernden Teilmaße
Im allgemeinen Maschinenbau wird traditionell ein Produktionsprozess auf dem 3s Niveau als befriedigend geeignet angesehen. Das bedeutet voraussichtlich 2700 fehlerhafte Teile pro Million hergestellter Teile. Obwohl dieser Anteil an unbrauchbaren Teile auf den ersten Blick sehr gut erscheint, zeigt er sich in einigen Bereichen der Produktion oft als unzureichend. Zum weiteren ist es fast unmöglich, den mittleren Wert der Prozesscharakteristik langfristig genau in der Mitte des Toleranzfeldes zu halten. Durch den Einfluss verschiedener Faktoren (falsche Einstellung, Abnutzung der Werkzeuge und Vorrichtungen, Temperatureinflüsse usw.) kommt es bei großen Produktionsvolumina im laufe der Zeit zu einer Verschiebung des Erwartungswertes der Prozesscharakteristik. Üblich ist eine Verschiebung um 1.5s vom Idealwert. Das bedeutet bei traditionell gefassten Prozessen mit dem Qualitätslevel 3s eine Erhöhung des Anteiles von ungeeigneten Erzeugnissen auf ca. 67000 von einer Million erzeugter.
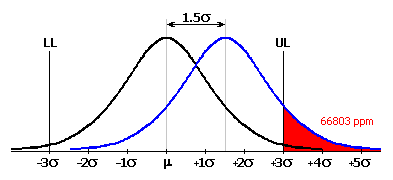
Es ist klar, dass ein Produktionsprozess mit diesem Anteil an Ausschuss unannehmbar ist. In letzter zeit wird also immer öfter für das Beurteilen der Qualität der Produktionsprozesse die moderne Methode "6 Sigma" erwendet. Das Konzept dieser Methode ist die Erreichung des Zieles, dass der Erwartungswert der Prozesscharakteristik um 6s von beiden Grenzabmaßen entfernt ist. Für so beschaffenen Produktionsprozess beträgt, auch bei vorausgesetzter Verschiebung des Erwartungswertes um 1.5s, der Anteil ungeeigneter Produkte nur 3.4 pro Million hergestellter Teile.
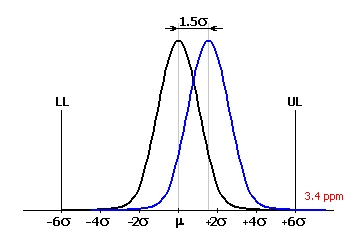
Die "6 Sigma" Methode ist relativ jung, sie erfuhr einer breiteren Anwendung erst in den 80er und 90er Jahren des vergangenen Jahrhunderts. In die Praxis wurde sie zum ersten mal von der Firma Motorola eingeführt und ist hauptsächlich in den USA verbreitet. Ihre Anwendung ist vorteilhaft bei der Forderung nach höherer Qualität der Produktionsprozesse und für große Produktionsvolumina, wo es zur einer Verschiebung des Erwartungswertes der Prozesscharakteristik kommen kann.
Die Methode "6 Sigma" ist eine Modifikation der Standard "RSS" Methode und sie führt in die Problematik der Lösung von Maßketten zwei neue Parameter ein (Cp, Cpk), die als Indexe der Prozessfähigkeit bezeichnet werden. Diese Fähigkeitsindexe dienen der Beurteilung der Prozessqualität.
Der Index Cp beschreibt die Qualität des Produktionsprozesses im Vergleich der spezifizierten Toleranzgrenzen mit der traditionellen Tauglichkeitsniveau 3s.
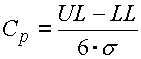
Für ein Prozess mit dem Toleranzintervall m ± 3s wird also Cp=1. Bei Prozessen mit hoher Qualität, wo die Toleranzgrenzen um ±6s von dem Erwartungswert entfernt sind, wird der Fähigkeitsindex Cp=2.
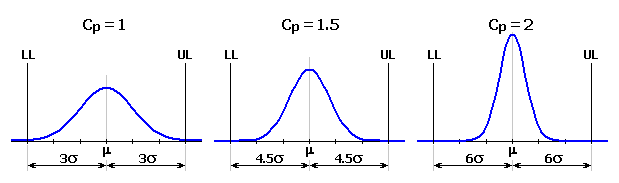
Der Index Cpk ist ein modifizierter Index Cp für den verschobenen Erwartungswert der Prozesscharakteristik.
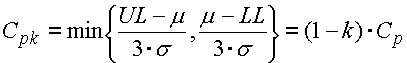
wo der Faktor für die Verschiebung k sich zwischen <0..1> bewegt und den relativen Wert der Verschiebung des Erwartungswertes bezogen auf die Hälfte des Toleranzintervalls angibt. Bei einer üblichen Verschiebung des Erwartungswertes der Prozesscharakteristik um 1.5s wird dann der Prozess mit der Qualität "6 Sigma" den Verschiebungsfaktor k=0,25 und den Fähigkeitsindex Cpk=1.5 haben.
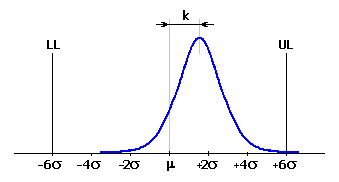
Die effektive Standardabweichung des Prozesses können wir dann so abschätzen:
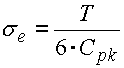
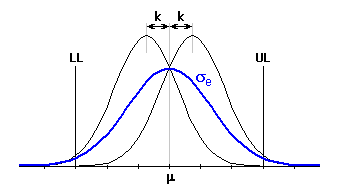
Bei der Verwendung der Fähigkeitsindexe auf alle Teilabmaße der Maßkette können wir dann, ähnlich wie bei der "RSS" Methode, die Dimensionen des Schließmaßes als sein Mittelwert m und die Standardabweichung beschreiben:
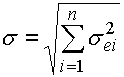
wo:
sei - die effektive Standardabweichung des i-ten Teilmaßes
ist
Als befriedigend bei der "6 Sigma" Methode wird ein Produktionsprozess mit der resultierenden Prozesstauglichkeit von 4.5s angesehen.
Die Methode der selektiven Montage wird bei Massen- und Großserienproduktion genauer Produkte verwendet, bei denen keine Betriebsaustauschbarkeit der Einzelteile innerhalb des Produktes gefordert wird. Der Montage des Produktes geht das Sortieren von Einzelteilen in Toleranzuntergruppen voraus. Die Produktionsabmaße der Einzelteile können mit größeren Toleranzen versehen werden. Eine engere Toleranz des resultierenden Abmaßes erreicht man dann durch sinnvolles Zusammenlegen (durch Kombinieren) der sortierten Untergruppen. Zur Bestimmung der Größe des Schließmaßes benutzt man die weiter oben beschriebene "WC" Methode mit dem Unterschied, dass in die Berechnung nicht die ganzen Produktionstoleranzen der Einzelteile eingehen, sondern nur die engeren Toleranzen, die für die gewählte Toleranzuntergruppe gelten.
Die selektive Montage ist eine sehr effektive Methode für die Auflösung von Maßketten, die eine maßgebliche Vergrößerung der Produktionstoleranzen der Einzelteile und damit eine deutliche Senkung der Produktionskosten erlaubt. Auf der anderen Seite stellt aber die Verwendung dieser Methode größere Anforderungen an die Montage des Produktes. Die Betriebskosten steigen auch, weil bei Abnutzung oder Beschädigung eines Einzelteiles gewöhnlich die ganze zusammengesetzte Baugruppe ausgetauscht werden muss.
Wenn die Methode der selektiven Montage effektiv sein soll, muss die Aufgabe der optimalen Auswahl (Kombination) der Einzelteile gelöst werden. Die Einzelteile müssen so zusammengelegt werden, dass mit einer gegebenen Anzahl angefertigter Einzelteile eine maximal mögliche Anzahl von Produkten zusammengestellt werde kann, die die Funktionsanforderungen erfüllen. Diese Aufgabe kann man in zwei Teile zerlegen:
1. Der konstruktive Teil der Aufgabe
Die Findung aller Kombinationen einzelner Untergruppen der Einzelteile für die das Schließmaß, die Funktionsanforderungen erfüllt.
Diese Aufgabe muss vor dem Produktionsstart gelöst werden, im Prozess des Maßkettenentwurfes. Die Anzahl geeigneter Kombinationen wird von der Gesamtproduktionstoleranz der Einzelteile, wie auch von der gewählten Anzahl der Toleranzsubintervalle abhängen. Die Maßkette sollte so gewählt werden, dass sich die Anzahl der annehmbaren Montagekombinationen in vernünftigen Grenzen bewegt.
Für eine kleine Zahl von geeigneten Kombinationen wird es wahrscheinlich nicht möglich sein alle produzierten Einzelteile für die Montage zu verwenden. So sinkt die Montageausbeute des Prozesses und die Produktion wird teuerer. Ein kritischer Hinweiß ist dann der Zustand, wenn beim Konstruktionsvorschlag sich eine der Untergruppen als nicht verwendbar zeigt.
Eine hohe Anzahl von geeigneten Kombinationen signalisiert zum Gegenteil einen uneffektiven Vorschlag. Die Toleranzkette könnte wahrscheinlich optimaler sein, mit größeren Toleranzen der Teilabmaße oder einer kleineren Anzahl der Toleranzsubintervalle.
2. Der technologische Teil der Aufgabe
Optimierung der Anzahl der zusammengesetzten Produkte für eine gegebene Anzahl von produzierten Einzelteilen in einzelnen Toleranzsubintervallen.
Diese Aufgabe muss im Produktionsverlauf wiederholt gelöst werden, und zwar immer beim Auffüllen von Lagerbeständen vor dem Beginn der eigentlichen Montage. Das Wesentliche dieser Aufgabe ist die Festlegung des optimalen Montageablaufes zur Erreichung der maximalmöglichen Anzahl von zusammengesetzten Produkten. Bei der Lösung dieser Aufgabe müssen wir also aus der Menge der annehmbaren Kombinationen den optimalen Satz der bei der Montage verwendeten Kombinationen auswählen und gleichzeitig die Anzahl der Produkte festlegen, die im Rahmen jeder verwendeten Kombination zusammengesetzt worden sind.
Der Optimierungsalgorithmus ist auf dem aufeinanderfolgenden Zusammensetzen einzelner Produkte durch das Entnehmen von Einzelteilen aus den ausgewählten Untergruppen begründet. Im ersten Schritt wird vom Rechenvorgang die minimal und maximal mögliche Anzahl der zusammengesetzten Produkte abgeschätzt. In den nächsten Schritten werden dann nach vorher ausgewählten Schema aus ausgewählten Untergruppen Einzelteile so entnommen, dass die untere Abschätzung der Anzahl der zusammengesetzten Produkte am schnellsten wächst und die obere Abschätzung am wenigsten abnimmt.
Die Lösung dieser Aufgabe ist in der Regel nicht eindeutig. Häufig findet man auch mehrere verschiedene Montageabläufe, die zu einer identischen Anzahl der zusammengesetzten Produkte führen. Deshalb wird als weiteres Optimierungskriterium die Anzahl der verwendeten Montagekombinationen verwendet. Die Minimierung der Anzahl der verwendeten Kombinationen führt zur Vereinfachung und Beschleunigung der Montage und damit zur Senkung der Produktionskosten. In manchen praktischen Applikationen sind oft beide Kriterien gleich wichtig.
Diese Zeile dient zum Umschalten des Einheitensystem des Rechenvorgangs und zur Wahl der genormten Toleranzen.
In der Auswahlliste das verlangte System von Berechnungsmaßeinheiten auswählen. Beim Umschalten der Einheiten werden alle Werte sofort umgerechnet.
Bei der Definition einer Maßkette in den Abschnitten [1.1, 3.2, 5.1, 7.1] ist für jede Dimension auch die dazugehörige Toleranz anzugeben. Als Arbeitserleichterung ist das Programm mit einem Tool für die automatische Wahl von genormten Toleranzen ausgestattet.
Das Programm beinhaltet ein Satz von Maßtoleranzen nach ISO bzw. ANSI. Im Hinblick auf den Typ der Abweichung und die verwendete Norm sind die Toleranzen in 5 Gruppen unterteilt:
Jede der Gruppen hat im Kopf des Mappe eine Reihe von Auswahllisten und Buttons. Stellen Sie in den Auswahllisten die erforderlichen Parameter der Toleranz bzw. Passung (Genauigkeitsgrad, Toleranzfeld,..) ein. Mit Hilfe der Buttons können Sie dann die Werte der gewählten Toleranz an die jeweilige Stelle in der Tabelle - in die Zeile mit der aktiven Zelle - einfügen.
Toleranzen nach ISO sind in der Norm in [mm] definiert und sind für die Berechnung in SI Einheiten bestimmt. Toleranzen nach ANSI sind in [in] definiert und für die Berechnung in "Imperial" Einheiten bestimmt. Bei Verwendung von genormten Toleranzen, die in anderen Einheiten definiert sind als im Programm eingestellt, werden die Maßabweichungen automatisch umgerechnet und gerundet.
Dieses Kapitel ermöglicht die Durchführung der Toleranzanalyse, Synthese und Optimierung von linearen Maßketten mit Hilfe der arithmetischen Methode "WC" bzw. der statistischen Methode "RSS".
Die Methode "Worst Case" wird verwendet, wenn eine vollständige Montage- und Betriebs-Austauschbarkeit gefordert ist und ist geeignet zur Lösung von Maßsystemen mit wenigen Teilmaßen, oder dann, wenn eine größere Toleranz des Schließmaßes zulässig ist. Die statistische Methode "Root Sum Squares" garantiert nur eine teilweise Montageaustauschbarkeit und wird zur Senkung der Produktionskosten bei einer Massen- und Großserienproduktion verwendet.
Die Aufgabe des Entwurfes und der Optimierung der Maßkette besteht aus folgenden Schritten:
Dieser Absatz ist für den Entwurf der Maßkette und die Optimierung der Toleranzen ausgewählter Teilabmaße bestimmt.
Diese Tabelle dient zur Definition der Größen einzelner Teilabmaße der Maßkette. Zu jedem Teilabmaß gehört eine Zeile der Tabelle. Die Bedeutung der Spalten der Tabelle wird aus folgender Beschreibung deutlich:
Spalte 1 - Benennung des Teilmaßes ist kein Pflichtparameter.
Spalte 2 - Geben Sie das Nominalmaß des Teilgliedes ein. Die
"vergrößernden" Teilmaße haben eine positiven Wert, die
"verkleinernden" geben Sie mit negativem Wert ein.
Spalte 3 - Geben Sie die obere und untere Toleranz des Abmaßes ein.
Durch Drücken des ausgewählten Buttons in der Kopfzeile der Mappe fügen Sie
in die Tabelle die für die gewählte Toleranz entsprechenden Abweichungen ein.
Spalte 4..7 - In diesen Spalten werden die Werte für die Grenzabmaße,
Mittelwert und die Standardabweichungen aller Teilabmaße ausgerechnet.
Spalte 8 - Markieren Sie mit Hilfe der Kästchen alle Teilmaße, deren
Toleranz optimiert werden soll. Das Markieren des Kästchens legt eine feste
(fixe) Toleranz fest, die bei der Optimierung unverändert bleibt.
Spalte 9,10 - Nach erfolgter Optimierung beinhalten diese Spalten die
vorgeschlagenen (optimierten) Toleranzen. In der linken Spalte sind die
Ergebnisse der Optimierung nach der arithmetischen "WC" Methode, in
der rechten dann für die statistische "RSS" Methode. Durch Drücken
des Buttons in der unteren Zeile der Tabelle übertragen Sie die vorgeschlagenen
Toleranzen in die Eingabespalte.
Dieser Absatz dient der Optimierung der Toleranzen gewählter Teilabmaße der in der Tabelle [1.1] definierten Maßkette. Geben Sie vor dem Start der Optimierung die geforderten Grenzmaße des Schließmaßes an [1.3] und stellen die Optimierungsparameter [1.6] ein. Starten Sie die Optimierung mit dem Button in Zeile [1.11].
Die Optimierung wird gleichzeitig für beide Berechnungsmethoden (WC, RSS) ausgeführt. Die vorgeschlagenen Toleranzen sind in der Tabelle [1.1] aufgeführt, die resultierenden Dimensionen des Schließmaßes finden Sie im Abschnitt [2].
Definieren Sie in diesem Abschnitt die geforderten Grenzdimensionen des Schließmaßes, die durch die Funktionsanforderungen an das Produkt gegeben sind.
Wählen Sie aus der Liste eine von den folgenden Betriebsarten für die Optimierung:
Beim Einhalten der Toleranzgröße korrigiert die Berechnung die Grenzabweichungen der ausgewählten Teilabmaße so, dass der Mittelwert des Schließmaßes am nächsten zur Mitte des durch die gegebenen Grenzen [1.3] geforderten Toleranzintervalls liegt. In Abhängigkeit von der Einstellung der Toleranzgenauigkeit [1.8] arbeitet das Programm in zwei Betriebarten:
Beim Einhalten des Mittelwertes des Toleranzintervalls korrigiert die Berechnung die Größe der Toleranzen der ausgewählten Teilabmaße so, dass die resultierenden Abmaße des Schließmaßes die durch die gegebenen Grenzen [1.3] geforderten Spezifikationen erfüllen.
Eine Kombination beider vorhergehenden Prozesse.
Wählen Sie in der Liste den Typ und die Genauigkeit der bei der Optimierung verwendeten Toleranzen.
Bei der Auswahl einer der ersten 5 Möglichkeiten aus der Liste wird die Größe der optimierten Toleranz mit vorher festgelegtem Grad der Genauigkeit (durch die Anzahl der Dezimalstellen) durch die Berechnung gegeben. Bei den optimierten Toleranzen wird dabei das gegenseitige Verhältnis ihrer Größen beibehalten.
Bei der Auswahl der restlichen zwei Möglichkeiten aus der Liste wird die Größe der optimierten Toleranzen den genormten Größen entsprechen. Bei der Berechnung in SI Einheiten werden dabei die genormten Toleranzen nach ISO 286 verwendet, für die Berechnung in den "Imperial" Einheiten nach der ANSI B4.1. Bei der Auswahl des Feldes "Gleichförmige Toleranzklasse" werden bei allen optimierten Dimensionen die genormten Toleranzen aus der gleichen Toleranzklasse verwendet.
Stellen Sie die minimale Größe (Genauigkeitsklasse) der Toleranzen ein, die bei der Optimierung verwendet werden darf.
Wählen Sie aus der Liste die minimale geforderte Ausbeute des Produktionsprozess.
In diesem Absatz werden in einer übersichtlichen Form die Detailparameter des Schließmaßes für die im Absatz [1] definierte Maßkette dargestellt. Zum Vergleich sind hier die resultierenden Dimensionen des Schließmaßes für die ursprünglichen, wie auch für die optimierten Toleranzen der Teilabmaße dargestellt.
Definieren Sie in diesem Abschnitt die geforderten Grenzdimensionen des Schließmaßes, die durch die Funktionsanforderungen an das Produkt gegeben sind.
In diesem Absatz sind die resultierenden Dimensionen des Schließmaßes bei der Verwendung der arithmetischen "Worst Case" Berechnungsmethode aufgeführt.
In diesem Absatz sind die Parameter des Schließmaßes bei der Verwendung der statistischen "Root Sum Squares" Berechnungsmethode aufgeführt.
Die Produktionsausbeute [2.13] gibt den angenommenen Anteil der Produkte an, die den spezifizierten Anforderungen entsprechen, d.h. der Produkte, bei denen sich die resultierende Dimension des Schließmaßes in dem durch die Randgrenzen gegebenem Intervall befindet [2.1]. Der Ausschuss des Produktionsprozesses [2.14] stellt den angenommenen Anteil von ungeeigneten Teilen pro Million hergestellter Teile dar.
In diesem Absatz werden die Grenzdimensionen des Schließmaßes für die gewählte Ausbeute des Produktionsprozesses berechnet.
Die in der Kapitel [A] verwendete Berechnung geht davon aus, dass das entworfene Teil nahe der Grundtemperatur von 20°C (68°F) verwendet wird, bei denen die Dimensionen und Toleranzen der Teilabmaße festgelegt wurden. Bei Teilen, die dauernd bei höheren Betriebstemperaturen verwendet werden, kommt es im Betrieb zu Veränderungen der Dimensionen. Dieses Kapitel ist für die Analyse von aufgrund einer Temperaturänderung deformierter linearer Maßketten bestimmt. Als Kontrolle der resultierenden Dimension des Schließmaßes kann die arithmetische "WC" Methode, oder die statistische "RSS" Methode verwendet werden.
Definieren Sie in diesem Abschnitt die Maßkette und die Betriebstemperatur, bei der das entworfene Teil verwendet wird.
Definieren Sie die angenommene Betriebstemperatur, bei der das entworfene Teil verwendet wird.
Diese Tabelle dient zur Definition der Größen einzelner Teilabmaße der Maßkette. Zu jedem Teilabmaß gehört eine Zeile der Tabelle. Die Bedeutung der Spalten der Tabelle wird aus folgender Beschreibung deutlich:
Spalte 1 - Benennung des Teilmaßes ist kein Pflichtparameter.
Spalte 2 - Geben Sie das Nominalmaß des Teilgliedes ein. Die
"vergrößernden" Teilmaße haben eine positiven Wert, die
"verkleinernden" geben Sie mit negativem Wert ein.
Spalte 3 - Geben Sie die obere und untere Toleranz des Abmaßes ein.
Durch Drücken des ausgewählten Buttons in der Kopfzeile der Mappe fügen Sie
in die Tabelle die für die gewählte Toleranz entsprechenden Abweichungen ein.
Spalte 4,5 - In diesen Spalten werden die Produktions- bzw.
Montagedimensionen der Teilabmaße ausgerechnet.
Spalte 6 - Wählen Sie aus der Liste das Material für das Teil.
Spalte 7 - Geben Sie den Koeffizient für die Wärmeausdehnung ein. Beim
Markieren des Kästchens in der Kopfzeile der Tabelle werden automatisch Werte
für das ausgewählte Material und die Betriebstemperatur vorgeschlagen [3.1].
Spalte 8,9 - In diesen Spalten werden die Dimensionen der Teilabmaße bei
der Betriebstemperatur ausgerechnet.
In diesem Absatz werden in einer übersichtlichen Form die Detailparameter des Schließmaßes für die im Abschnitt [3] definierte Maßkette dargestellt. Zum Vergleich sind hier die resultierenden Dimensionen des Schließmaßes bei der Montage (20°C) und bei der Betriebstemperatur dargestellt.
Geben Sie den Wärmeausdehnungskoeffizient für das Material des Schließmaßes.
Definieren Sie in diesem Absatz die geforderten Montagedimensionen des Schließgliedes. Die Grenzabmaße des Schließgliedes bei Betriebstemperatur werde automatisch in Abhängigkeit vom gewählten Temperaturausdehnungskoeffizient berechnet [4.1].
In diesem Absatz sind die resultierenden Dimensionen des Schließmaßes bei der Verwendung der arithmetischen "Worst Case" Berechnungsmethode aufgeführt.
In diesem Absatz sind die Parameter des Schließmaßes bei der Verwendung der statistischen "Root Sum Squares" Berechnungsmethode aufgeführt.
Die Produktionsausbeute [4.15] gibt den angenommenen Anteil der Produkte an, die den spezifizierten Anforderungen entsprechen, d.h. der Produkte, bei denen sich die resultierende Dimension des Schließmaßes in dem durch die Randgrenzen gegebenem Intervall befindet [4.3]. Der Ausschuss des Produktionsprozesses [4.16] stellt den angenommenen Anteil von ungeeigneten Teilen pro Million hergestellter Teile dar.
In diesem Absatz werden die Grenzdimensionen des Schließmaßes für die gewählte Ausbeute des Produktionsprozesses berechnet.
Dieses Kapitel ermöglicht die Durchführung der Toleranzanalyse von linearen Maßketten mit Hilfe der Methode "6 Sigma".
Die "6 Sigma" Methode ist eine moderne statistische Methode zur Beurteilung der Qualität der Produktionsprozesse. Ihre Anwendung ist vorteilhaft bei der Forderung nach höherer Qualität der Produktionsprozesse und für große Produktionsvolumina, wo es zur einer Verschiebung des Erwartungswertes der Prozesscharakteristik kommen kann. Das Konzept dieser Methode ist die Erreichung des Zieles, dass der Erwartungswert der Prozesscharakteristik um 6s von beiden Grenzabmaßen entfernt ist. Für so beschaffenen Produktionsprozess beträgt, auch bei vorausgesetzter Verschiebung des Erwartungswertes um 1.5s, der Anteil ungeeigneter Produkte nur 3.4 pro Million hergestellter Teile.

Dieser Abschnitt ist für den Entwurf der Maßkette bestimmt.
Diese Tabelle dient zur Definition der Größen einzelner Teilabmaße der Maßkette. Zu jedem Teilabmaß gehört eine Zeile der Tabelle. Die Bedeutung der Spalten der Tabelle wird aus folgender Beschreibung deutlich:
Spalte 1 - Benennung des Teilmaßes ist kein Pflichtparameter.
Spalte 2 - Geben Sie das Nominalmaß des Teilgliedes ein. Die
"vergrößernden" Teilabmaße haben eine positiven Wert, die
"verkleinernden" geben Sie als einen negativem Wert ein.
Spalte 3 - Geben Sie die obere und untere Toleranz des Abmaßes ein.
Durch Drücken des ausgewählten Buttons in der Kopfzeile der Mappe fügen Sie
in die Tabelle die für die gewählte Toleranz entsprechenden Abweichungen ein.
Spalte 4 - Wählen Sie aus der Liste den Typ der Verteilung der
Wahrscheinlichkeitsdichte. Standardmäßig wird zur Beschreibung der
Produktionsprozesse die Normalverteilung verwendet, die in der
absoluten Mehrheit der Fälle am Besten der tatsächlichen Verteilung der
zufälligen Prozessgrößen entspricht.
Spalte 5 - Geben Sie den Index der Prozessfähigkeit ein. Beim
Markieren des Kästchens in der Kopfzeile der Tabelle werden automatisch Werte
für den ausgewählten Typ der Wahrscheinlichkeitsverteilung verwendet.
Spalte 6 - Geben Sie den Verschiebungsfaktor des Erwartungswertes der
Prozesscharakteristik ein. Dieser Faktor gibt den Relativwert der Verschiebung
des Erwartungswertes bezogen auf die Hälfte des Toleranzintervalls an. Für ein
Produktionsprozess mit der "6 Sigma" Qualität wird im Allgemeinen mit
einem Verschiebungsfaktor k=0.25 gerechnet.
Spalte 7 - In dieser Spalte wird der modifizierte Eignungsindex für den
verschobenen Erwartungswert der Prozesscharakteristik berechnet.
Spalte 8,9 - In diesen Spalten werden die Erwartungswerte und die
effektive Standardabweichung des Prozesses berechnet.
In diesem Abschnitt werden in einer numerischen und graphischen Form die Detailparameter des ausgewählten Teilabmaßes dargestellt, so wie sie in der Tabelle [1.1] definiert wurden.
In diesem Abschnitt werden in einer übersichtlichen Form die Detailparameter des Schließmaßes für die im Abschnitt [5] definierte Maßkette dargestellt.
Definieren Sie in diesem Abschnitt die geforderten Grenzdimensionen des Schließmaßes, die durch die Funktionsanforderungen an das Produkt gegeben sind.
In diesem Abschnitt sind die Parameter des Schließmaßes bei der Verwendung der statistischen "6 Sigma" Berechnungsmethode aufgeführt.
Die Produktionsausbeute [6.11] gibt den angenommenen Anteil der Produkte an, die den spezifizierten Anforderungen entsprechen, d.h. der Produkte, bei denen sich die resultierende Dimension des Schließmaßes in dem durch die Randgrenzen gegebenem Intervall befindet [6.1]. Der Ausschuss des Produktionsprozesses [6.12] stellt den angenommenen Anteil von ungeeigneten Teilen pro Million hergestellter Teile dar.
In diesem Absatz werden die Grenzdimensionen des Schließmaßes für die gewählte Ausbeute des Produktionsprozesses berechnet.
Dieses Kapitel ermöglicht die Durchführung der Toleranzanalyse von linearen Maßketten mit Hilfe der Methode der Gruppenaustauschbarkeit (selektive Montage).
Die Methode der selektiven Montage wird bei Massen- und Großserienproduktion genauer Produkte verwendet, bei denen keine Betriebsaustauschbarkeit der Einzelteile innerhalb des Produktes gefordert wird. Der Montage des Produktes geht das Sortieren von Einzelteilen in Toleranzuntergruppen voraus. Die Produktionsabmaße der Einzelteile können mit größeren Toleranzen versehen werden. Eine engere Toleranz des resultierenden Abmaßes erreicht man dann durch sinnvolles Zusammenlegen (durch Kombinieren) der sortierten Untergruppen.
Die Aufgabe des Entwurfes der Maßkette besteht aus folgenden Schritten:
Außer des eigentlichen Vorschlages der Maßkette beinhaltet oft die Lösung auch eine Optimierung der Anzahl der zusammengesetzten Produkte für eine gegebene Anzahl von gefertigten Einzelteilen [9]. Diese Aufgabe muss im Produktionsverlauf wiederholt gelöst werden, und zwar immer beim Auffüllen von Lagerbeständen vor dem Beginn der eigentlichen Montage.
Dieser Abschnitt ist für den Entwurf und Kontrolle der Maßkette bestimmt.
Definieren Sie in der Tabelle [7.1] die Anzahl, Abmessungen und Toleranzen aller Teile aus denen das Endprodukt zusammengesetzt wird. Weiter wählen Sie für jedes Teil die Anzahl von Toleranzuntergruppen (der Subintervalle), in die vor der Montage das Teil einsortiert wird. Im Abschnitt [7.2] stellen Sie dann die Grenzabmaße für das Schließmaß für eine beliebige Montagekombination der sortierten Untergruppen der Einzelteile fest.
Diese Tabelle dient zur Definition der Größen einzelner Teilglieder (der Einzelteile) der Maßkette. Zu jedem Einzelteil gehört eine Zeile der Tabelle. Die Bedeutung der Spalten der Tabelle wird aus folgender Beschreibung deutlich:
Spalte 1 - Geben Sie die Anzahl von identischen Einzelteilen die in
die Maßkette eingehen.
Spalte 2 - Benennung des Einzelteiles ist kein Pflichtparameter.
Spalte 3 - Geben Sie das Nominalmaß des Teilgliedes ein. Die
"vergrößernden" Teilabmaße haben eine positiven Wert, die
"verkleinernden" geben Sie als einen negativem Wert ein.
Spalte 4 - Geben Sie die obere und untere Toleranz des Abmaßes ein.
Durch Drücken des ausgewählten Buttons in der Kopfzeile der Mappe fügen Sie
in die Tabelle die für die gewählte Toleranz entsprechenden Abweichungen ein.
Spalte 5 - Stellen Sie die Anzahl von Toleranzuntergruppen (der
Subintervalle) ein, in die vor der Montage das Teil einsortiert wird. Mit der
Auswahl in der Kopfzeile der Tabelle können Sie die gleiche Anzahl von
Untergruppen für alle Einzelteile einstellen.
Spalte 6..11 - In diesen Spalten werden die Grenzabmaße aller
Toleranzsubintervalle ausgerechnet. Die einzelnen Untergruppen sind im Kopf mit
einem Nummerindex gekennzeichnet. Zusammen mit der Kennzeichnung des
Einzelteiles dient dann dieser Index zu einer eindeutigen Beschreibung der
Montageuntergruppe (A1, A2, B1, B2, B3, ...).
In der ersten Zeile der Tabelle sind die Grenzabmaße des Schließmaßes dargestellt, die mit Hilfe der "Worst Case" Methode für die vollen Toleranzen der Einzelteile bestimmt worden sind. Diese Angabe dient lediglich der Orientierung und hat vor Allem eine Bedeutung für die Zentrierung des Vorschlages. Für einen gut und effektiv durchgeführten Lösungsvorschlag der Maßkette sollte sich der hier angegebener Erwartungswert so weit wie möglich der geforderten Dimension annähern [8.7].
In der zweiten Zeile stellen Sie dann die Grenzabmaße für das Schließmaß für eine beliebige Montagekombination der sortierten Untergruppen der Einzelteile fest. Die geforderte Montagekombination können Sie durch die Wahl entsprechender Toleranzuntergruppen in den Auswahllisten einstellen.
Ein unteilbarer Bestandteil des Lösungsvorschlages einer Maßkette ist die Lösung der Aufgabe der richtigen Paarung von Einzelteilen. In dieser Aufgabe geht es um die Findung solcher Montagekombinationen einzelner Untergruppen der Einzelteile für die das Schließmaß die Funktionsanforderungen erfüllt. Die Gesamtanzahl gefundener Kombinationen ist dann ein Maßstab für die Beurteilung der Qualität des Vorschlages. Die Maßkette sollte so gewählt werden, dass sich die Anzahl der annehmbaren Montagekombinationen in vernünftigen Grenzen bewegt.
Für eine kleine Zahl von geeigneten Kombinationen wird es wahrscheinlich nicht möglich sein alle produzierten Einzelteile für die Montage zu verwenden. So sinkt die Montageausbeute des Prozesses und die Produktion wird teuerer. Ein kritischer Hinweiß ist dann der Zustand, wenn beim Konstruktionsvorschlag sich eine der Untergruppen als nicht verwendbar zeigt.
Eine hohe Anzahl von geeigneten Kombinationen signalisiert zum Gegenteil einen uneffektiven Vorschlag. Die Toleranzkette könnte wahrscheinlich optimaler sein, mit größeren Toleranzen der Teilabmaße oder einer kleineren Anzahl der Toleranzsubintervalle.
Die Methode der selektiven Montage garantiert nur eine teilweise (Gruppen) Montageaustauschbarkeit im Rahmen der ausgewählten Montagekombinationen. Bei Abnutzung oder Beschädigung eines Einzelteiles im Betrieb ist es also notwendig die ganze zusammengesetzte Baugruppe auszutauschen. Die Methode der selektiven Montage wird deshalb vor allem bei der Produktion genauer Produkte verwendet, bei denen keine Betriebsaustauschbarkeit der Einzelteile innerhalb des Produktes gefordert wird.
Auch wenn das eine Erhöhung der Produktionskosten mit sich bringt, kann es bei manchen Produkten trotzdem ökonomisch von Vorteil sein, zumindest bei einem Einzelteil seine völlige Betriebsaustauschbarkeit sicherzustellen. Für eine so formulierte Forderung begegnen wir bei der Lösung der Aufgabe der selektiven Montage zwei verschiedenen Fällen (Vorgehen) der Lösung:
Definieren Sie in diesem Abschnitt die geforderten Grenzdimensionen des Schließmaßes, die durch die Funktionsanforderungen an das Produkt gegeben sind. In der ersten Spalte sind die Grenzmaße des Schließmaßes bei der Montage des Produktes angegeben. In der zweiten Spalte dann die Grenzabmaße beim Austausch des ausgewählten Einzelteiles.
Dieser Abschnitt dient der Suche aller Montagekombinationen, für die das Schließmaß die in den Abschnitten [8.1, 8.4] definierten Funktionsforderungen erfüllt. Das Programm arbeitet in zwei Betriebsarten:
Die Betriebsart der Suche können Sie in der Auswahl [8.9] einstellen. Die Suche wird mit dem Button in Zeile [8.10] gestartet, die Ergebnisse sind im Abschnitt [8.11] aufgeführt.
Dieser Parameter gibt die Gesamtanzahl aller Montagekombinationen an, mit deren Hilfe das Produkt zusammengesetzt werden kann.
Dieser Parameter gibt die Anzahl aller gefundenen Montagekombinationen an, für die das Schließmaß die in den Abschnitten [8.1, 8.4] definierten Funktionsforderungen erfüllt. Die Gesamtanzahl gefundener Kombinationen ist dann ein Maßstab für die Beurteilung der Qualität des Vorschlages. Die Maßkette sollte so gewählt werden, dass sich die Anzahl der annehmbaren Montagekombinationen in vernünftigen Grenzen bewegt.
Für eine kleine Zahl von geeigneten Kombinationen wird es wahrscheinlich nicht möglich sein alle produzierten Einzelteile für die Montage zu verwenden. So sinkt die Montageausbeute des Prozesses und die Produktion wird teuerer.
Eine hohe Anzahl von geeigneten Kombinationen signalisiert zum Gegenteil einen uneffektiven Vorschlag. Die Toleranzkette könnte wahrscheinlich optimaler sein, mit größeren Toleranzen der Teilabmaße oder einer kleineren Anzahl der Toleranzsubintervalle.
In der Tabelle der geeigneten Kombinationen sind die Montagekombinationen aufgeführt, für die das Schließmaß die in den Abschnitten [8.1, 8.4] definierten Funktionsforderungen erfüllt. Die resultierenden Dimensionen des Schließmaßes sind für die gewählte Kombination im Abschnitt [8.15] aufgeführt.
In der Tabelle der nichtgenutzten Untergruppen sind alle Toleranzuntergruppen (Subintervalle) aufgeführt, für die es nicht möglich ist eine annehmbare Montagekombination zu finden. Produkte, die in diesen Untergruppen einsortiert sind, können dann bei der Montage nicht verwendet werden. So sinkt die Montageausbeute des Prozesses und die Produktion wird teuerer. Bei richtig vorgeschlagener Maßkette sollte diese Tabelle leer bleiben.
In diesem Abschnitt werden in einer numerischen und graphischen Form die resultierenden Dimensionen des Schließmaßes für die in der Tabelle [8.14] ausgewählten Montagekombinationen dargestellt. In der ersten Spalte sind die Grenzmaße des Schließmaßes bei der Montage des Produktes angegeben. In der zweiten Spalte dann die Grenzabmaße beim Austausch des ausgewählten Einzelteiles.
Wenn die Methode der selektiven Montage effektiv sein soll, muss die Aufgabe der optimalen Auswahl (Kombination) der Einzelteile gelöst werden. Die Einzelteile müssen so zusammengelegt werden, dass mit einer gegebenen Anzahl angefertigter Einzelteile eine maximal mögliche Anzahl von Produkten zusammengestellt werde kann, die die Funktionsanforderungen erfüllen.
Diese Aufgabe muss im Produktionsverlauf wiederholt gelöst werden, und zwar immer beim Auffüllen von Lagerbeständen vor dem Beginn der eigentlichen Montage. Das Wesentliche dieser Aufgabe ist die Festlegung des optimalen Montageablaufes zur Erreichung der maximalmöglichen Anzahl von zusammengesetzten Produkten. Bei der Lösung dieser Aufgabe müssen wir also aus der Menge der annehmbaren Kombinationen [8.14] den optimalen Satz der bei der Montage verwendeten Kombinationen auswählen und gleichzeitig die Anzahl der Produkte festlegen, die im Rahmen jeder verwendeten Kombination zusammengesetzt worden sind.
Die Lösung dieser Aufgabe ist in der Regel nicht eindeutig. Häufig findet man auch mehrere verschiedene Montageabläufe, die zu einer identischen Anzahl der zusammengesetzten Produkte führen. Deshalb wird als weiteres Optimierungskriterium die Anzahl der verwendeten Montagekombinationen verwendet. Die Minimierung der Anzahl der verwendeten Kombinationen führt zur Vereinfachung und Beschleunigung der Montage und damit zur Senkung der Produktionskosten. In manchen praktischen Applikationen sind oft beide Kriterien gleich wichtig.
Geben Sie in der Tabelle die Anzahl der gefertigten Einzelteile in einzelnen Toleranzsubintervallen.
Wählen Sie die gewünschte Optimierungsmethode aus der Auswahlliste.
Außer der Forderung nach der Zusammenstellung einer maximalen Anzahl von Produkten kommt in der Praxis oft die Forderung nach der Minimierung der Anzahl von Montagekombinationen vor, die beim Zusammensetzen des Produktes verwendet werden. Bei sinkender Anzahl der verwendeten Kombinationen sinkt aber auch die Gesamtanzahl der zusammengesetzter Produkte. Es wird deutlich, dass diese beiden Forderungen sich gegenseitig entgegenwirken. Deshalb muss beider Optimierung ein Parameter definiert werden, der das Gewicht (die Wichtigkeit) der einzelnen Kriterien ausdrückt. Das gegenseitige Verhältnis der Wichtigkeit beider Kriterien stellen Sie mit Hilfe des Schiebers ein.
Das Ergebnis der Aufgabe der Optimierung der Anzahl von zusammengesetzten Produkten ist in der Regel nicht eindeutig. Häufig findet man auch mehrere verschiedene Montageabläufe, die zu einer identischen Anzahl der zusammengesetzten Produkte führen. Die Berechnung bietet deshalb die Möglichkeit der Auswahl aus mehreren unterschiedlichen Lösungsansätzen bei der Verwendung von verschiedenen Optimierungsalgorithmen. Die Wahl des Lösungsweges stellen Sie in der Auswahlliste vor dem Start der Optimierung.
In diesem Abschnitt finden Sie die Basisparameter für die Qualität des vorgeschlagenen Montageverlaufes. Detailbeschreibung des optimierten Montageverlaufes finden Sie in der Tabelle [9.12].
In dieser Tabelle finden Sie die Detailbeschreibung des optimierten Montageverlaufes. In der linken Spalte sind alle Montagekombinationen aufgeführt, die für das Zusammensetzten des Produktes verwendet wurden. In der rechten Spalte ist dann die Anzahl der im Rahmen jeder Kombination zusammengesetzten Produkte angegeben.
In dieser Tabelle ist die Anzahl der übriggebliebenen (nichtgenutzten) Einzelteile, die bei der Montage des Produktes nicht genutzt werden konnten.
Zur Illustration der Problematik der Toleranzanalyse linearer Maßketten wurde die Hilfe durch ein paar praktische Beispiele für die Verwendung des Programms ergänzt:
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.