Program je určen pro řešení nejčastějších úloh z oblasti termomechaniky, se kterými se konstruktér při řešení obvyklých problémů potká.
Program řeší úlohy z oblasti:
1. Energie: ohřátí a ochlazení, změna skupenství,
výhřevnost paliv
2. Ideální plyn: stav a změna stavu, termodynamická
soustava
3. Přestup tepla složenou stěnou (vedení, sálání,
konvekce)
4. Řešení žebrovaných stěn a svazků trubek
5. Podélná změna teploty v potrubí, změna teploty a
doba ochlazování v zásobníku
6. Výměníky tepla
7. Přenos tepla zářením
8. Výkon slunečního záření (doba, čas, poloha,
prostředí, orientace plochy …)
9. Příprava dat pro použití doplňku "Řešitel"
Výpočty obsahují stovky předdefinovaných materiálů, kapalin a plynů, periodickou
tabulku prvků, přepočty jednotek a další. K dispozici
je také množství řešených příkladů.
Ve výpočtu jsou použita data, postupy, algoritmy a údaje z odborné literatury,
norem a firemních katalogů.
[01] YUNUS A. ÇENGEL, AFSHIN J. GHAJAR: Heat and Mass Transfer: Fundamentals
& Applications, 5th Edition, McGraw-Hill Education.
[02] YUNUS A. ÇENGEL: Heat Transfer a Practical Approach, Second Edition.
[03] MORAN, M.J., SHAPIO, H.N.: Fundamentals of engineering thermodynamics. 8th
Edition New York: John Wiley a sons, 1990.
[04] DEWITT, BERGMAN, LAVINE: Fundamentals of Heat and Mass Transfer 6th Edition
[05] WARREN M.ROHSENOW, JAMES R.HARTNETT, YOUNG I.CHO: Handbook of Heat
Transfer, 3th Edition, McGraw-Hill
[06] SCHLUNDER, BELL, HEWITT, SPALDING: Heat Exchanger
Design Handbook, VDI-Verlag GmbH, 1983.
[07] LOIS THEODORE: Heat Transfer Applications for the
Practicing Engineer, John Wiley & Sons, Inc., 2011.
[08] MYER KUTZ: Heat-Transfer Calculations,
McGraw-Hill
[09] HOLMAN, J.P.: Heat Transfer, 10th. Edition, New
York: McGraw-Hill
[10] HOLMAN, J.P. Thermodynamics. 4th. New York:
McGraw-Hill Book Company, 1988. 780 s. ISBN 0-07-029633-2.
[11] MOHAMED M. EL-AWAD: Optimisation Analyses of
Fluid- Thermal Systems Using Excel,
[12] FRANK KREITH, RAJ MANGLIK, MARK BOHN: Principles
of Heat Transfer, Cengage Learning, Inc., 2011
[13] HORÁK VLADIMÍR, STŘEDA IVO: Mechanika tekutin
- Termomechanika, Strojírenská příručka, Scientia sro.
[14] RANEVI,K. Termodynamické tabulky. 1.vyd.
Bratislava: ALFA 1984. 313s. [L5] HAEK, P. Tabulky pro tepelnou techniku. 1
.vyd. VB Ostrava, 1980, 247 s.
[15] SAZIMA,M., KMON1OEK,V., SCHNELER,J. Teplo. 1.vyd.
Praha: SNTL, 1989. 588 s. Technický průvodce. ISBN 80-03-00043-2.
[16] M.A.MICHEJEV: Základy sdílení tepla, Průmyslové
vydavatelství, 1952
[17] PETRAK,J., DVOAK, Z., KLAZAR, L., SYNEK, V.
Chiadivo R134a, (1.vyd.) VUT, 1993. 72s.
[18] MIROSLAV JÍLEK, ZDENĚK RANDA: Termomechanika -
sbírka příkladů, ČVUT, 2004
Informace o syntaxi a ovládání výpočtu naleznete v dokumentu "Ovládání, struktura a syntaxe výpočtů".
Informace o účelu, použití a ovládání odstavce "Informace o projektu" naleznete v dokumentu "Informace o projektu".
E = m * ΔT * Cp
E ... Energie [J]
m ... Hmotnost [kg]
ΔT ... Změna teploty [K]
Cp ... Měrná tepelná kapacita [J/kg/K]
EM = m * CpM * 1000
EB = m * CpB * 1000
EM, EB ... Energie [J]
CpM ... Měrná tepelná kapacita tání [kJ/kg]
CpB ... Měrná tepelná kapacita varu [kJ/kg]
E = m * HHV * (η / 100) * 1000000
E ... Energie [J]
m ... Hmotnost spáleného paliva [kg]
HHV ... Spalné teplo [MJ/kg]
η ... Účinnost spalování [%]
Stav (termodynamické) soustavy je charakterizován stavovými veličinami. Vztah mezi stavovými veličinami je dán stavovými rovnicemi.
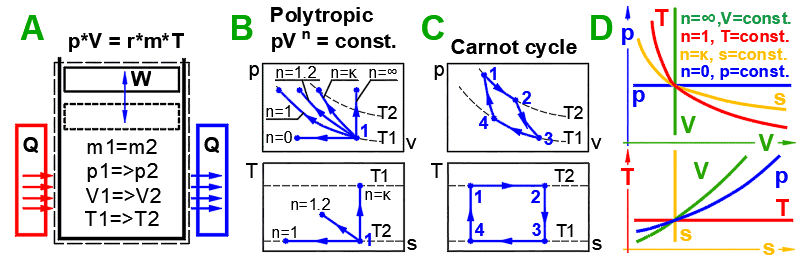
A … Příklad jednoduché termodynamické soustavy, ideální plyn
p*V=m*r*T.
B … Vratné děje je možné popsat obecněji jako polytropické děje, kdy je tepelná
kapacita (uzavřené) soustavy konstantní. Při polytropickém ději se obecně mění
všechny stavové veličiny (p,V,T). Pro polytropický děj v ideálním plynu platí
rovnice p*V^n = const. V diagramu p-V, T-s jsou vyznačené křivky změn pro různá
n.
C ... Carnotův cyklus. Příklad ideálního tepelného stroje, který se skládá ze
dvou izotermických a dvou adiabatických dějů.
D ... Křivky základních vratných stavových změn:
p * V = m * r * T
r = R / M
M = m / N
p ... Absolutní tlak [Pa]
V ... Objem [m^3]
m ... Hmotnost [kg]
T ... Teplota [°K]
R ... Univerzální plynová konstanta R=8314.46261815324 [J/kmol/K]
M ... Molární hmotnost plynu [kg/kmol] (vzduch 28.966 kg/kmol)
N ... Látkové množství [kmol]
r ... Měrná plynová konstanta [J/kg/K] (vzduch 287.0427 J/kg/K)
u = u0 + cv * (T - T0) [J/kg]
Δu = cv * (T2 - T1) [J/kg]
h = h0 + cp * (T - T0) [J/kg]
Δh = cp * (T2 - T1) [J/kg]
ds = s2 - s1 = cp * Ln(T2/T1) - r * Ln(p2 / p1)
ds = s2 - s1 = cv * Ln(T2/T1) + r * Ln(v2 / v1)
cp - cv = r
cp ... Měrná tepelná kapacita - konstantní tlak [J/kg/K]
cv ... Měrná tepelná kapacita - konstantní objem [J/kg/K]
κ = cp / cv
cv = r / (κ - 1)
cp = κ * cv
p1 * V1 = p2 * V2
V1 / V2 = T1 / T2
Vratné děje je možné považovat za obecnější polytropické děje pro které platí:
p * V^n = konstanta
T2 / T1 = (V1 / V2)^(n-1) = (p2 / p1)^((n-1)/n)
n ... Polytropicky exponent [~]
Pro vybrané hodnoty n pak platí:
n=0 ,p=const, Isobaric, (dp=0, wt=0, q=Δh, w=Δh-Δu)
n=1 ,T=const, Isotermic, (dT=0, Δu=Δh=0, q=w=wt)
n=κ ,s=const, Isoentropic, (ds=0, q=0, w=-Δu, wt=-Δh)
n=∞ ,v=const, Isochoric, (dv=0, w=0, q=Δu, wt=Δu-Δh)
n = ln(p2 / p1) / (ln(p2 / p1) - ln(T2 / T1))
n = (ln(V2 / V1) - ln(T2 / T1)) / ln(V2 / V1)
q = cn * (T2 - T1) [J/kg]
cn =
cv * (n - κ) / (n - 1)
cn ... Polytropická
měrná tepelná kapacita
[J/kg/K]
w = q - Δu [J/kg]
wt = q - Δh = n * w [J/kg]
Výpočet parametrů plynu který vnikne smíšením dvou částí s různými parametry p,V,T.
m = m1 + m2
p = m / M * R * T / V
V = V1 + V2
T = (m1 * T1 + m2 * T2) / (m1 + m2)
Jedná se o často řešený úkol. A to jak pro strojní inženýrství, tak pro jiné navazující obory.
Tuto problematiku je samozřejmě možné řešit pomocí odpovídajících simulačních programů. Přesto však pro základní odhad a velkou část těchto úloh většinou stačí jednoduchý výpočet postavený na základních fyzikálních vztazích.
Rozdělení je na přestup tepla vedením, prouděním a zářením. Níže jsou uvedené příslušné vztahy.
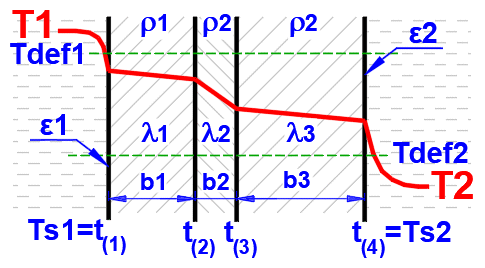
Ve výpočtech jsou použité následující vztahy pro složenou rovinnou, válcovou a kulovou stěnu (max 10 vrstev).
r(i) = D(i)/2
q' = -λ * ΔT
qp' = (t(1) - t(n+1)) / Rp
qp' = (t(1) - t(n+1))
/ Σ (b(i) /
λ(i)) ..... [i=1...n]
Tepelný odpor [(m²K)/W]
R = Rp =
Σ (b(i) /
λ(i)) ..... [i=1...n]
qc' = (t(1) - t(n+1)) / Rc
qc' = (t(1) - t(n+1))
/ (1/(2 * 3.14) * Σ
((1/λ(i))
* ln(r(i+1)/r(i))))
..... [i=1...n]
Lineární tepelný odpor [(mK)/W]
Rc = (1
/
(2 * 3.14159) *
Σ
((1/λ(i))
* ln(r(i+1)/r(i))))
..... [i=1...n]
Tepelný odpor na jednotku vnitřní plochy
[(m²K)/W]
R =
Rc * (2 * 3.14159 * r(1))
qs' = (t(1) - t(n+1)) / Rs
qs' = (t(1) - t(n+1))
/ (1/(4 * 3.14) * Σ
((1/λ(i))
* (1/r(i) - 1/r(i+1)))
..... [i=1...n]
Tepelný odpor kulové plochy [K/W]
Rs = (1
/
(4 * 3.14159) *
Σ
((1/λ(i))
* (1/r(i) - 1/r(i+1)))
..... [i=1...n]
Tepelný odpor na jednotku vnitřní plochy
[(m²K)/W]
R =
Rs * (4 * 3.14159 * r(1)²)
K přenosu tepla dochází v okolí stěny v mezní vrstvě, která vzniká z rozdílu teplot. Samotný přenos tepla pak závisí na celé řadě parametrů (parametry tekutiny, druh proudění, tvar plochy...).
Jak pro nucené
(médium je hnané) tak pro
volné proudění je možné použít celé řady vzorců, které jsou založené na
měření a aproximaci hodnot (viz. literatura). Ty
nejdůležitější a často používané, jsou použité v tomto výpočtu. Vzorce, rozsah
platných hodnot a odpovídající grafy jsou uvedené níže. Pro grafy jsou zvolené
takové rozměrové hodnoty, které mohou odpovídat běžnému použití. V grafech je
pro porovnání volen vzduch a voda, jako nejčastější pracovní médium.
Pro grafy jsou zvolené jednotky: Teplota [°C], rozměry
[mm]
Většina používaných vztahů jsou empirické rovnice, přičemž výsledky jsou vyjadřovány pomocí závislostí bezrozměrných kritérií podobnosti.
Grashoferovo číslo Gr = 9.81 * L * β *
abs(T - Ts) / ν
Nusseltovo číslo Nu = hc * L / λ
Prandtlovo číslo Pr = (µ / Rho) / (λ / (Cp * Rho))
Rayleighovo číslo Ra = Gr * Pr
Reynoldsovo číslo Re = (L * V) / ν
Obecně je používán vzorec:
hc = (Nu *
λ) / L
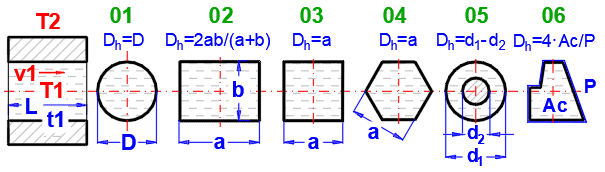
01a. Proudění v potrubí - kružnice
(D,L): [Tdef = (T+Ts)/2, 0.1<Re<1e7] ...
(Strojírenská příručka, Graetz)
hc = (Nu *
λ) / D
Nu = (3.65 + (0.0668 * Re * Pr * (D/L)) / (1 + 0.045 * (Re * Pr *
(D/L))^(2/3))) * (μ / μs)^0.14 ..... [Re<2300]
Nu = 21 * (Pr * (D/L))^0.33 * (Re/2300)^(LOG(L/D)) ..... [Re*Pr*(D/L)>12, Pr>0.5,
L/D>30, 2300<Re<5000]
Nu = 3.66 * (Re/2300)^(2.3 + LOG(Pr) ..... [Re*Pr*(D/L)<12, Pr>0.5, L/D>30,
2300<Re<5000]
Nu = E * (0.023 * Pr^H * Re^0.8) * K ..... [0.5<Ts/Tdef<1 (°K),
1e4<Re<2e6]
Nu = E * (0.023 * Pr^H * Re^0.8) * K ..... [1<Ts/Tdef<3.5 (°K),
1e4<Re<2e6]
Koeficient H
H = 0.4 ..... T<Ts
H = 0.3 ..... T>Ts
Koeficient K
K = 1.27 - 0.27 * (Ts/Tdef) ..... [0.5<Ts/Tdef<1, Ts(°K),
T(°K)]
K = (Ts/Tdef)^(-0.55) ..... [1<Ts/Tdef<3.5, Ts(°K),
T(°K)]
Koeficient E
| ▼ Re... L/D ► | 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 1000 |
| 1.00E+04 | 1.65 | 1.50 | 1.34 | 1.23 | 1.17 | 1.13 | 1.07 | 1.03 | 1.00 | 1.00 |
| 2.00E+04 | 1.51 | 1.40 | 1.27 | 1.18 | 1.13 | 1.10 | 1.05 | 1.02 | 1.00 | 1.00 |
| 5.00E+04 | 1.34 | 1.27 | 1.18 | 1.13 | 1.10 | 1.08 | 1.04 | 1.02 | 1.00 | 1.00 |
| 1.00E+05 | 1.28 | 1.22 | 1.15 | 1.10 | 1.08 | 1.05 | 1.03 | 1.02 | 1.00 | 1.00 |
| 1.00E+06 | 1.14 | 1.11 | 1.08 | 1.05 | 1.04 | 1.03 | 1.02 | 1.01 | 1.00 | 1.00 |
| 1.00E+12 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
01b. Proudění v potrubí - kružnice
(D,L): [Tdef = (T+Ts)/2, 0.1<Re<1e7] ... (Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D
Nu = (3.65 + (0.0668 * Re * Pr * (D/L)) / (1 + 0.045 * (Re * Pr *
(D/L))^(2/3))) * (μ / μs)^0.14 ..... [Re<2100]
Nu = 0.023
* Re^0.8
*
Pr^H ..... [0.5<Pr<160,
6000<Re<1e7, L/D<60]
Koeficient H
H = 0.4 .... T<Ts
H = 0.3 .... T>Ts
01c.
Proudění v potrubí - kružnice
(D,L): [Tdef = (T+Ts)/2, 0.1<Re<1e7] ...
(Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ) / D
Nu = 1.86 * (Re * Pr * (D / L))^(1/3) * (μ / μs)^0.14
..... [Re<2100]
Nu =0.027 * Re^0.8 * Pr^(1/3) *
(μ / μs)^0.14 ..... [0.5
< Pr < 10000,
Re>2100]
Re-Nu graf pro vzduch a vodu (T ... [°C], D,Dh,L ... [mm])
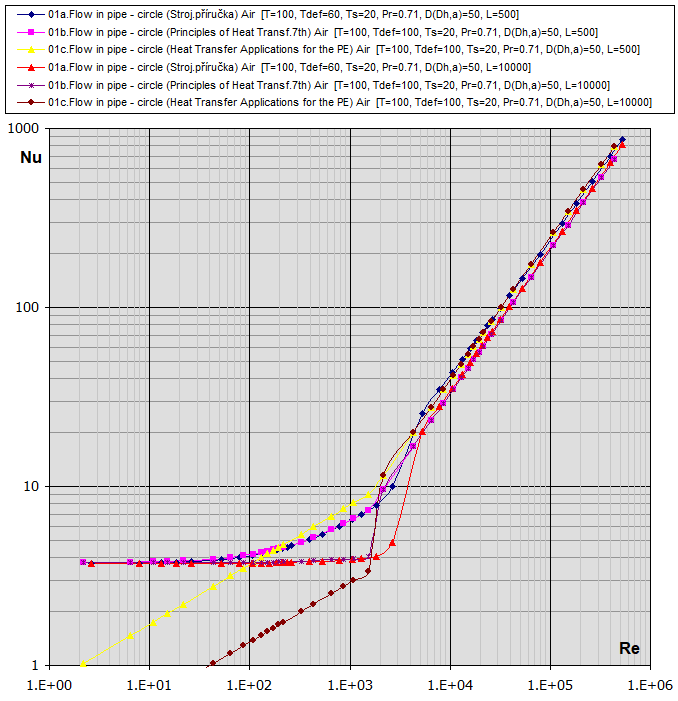
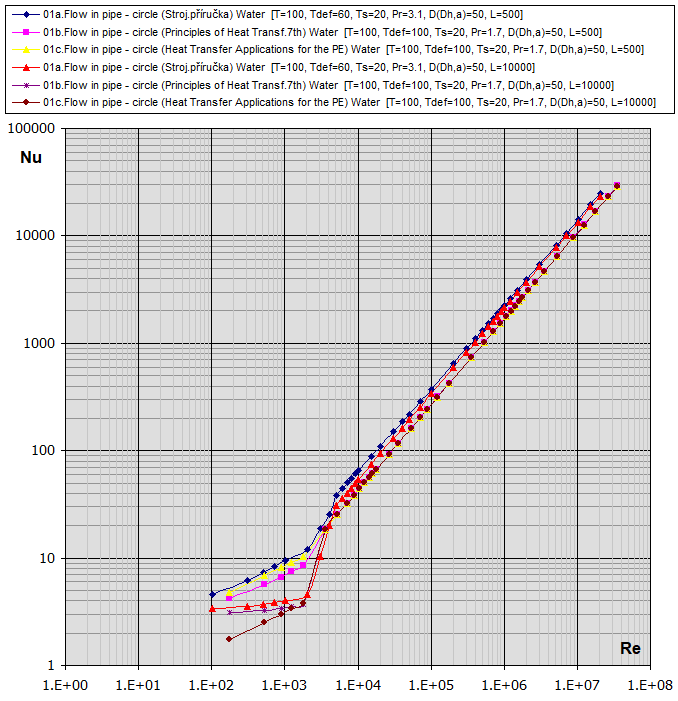

02. Proudění v potrubí - obdélník (a,b) Dh = 2 * a * b / (a + b): [Tdef =
(T+Ts)/2, 0.1<Re<1e7] ...
(Strojírenská příručka)
03.
Proudění v potrubí -
čtverec (a) Dh = a: [Tdef = (T+Ts)/2, 0.1<Re<1e7]
... (Strojírenská příručka)
04.
Proudění v potrubí -
šestihran (a) Dh = a: [Tdef = (T+Ts)/2, 0.1<Re<1e7] ... (Strojírenská příručka)
06.
Proudění v potrubí -
obecný profil (Ac,P) Dh = 4 * Ac / P: [Tdef = (T+Ts)/2,
0.1<Re<1e7] ...
(Strojírenská příručka)
hc = (Nu *
λ) / Dh
Nu = (3.65 + (0.0668 * Re * Pr * (Dh/L)) / (1 + 0.045 * (Re * Pr *
(Dh/L))^(2/3))) * (μ / μs)^0.14 .... [Re<2300]
Nu = 0.037*(1 + (Dh/L)^(2/3)) * (Re^0.75 - 180) * Pr^0.42 .... [Re>2300]
05. Proudění v potrubí - mezikruží (d1,d2) Dh = d1 - d2: [Tdef = (T+Ts)/2, 0.1<Re<1e7] ... (Gnielinski)
hc = (Nu * λ) / Dh
Laminární proudění [Re<2300] aproximací z tabulky:
| Diameter ratio | NuL1 | NuL2 |
| d2/d1 | (inside) | (outside) |
| 0.00 (tube) | - | 4.36 |
| 0.05 | 17.46 | 4.79 |
| 0.1 | 11.56 | 4.86 |
| 0.25 | 8.24 | 5.1 |
| 0.5 | 6.49 | 5.47 |
| 1.00 (planar slot) | 5.39 | 5.39 |
Turbulentní proudění [Re>4000]:
Pro vnitřní kružnici
NuT1=(0.86*(y)^(-0.16)) * NuS1
Pro vnější kružnici
NuT2=(1 - ((1 - 0.86*(y)^0.16) / (3 * (y)))) * NuS2
y = d2 / d1 ... Poměr průměrů
NuS = ((f / 8) * (Re - 1000) * Pr) / (1 + 12.7 * (f / 8)^0.5 * (Pr^(2/3) - 1))
f = (1.82 * log(Re) - 1.64)^(-2)
Proudění v přechodové oblasti (2300<Re<4000):
Lineární interpolace z NuL a NuT
NuP = (1 - (Re - 2300)/1700) * NuL + ((Re - 2300)/1700) * NuT
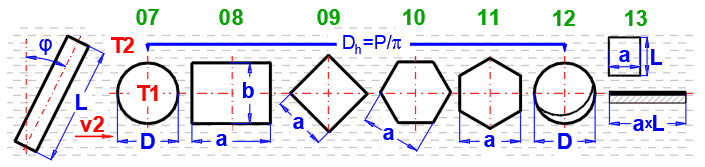
fcoeff ... Šikmé obtékání potrubí
| φ | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° |
| fcoeff | 1.00 | 1.00 | 0.99 | 0.95 | 0.86 | 0.75 | 0.63 | 0.50 |
07a. Obtékání
trubky - válec (D): [Tdef = (T+Ts)/2, 0.5<Pr<1e3, 0.4<Re<4e5] ...
(Strojírenská příručka)
hc = (Nu *
λ) / D
* fcoeff
Nu =1.11 * K * Re^m * Pr^0.31
Nu =1.11 * K * Re^m * Pr^0.31 * (0.785 * (Ts/T)^(m/4) ..... for Gas
| Re | K | m |
| 0.4<Re<4 | 0.891 | 0.33 |
| 4<Re<40 | 0.821 | 0.385 |
| 40<Re<4e3 | 0.615 | 0.466 |
| 4e3<Re<4e4 | 0.174 | 0.618 |
| 4e4<Re<4e5 | 0.0239 | 0.805 |
07b.
Obtékání trubky - válec (D): [Tdef =
T, 0.5<Pr<1e3,
0<Re<1e6] ...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D
* fcoeff
Nu =C * Re^m * Pr^n * (Pr/Prs)^0.25
n = 0.37 [Pr<10]
n= 0.36 [Pr>10]
| Re | C | m |
| Re<40 | 0.75 | 0.4 |
| 40<Re<1e3 | 0.51 | 0.5 |
| 1e3<Re<2e5 | 0.26 | 0.6 |
| 2e5<Re<1e6 | 0.076 | 0.7 |
07c.
Obtékání trubky - válec
(D): [Tdef = (T+Ts)/2, 0.5<Pr<1e3, 0.04<Re<4e5] ...
(Heat Transfer Applications
for the Practicing Engineer)
hc = (Nu *
λ) / D
* fcoeff
Nu = C * Re^m * Pr^0.3333
| Re | C | m |
| 0.04<Re<4 | 0.989 | 0.33 |
| 4<Re<40 | 0.911 | 0.385 |
| 40<Re<4e3 | 0.683 | 0.466 |
| 4e3<Re<4e4 | 0.193 | 0.618 |
| 4e4<Re<4e5 | 0.027 | 0.805 |
Re-Nu graf pro
vzduch a vodu (T
... [°C], D,Dh,L ... [mm])
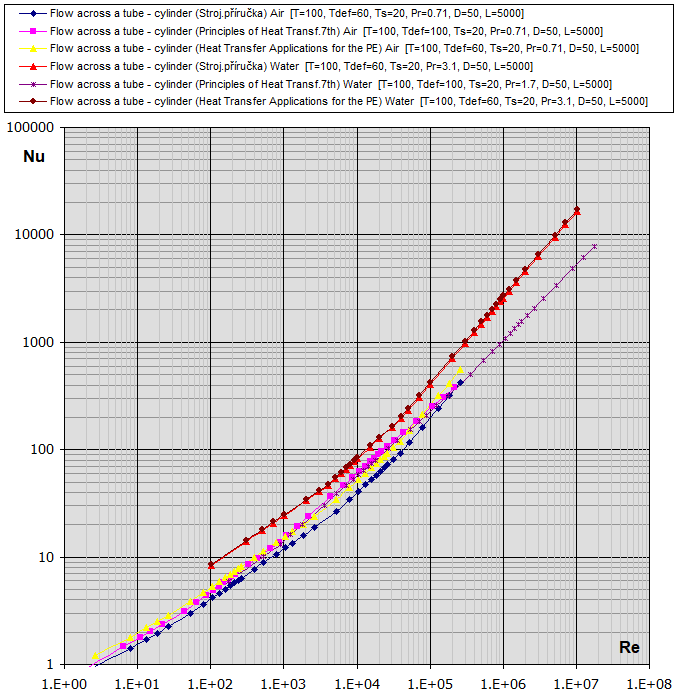

fcoeff ... Šikmé obtékání potrubí
| φ | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° |
| fcoeff | 1.00 | 1.00 | 0.99 | 0.95 | 0.86 | 0.75 | 0.63 | 0.50 |
08a. Obtékání trubky
- čtverec (a):
[Tdef = (T+Ts)/2, 5e3<Re<1e5,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =4
* a / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ) / Dh
* fcoeff
Nu =1.11 *
0.0921 * Re^0.675 * Pr^0.31
Nu =1.11 * 0.0921 * Re^0.675 * Pr^0.31 * (0.785 * (Ts/T)^(0.675/4) ..... for Gas
08b. Obtékání trubky - čtverec (a):
[Tdef = T, 2.5e3<Re<1e5,
0.6<Pr<0.85] ...
(Principles of Heat Transfer
7th. edtion)
Dh = a
Re =(a * v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu =
0.16
*
Re^0.699
... [2.5e3<Re<8e3]
Nu = 0.092 * Re^0.675 ... [5e3<Re<1e5]
08c. Obtékání trubky - obdélník (a,b):
[Tdef
= (T+Ts)/2, 2.5e3<Re<1e5, 0.5<Pr<1e3,
0.5<a/b<1] ...
(Principles of Heat Transfer
7th. edtion)
Dh =2
* (a + b) / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu = 0.104 *
Pr^0.35 *
Re^0.675
..... [a/b=1]
Nu
= 0.264
* Pr^0.35 *
Re^0.66
...... [a/b=0.5]
Re-Nu-hc graf pro vzduch a vodu (T ... [°C], D,Dh,L ... [mm])
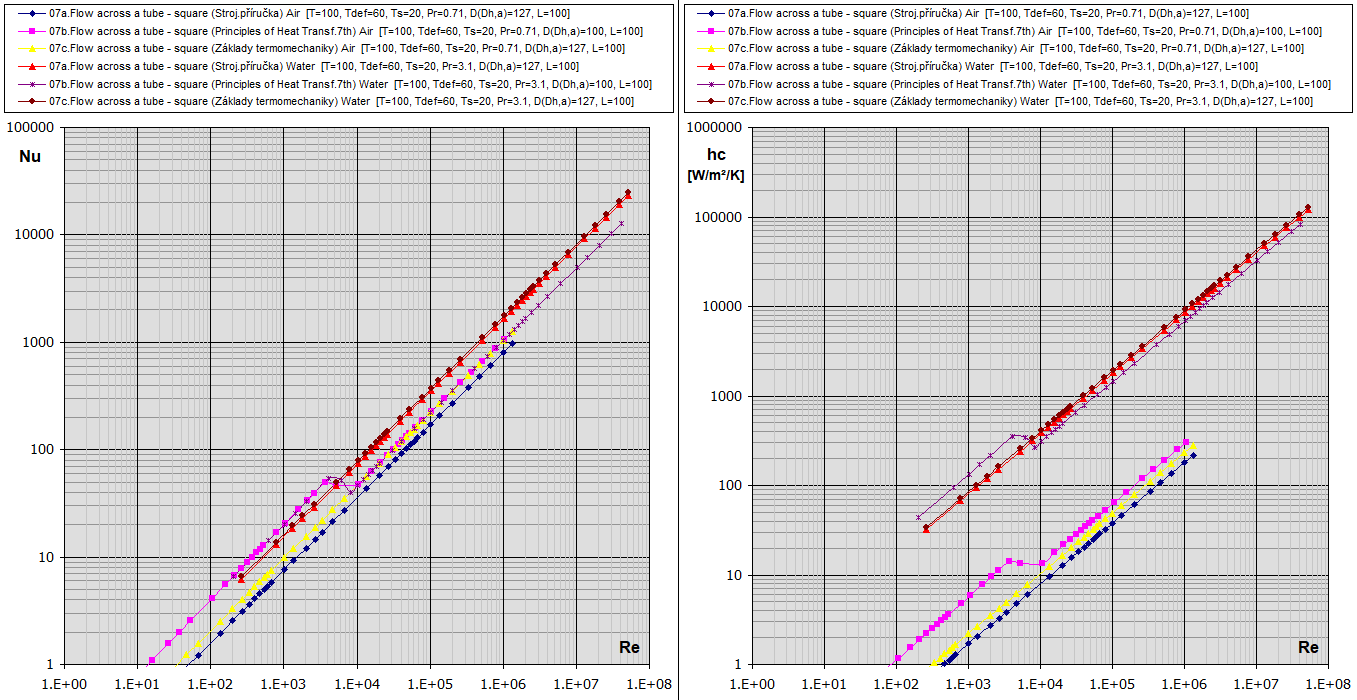
09a.
Obtékání trubky - čtverec (a):
[Tdef = (T+Ts)/2, 5e3<Re<1e5,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =4 * a / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ) / Dh
* fcoeff
Nu =1.11 *
0.222 * Re^0.588 * Pr^0.31
Nu =1.11 * 0.222 * Re^0.588
* Pr^0.31 * (0.785 * (Ts/T)^(0.588/4) ..... for Gas
09b.
Obtékání trubky - čtverec (a):
[Tdef = T, 2.5e3<Re<1e5,
0.6<Pr<0.85] ...
(Principles of Heat Transfer
7th. edtion)
x = (2 *
a^2)^0.5
Re =(x *
v) / KinVis
hc = (Nu *
λ)
/ x
* fcoeff
Nu =
0.261*
Re^0.624 ... [2.5e3<Re<7.5e3]
Nu = 0.222 * Re^0.588 ... [5e3<Re<1e5]
10a. Obtékání trubky
- šestiúhelník (a):
[Tdef = (T+Ts)/2, 5e3<Re<1e5,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =6 * a / (3^0.5) / 3.14
Re = (Dh * v) / KinVis
hc = (Nu *
λ) / Dh
* fcoeff
Nu =1.11 *
0.138 * Re^0.638 * Pr^0.31
Nu =1.11 * 0.138 * Re^0.638
* Pr^0.31 * (0.785 * (Ts/T)^(0.638/4) ..... for Gas
10b. Obtékání trubky - šestiúhelník (a):
[Tdef = (T+Ts)/2,
5e3<Re<1e5,
0.6<Pr<0.85] ... (Principles of Heat
Transfer
7th. edtion)
Re =(a *
v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu = 0.138 * Re^0.638
11a.
Obtékání trubky - šestiúhelník (a):
[Tdef = (T+Ts)/2, 5e3<Re<1.95e4,
0.5<Pr<1e3, 20<T<1000C] ...
(Strojírenská příručka)
Dh =6 * a / (3^0.5) / 3.14
Re = (Dh * v) / KinVis
hc = (Nu * λ) / Dh
* fcoeff
Nu =1.11 *
0.144
* Re^0.638 * Pr^0.31
Nu =1.11 * 0.144 * Re^0.638
* Pr^0.31 * (0.785 * (Ts/T)^(0.638/4) ..... for Gas
11b.
Obtékání trubky - šestiúhelník (a):
[Tdef = (T+Ts)/2, 5e3<Re<1e5, ,
0.6<Pr<0.85] ... (Principles of Heat
Transfer
7th. edtion)
x = 2 * a /
(3^0.5)
Re =(x *
v) / KinVis
hc = (Nu *
λ)
/ x
* fcoeff
Nu =
0.144
*
Re^0.638 ... [5e3<Re<1.95e4]
Nu = 0.035 * Re^0.782 ... [1.95e4<Re<1e5]
12.
Obtékání koule (D):
[Tdef = T, 3.5<Re<2e5,
0.7<Pr<380] ... (Principles
of Heat Transfer
7th. edtion)
hc = (Nu *
λ)
/ D * fcoeff
Nu =2 + (0.4 *
Re^0.5 + 0.06 * Re^(0.67)) * Pr^0.4 * (μ
/ μs)^0.25 ...
[3.5<Re<76000]
Nu =2 + (Re / 4 + 0.0003 *Re2^1.6)^0.5 ... [76000<Re<2e5]
13.
Obtékání desky φ=90° (a): [Tdef
= (T+Ts)/2, Re<1e7, 0.6<Pr<60]
... (Heat
Transfer Applications for the Practicing Engineer)
Re =(a *
v) / KinVis
hc = (Nu *
λ)
/ a
* fcoeff
Nu =
0.644
*
Re^0.5 *
Pr^0.333
... [Re<5e5,
0.6<Pr<50]
Nu = 0.037 * Re^0.8 * Pr^0.333 ... [5e5<Re<1e7,
0.6<Pr<60]
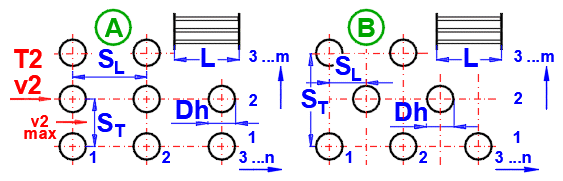
A.
Obtékání svazku trubek (D,
ST, SL, n): [Tdef = (T+Ts)/2, 0.7<Pr<500, 10<Re<200000]
...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D * A
Nu = 0.8 * Re^0.4 * Pr^0.36 * (Pr/Prs)^0.25 [10<Re<1000]
Nu = 0.27 * Re^0.63 * Pr^0.36 * (Pr/Prs)^0.25 [1000<Re<2e5, ST/SL>0.7]
Nu = 0.021 * Re^0.84 * Pr^0.36 * (Pr/Prs)^0.25 [2e5<Re]
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Coeff A |
0.68 |
0.75 |
0.83 |
0.89 |
0.92 |
0.95 |
0.97 |
0.98 |
0.99 |
1.00 |
|
Coeff B |
0.64 |
0.80 |
0.87 |
0.90 |
0.92 |
0.94 |
0.96 |
0.98 |
0.99 |
1.00 |
B.
Obtékání svazku trubek (D,
ST, SL, n): [Tdef = (T+Ts)/2, 0.7<Pr<500, 10<Re<200000]
...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ) / D * B
Nu = 0.9 * Re^0.4 * Pr^0.36 * (Pr/Prs)^0.25 [10<Re<1000]
Nu = 0.35 * (ST/SL)^0.2 * Re^0.6 * Pr^0.36 * (Pr/Prs)^0.25 [(ST/SL)<2,
1000<Re<2e5]
Nu = 0.4 * Re^0.6 * Pr^0.36 * (Pr/Prs)^0.25 [(ST/SL)>2, 1000<Re<2e5]
Nu = 0.022 * Re^0.84 * Pr^0.36 * (Pr/Prs)^0.25 [Pr>1, 2e5<Re]
Nu = 0.019 * Re^0.84 [Pr=0.7, 2e5<Re]
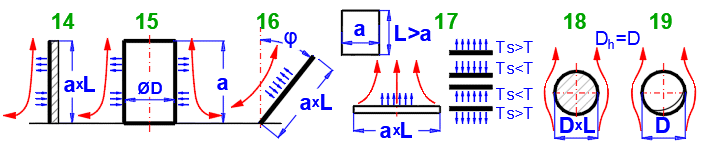
14-15.
Svislá deska nebo válec
(L): [Tdef = (T+Ts)/2, 1e3 < Ra < 1e13]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ L
Nu = 0.59 * Ra^0.25
[1e4<Ra<1e9]
Nu = 0.10 * Ra^0.333 [1e9<Ra<1e13]
16.
Nakloněná deska
(L):
[0°<φ<89.9°, Tdef = (T+Ts)/2, 1e3 < Ra < 1e13]
...
(Principles of Heat Transfer
7th. edtion)
hc = (Nu *
λ)
/ L
Nu = 0.59 * (Ra*cos(φ))^0.25
[1e4<Ra<1e9]
Nu = 0.10 * (Ra*cos(φ))^0.333
[1e9<Ra<1e13]
17.
Deska - horní povrch (menší
z rozměrů AxB): [Tdef = (T+Ts)/2, 2e4 < Ra < 1e11]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ L
Ts > T
Nu = 0.54 * Ra^0.25 [2e4 < Ra < 8e6]
Nu = 0.15 * Ra^0.333 [8e6 < Ra < 1e11]
Ts < T
Nu = 0.58 * Ra^0.2 [8e6 < Ra < 1e11]
17.
Deska - spodní povrch
(menší z rozměrů AxB): [Tdef = (T+Ts)/2, 2e4 < Ra < 1e11]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ L
Ts < T
Nu = 0.54 * Ra^0.25 [2e4 < Ra < 8e6]
Nu = 0.15 * Ra^0.333 [8e6 < Ra < 1e11]
Ts > T
Nu = 0.58 * Ra^0.2 [8e6 < Ra < 1e11]
18.
Vodorovný válec (D): [Tdef
= (T+Ts)/2, 1e-5 < Ra < 1e12] ...
(Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ D
Nu = 0.4 * Ra^0 [0 < Ra < 1e-5]
Nu = 0.85 * Ra^0.188 [1e-5 < Ra < 1e4]
Nu = 0.53 * Ra^0.25 [1e4 < Ra < 1e9]
Nu = 0.13 * Ra^0.333 [1e9 < Ra < 1e12]
19. Koule (D): [Tdef = (T+Ts)/2, 1e-5 < Ra < 1e12]
... (Heat Transfer Applications for the Practicing Engineer)
hc = (Nu *
λ)
/ D
Nu1=0.6 * Ra^0.25
Nu2=2 + (0.589 * Ra^0.25) / (1 + (0.469 / Gr^(9/16)))^(4/9)
Nu=(Nu1 + Nu2) / 2
Pro zvýšení přestupu tepla (zvýšení teplosměnné plochy) se používá žebrování
(chladiče v počítačích, vytápění, výměníky tepla...).
Nejjednodušší (orientační) typ výpočtu bere v úvahu pouze celou plochu
žebrovaného povrchu a součinitel přestupu tepla hc vztažený k povrchu bez žeber.
Vztahy použité v tomto výpočtu zohledňují i další parametry (tvar a rozměry žebra).
Výsledkem výpočtu žebrování je celková teplosměnná plocha At a celková účinnost
žebrování ηof.
Pro výpočet měrného tepelného toku prouděním qc' je
pak použit upravený vztah:
qc' = hc * (T - Ts) * ηof
a pro výpočet celkového tepelného toku prouděním Qc vztah:
Qc = qc' * At
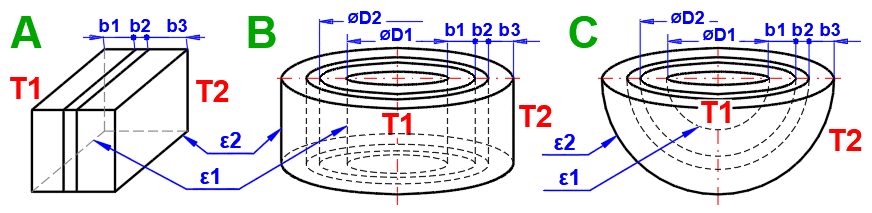
Tvary žebrování a obtékání žeber řešené v této aplikaci.
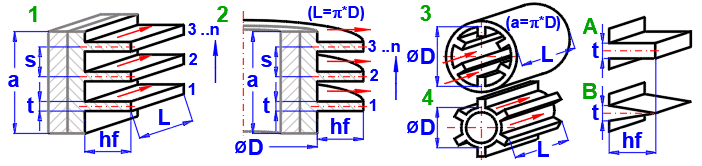
1A) Přímá žebra - obdélníková
Af = 2 * hfc * L [m²]
hfc = hf + (t/2) [m]
Ap = t * hf [m²]
1B) Přímá žebra - trojúhelníková
Af = 2 * L * (hf^2 + (t/2)^2)^0.5 [m²]
Ap = (t /2) * hf
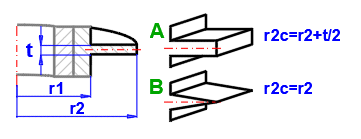
2A) Kruhová žebra - obdélníková
Af = (3.1416 * (D/2 + hfc)^2 - 3.1416 * (D/2)^2) * 2
hfc = hf + (t/2) [m]
Ap = t * hf [m²]
2B) Kruhová žebra - trojúhelníková
Af = (3.1416 * (D/2 + hfc)^2 - 3.1416 * (D/2)^2) * 2
hfc = (hf^2 + (t / 2.3)^2)^0.5)
Ap = (t /2) * hf
Af ... Plocha žebra
hf ... Výška žebra
hfc ... Korigovaná výška žebra
Ap ... Plocha řezu žebrem
x-ová souřadnice grafu je bezrozměrná hodnota
x = hfc^(3/2) * (hc / (Lambda * Ap))^(1/2)
hc ... Součinitel prostupu tepla [W/m²/K]
Lambda ... Součinitel tepelné vodivosti materiálu žeber [W/(m.K)]
y-ová souřadnice grafu je účinnost žebra
ηf ... Účinnost žebra
Účinnost přímých žeber obdélníkového, trojúhelníkového a parabolického profilu.
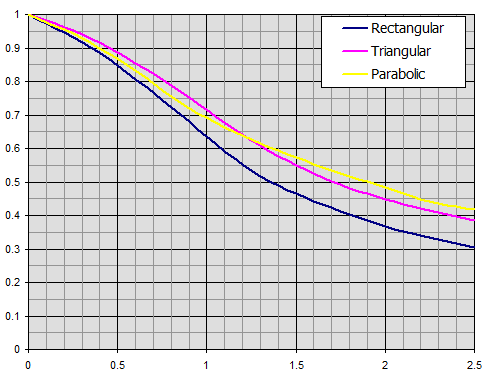
Účinnost kruhových žeber o konstantní tloušťce t.
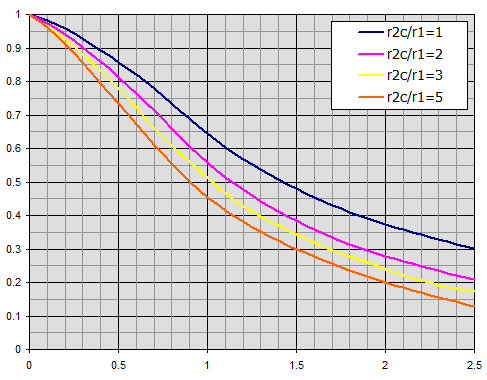
Jednotlivé křivky jsou vztažené na poměr poloměrů r2c/r1
ηof = (1 - (n * Af) / At * (1 - ηf))
n ... Počet žeber
Af ... Plocha žebra
At ... Celková plocha
ηf ... Účinnost žebra
Zářivá energie je přenášena elektromagnetickým zářením o různé vlnové délce. Problematika přestupu tepla zářením je poměrně složitá, proto jsou řešené pouze základní, v běžné strojírenské praxi, používané úlohy.

Ve vzorcích je použito značení podle obrázku.
hr = ɛ * δ0 * (Ts^4 - Tsky^4) / (Ts - Tsky)
ε ... Emisivita stěny [0...1]
δ0 ... Stefan-Bolzmannova konstanta
δ0 = 5.67e-8 [W/m²/K⁴]
Ts ...
Teplota stěny [°K]
Tsky ...
Teplota prostoru [°K]
Q1 = ε1 * δ0 * A1 * (T1K^4 - Tsky^4)
ε1 ... Emisivita stěny [0...1]
δ0 ... Stefan-Bolzmannova konstanta
δ0 = 5.67e-8 [W/m²/K⁴]
Tsky ... Teplota prostoru [°K]
T1K ... Teplota stěny [°K]
q1 = Q1 / A1
A1 ... Plocha stěny [m²]
Q12 = (δ0 * A1 * (T1K^4 - T2K^4)) / (1/ε1 + A1/A2 * (1/ε2 - 1))
ε1 ... Emisivita stěny 1 [0...1]
ε2 ... Emisivita stěny 2 [0...1]
A1 ... Plocha stěny 1 [m²]
A2 ... Plocha stěny 2 [m²]
T1K ... Teplota stěny 1 [°K]
T1K ... Teplota stěny 2 [°K]
q12 = Q12 / A1
A1 ... Plocha stěny 1 [m²]
Q12 =(δ0 * (T1K^4 - T2K^4)) / ((1 - ε1) / (ε1 * A1) + (1 - ε3) / (ε3 * Ax) + (1 - ε4) / (ε4 * Ax) + (1 - ε2) / (ε2 * A2))
ε3 ... Emisivita stínící fólie x [0...1]
ε4 ... Emisivita stínící fólie x [0...1]
Ax ... Plocha stínící fólie x [m²]
q12 = Q12 / A1
A1 ... Plocha stěny 1 [m²]
Tx = ((R1 * T2K^4 + R2 * T1K^4) / (R1 + R2))^0.25
R1 ... Odpor mezi 1 a x
R2 ... Odpor mezi x a 2
R1 = (1 - ε1) / (ε1 * A1) + (1-ε3) / (ε3 * Ax)
R2 = (1 - ε4) / (ε4 * Ax) + (1 - ε2) / (ε2 * A2)
Q12 = (δ0 * (T1K^4 - T2K^4)) / Rsum
Rsum = R1 + R2 + R3
R1 = (1 - ε1) / (ε1 * A1) + (1 - ε3) / (ε3 * Ax)
R2 = (1 - ε4) / (ε4 * Ax) + (1 - ε5) / (ε5 * Ay)
R3 =(1 - ε6) / (ε6 * Ay) + (1 - ε2) / (ε2 * A2)
R1 ... Odpor mezi 1 a x
R2 ... Odpor mezi x a y
R3 ... Odpor mezi y a 2
q12 = Q12 / A1
A1 ... Plocha stěny 1 [m²]
Tx = (T1K^4 - Q12 * R1 / δ0)^0.25
Ty = (T2K^4 + Q12 * R3 / δ0)^0.25
Výpočet není jednoduše a přímo řešitelný. Tepelný tok je závislý na celé řadě parametrů (teploty, vlastnosti kapaliny, materiál stěny, geometrie...), které se mění s teplotou stěny.
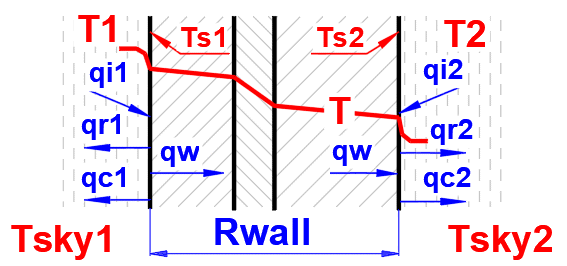
Pro
řešení teploty stěny Ts1 a Ts2 je použita rovnice tepelného toku pro
zadané parametry kapaliny a stěny. Postupně
se zpřesňují teploty Ts1 a Ts2 tak, aby vyhovovaly rovnicím:
Ts2 = Ts1 - q1 * Rwall, Q1 = -Q2
Q1 = (qi1 + qr1 + qc1) * A1
Q2 = (qi2 + qr2 + qc2) * A2
Q1 ...
Celkový tepelný tok levé strany [W]
Q2 ... Celkový tepelný tok pravé strany
[W]
Pro výpočet tepelného toku q jsou použité
následující vztahy (viz předchozí odstavce):
qc = hc * (T - Ts) ... f (T, Ts, p, Rho, μ, Cp, λ.....)
qr = hr * (T - Ts) ... f (T, Ts, ε.....)
qi ... vstupní parametr - přímé ozařování (slunce, externí zdroj tepla....)
Vyřešení teploty stěny Ts1 a Ts2 vede samozřejmě k tomu, že se změní hodnoty hc1, hc2, hr1, hr2.
Proto je možné spustit ručně druhou iteraci, při které jsou několikrát po sobě použity nové hodnoty hc1 a hc2 pro další zpřesnění výsledků.
Řešení teplot Ts1 and Ts2:
První odhad (n=1):
Ts1K[°K] = 100
*
(ABS((T1K
/
100)^4 - qi1
/ c0'))^0.25
Ts2K[°K] =
Ts1K - q1 * Rwall
qc1[W/m²] =
(T1K
-
Ts1K)
*
hc1
*
FinEff1
qc2[W/m²] = (Ts2K - T2K) * hc2
*
FinEff2
qr1[W/m²] =
(Tsky1
-
Ts1K)
*
hr1
qr2[W/m²] = (Ts2K - Tsky2) * hr2
q1[W/m²] = qi1 + qc1 + qr1
q2[W/m²] = qi2 + qc2 + qr2
ΔQ[W] =
Q1
-
Q2 = (q1 * A1 - q2 * A2) /
A2
ΔTs2 =IF(ABS(ΔQ)
> 1;(ΔQ/ABS(ΔQ)*(ABS(ΔQ)^0.5));ΔQ/2)
Aproximace (100 kroků, metoda polovičního intervalu, n = 2...100)
Ts1K(n) = Ts1K(n-1) + ΔTs2(n-1)
Ts2K(n) = Ts1K(n) - q1 * Rwall
qc1(n) = (T1K
-
Ts1K(n))
*
hc1
*
FinEff1
qc2(n) = (Ts2K(n) - T2K) * hc2
*
FinEff2
qr1 =
(Tsky1
-
Ts1K(n))
*
hr1
qr2 = (Ts2K(n) - Tsky2) *
hr2
qw(n) =
1
/
Rwall
*
(Ts2K(n)
- Ts1K(n))
q1(n) = qi1 + qc1(n) + qr1(n)
q2(n) = qi2 + qc2(n) + qr2(n)
ΔQ(n) =
Q1(n)
-
Q2(n) = (q1(n) * A1 - q2(n)
* A2) / A2
ΔTs2(n) = IF(ΔQ(n-1)*ΔQ(n) < 0; ΔTs2(n-1)/-2; ΔTs2(n-1))
kde:
c0' = δ0 * 1e8
= 5.67
δ0
=
5.67e-8
...
Konstanta záření dokonale černého tělesa
[W/m²/K⁴]
Rwall ... Tepelný odpor stěny [m²K/W]
Tsky ...
Teplota prostoru [°K]
FinEff ... Účinnost žebrování [0 ... 1]
Pro získání přesné hodnoty podélné změny teploty v potrubí s proudící látkou (kapalina, plyn) platí rovnice:
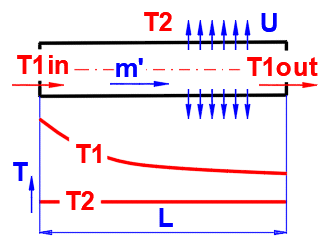
dTL = ABS(T1in - T2) * EXP(-Alpha * L)
T1in ... Teplota látky na vstupu [°C]
T2 ... Teplota okolí [°C]
L ... Vzdálenost od vstupu [m]
Alpha = U / (m' * Cp)
U … Lineární součinitel přestupu tepla [W/m/K]
m' ... Hmotnostní průtok látky [kg/s]
Cp … Měrná tepelná kapacita latky [J/kg/K]
T1out =
T2 + dTL ...
(T1in>T2)
T1out = T2 - dTL .... (T1in<T2)
T1out ... Výstupní teplota (teplota ve vzdálenosti L od vstupu) [°C]
Výkon / Příkon
Pw = -m' * Cp * (T1in - T1out) [W]
Doba ochlazování neřeší fázové změny látky.
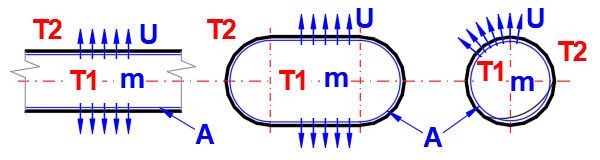
Phi = U * A * (1Ts - T2)
U … Plošný součinitel přestupu tepla [W/m²/K]
A … Vnitřní plocha potrubí, zásobníku [m²]
T1s … Počáteční teplota média uvnitř [°C]
T2 … Okolní teplota [°C]
Time = ((T1s - T2) * m * Cp * LN((T1s - T2) / (T1e - T2)) / Phi
m ... Hmotnost látky [kg]
Cp … Měrná tepelná kapacita látky [J/kg/K]
T1e … Koncová teplota média uvnitř [°C]
Základní typ výměníku tepla
- souproudý výměník tepla
- protiproudý výměník tepla
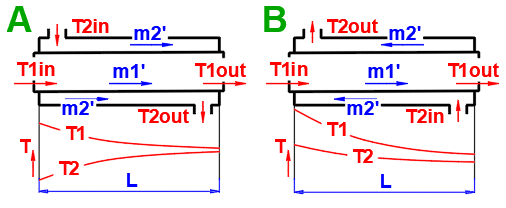
Odvozené typy výměníků.
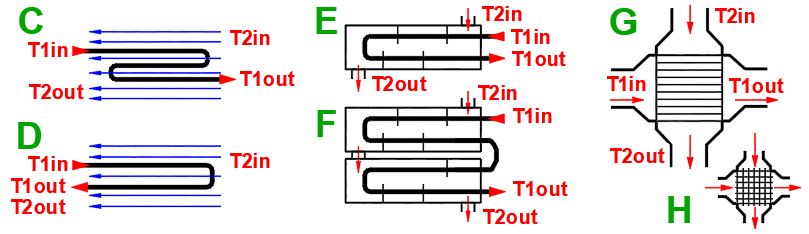
Q1 = m1'
*
Cp1
*
dT1
Q2 = m2'
*
Cp2
*
dT2
m1', m2' ... Hmotnostní tok [kg/s]
Cp1, Cp2 ... Měrná tepelná kapacita [J/kg/°K]
dT1, dT2 ... Teplotní rozdíl [°C]
Souproudý výměník tepla.
Protiproudý výměník tepla.
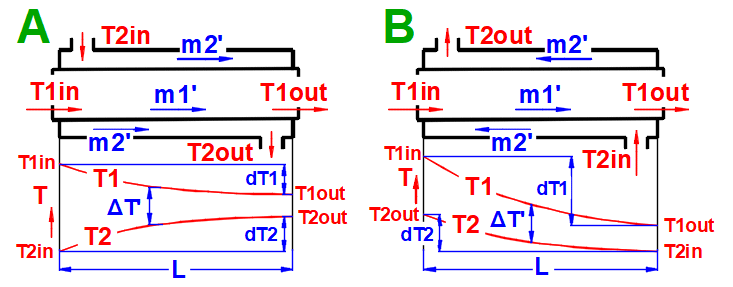
dT1 = T1Kout - T1Kin [°C]
dT2 = T2Kout - T2Kin [°C]
Souproud A:
ΔTS' = ((T1Kin - T2Kin) - (T1Kout - T2Kout)) / (LN((T1Kin
- T2Kin) / (T1Kout - T2Kout)))
Protiproud B:
ΔTP' = ((T1Kin - T2Kout) - (T1Kout - T2Kin)) /
(LN((T1Kin - T2Kout) / (T1Kout - T2Kin)))
Výměník typu C-H: ΔTX' = ΔTP' * Epsilon
T1Kin, T2Kin ... Vstupní teplota látky [°K]
T1Kout, T2Kout ... Výstupní teplota látky [°K]
Epsilon ... Korekční součinitel pro střední teplotní logaritmický rozdíl [0.5 -
1.0]
Korekční součinitel je aproximován z tabulek pomocí lineární aproximace pro výměníky C-H.
Poměr tepelné kapacity R
R = (T1Kin - T1Kout) / (T2Kout - T2Kin)
Tepelná účinnost P
P = (T2Kout - T2Kin) / (T1Kin - T2Kin)
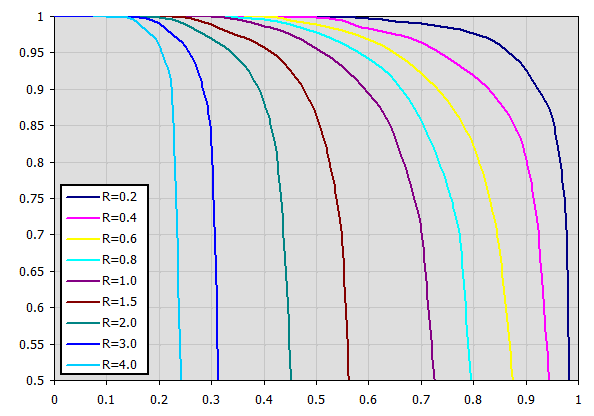
Odpovídající grafy pro Epsilon pro mnoho typů výměníků jsou dostupné v uvedené literatuře.
Příklad grafu (aproximace z tabulky) pro výměník typu F. (Xaxis ... P, Yaxis ... Epsilon)
P=0.7, R=0.8 => Epsilon=0.85
A = ABS(Q1 / (Upl * ΔT'))
Q1,Q2 ... Tepelný tok Q1,Q2 [W], podmínka: Q1 = -Q2
ΔT' ... Střední logaritmický teplotní rozdíl (ΔTS',
ΔTP', ΔTX') [°C]
Upl ... Součinitel prostupu tepla - rovinná stěna [W/m²/K]
L = ABS(Q1 / (Ucyl * ΔT'))
Q1,Q2 ... Tepelný tok Q1,Q2 [W], podmínka: Q1 = -Q2
ΔT' ... Střední logaritmický teplotní rozdíl (ΔTS',
ΔTP', ΔTX') [°C]
Ucyl ... Součinitel prostupu tepla - válcová stěna [W/m/K]
Souproud A: T1Out = T1in - Theta1S
Protiproud B: T1Out = T1in - Theta1P
Výměník typu C-H: T1Out =
T1in - Theta1X
Souproud A: T2Out = T2in + Theta2S
Protiproud B: T2Out = T2in + Theta2P
Výměník typu C-H: T2Out =
T2in - Theta2X
Theta1S = (T1Kin - T2Kin) * FiS
Theta1P = (T1Kin - T2Kin) * FiP
Theta1X = (T1Kin - T2Kin) * FiX
Theta2S = C1 / C2 * Theta1S
Theta2P = C1 / C2 * Theta1P
Theta2X = C1 / C2 * Theta1X
C1 = m1'
*
Cp1
C2 = m2'
*
Cp2
Souproud A: FiS = (1 - EXP(-U * OmegaS * LA)) / (1 + C1/C2)
Protiproud B: FiP = (1 - EXP(-U * OmegaP * LA)) / (1 - C1/C2 * EXP(-U * OmegaP *
LA))
Výměník typu C-H: FiX =
(1 -
EXP(-U * OmegaX * LA)) / (1 - C1/C2 * EXP(-U * OmegaX * LA))
LA = Areq / (1 / Epsilon)
Areq ... Zadaná plocha, pro kterou má být zjištěna výstupní teplota [m²]
Epsilon ... Korekční součinitel pro střední teplotní
logaritmický rozdíl (Výměník typu C-G) [0.5 - 1.0]
U ... Součinitel prostupu tepla - rovinná stěna [W/m²/K]
Souproud A: OmegaS = 1/C1 + 1/C2
Protiproud B:
OmegaP =1/C1 - 1/C2
Výměník typu C-H: OmegaX =1/C1 - 1/C2
Rf = 1/Ud - 1/Uc
Ud = 1/ (Rf + 1/Uc)
Rf … Koeficient znečištění [m²K/W]
Uc … Součinitel přestupu tepla čisté plochy [W/m²/K]
Řada strojírenských (stavebních) konstrukcí je vystavena slunečnímu záření. Výpočet slouží pro určení slunečního teplotního toku na plochu pro zadané podmínky (orientace plochy, datum, hodina, nadmořská výška, znečištění) a k určení celkového denního příkonu.
Použité vztahy
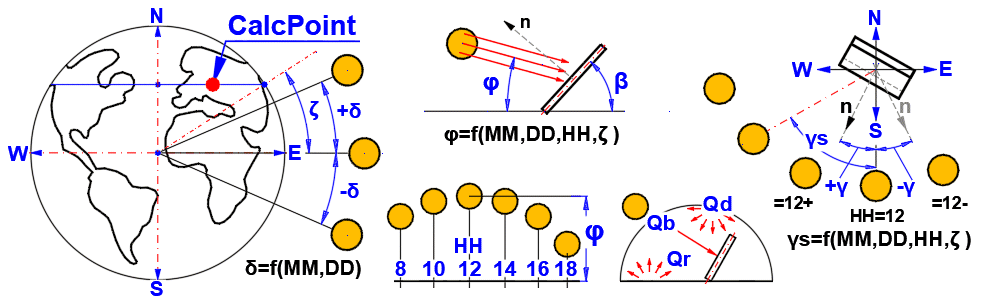
Úhly:
δ = 23.45 * SIN((360 * (284 + nn) / 365) * PI()/180)
nn ... Pořadový den v roce (1-365)
φ = ASIN((SIN(Latitude*PI()/180) * SIN(δ*PI()/180)) + (COS(Latitude*PI()/180) * COS(δ*PI()/180) * COS(15*PI()/180*(HH-12))))*180/PI()
Latitude ... Zeměpisná šířka [deg]
HH ... Hodina [0-24]
γs = ASIN(COS(δ*PI()/180) / COS(φ*PI()/180) * SIN(Tau*PI()/180))*180/PI()
Tau = 15 * (HH-12) ... Sluneční časový úhel [deg] (dopoledne (-), odpoledne (+))
θ = ACOS((SIN(φ*PI()/180) * COS(β*PI()/180) + COS(φ*PI()/180) * SIN(β*PI()/180) * COS((γs - γ)*PI()/180)))*180/PI()
β ... Sklon plochy (0-90) [deg]
γ ... Azimut plochy (+-180) [deg]
Výkon záření:
Qon =SolarConst * (1 + 0.033 * COS((360*nn/365)*PI()/180))
Sluneční zářivý tok vně atmosféry se mění v průběhu roku o +-3.3% (vzdálenost
země-slunce).
SolarConst ... Sluneční konstanta (střední hodnota 1367W/m²)
Qbn = Qon * EXP( -(Zcoeff / EpsilonCoeff))
Zcoeff ... Součinitel znečištění atmosféry (1.5 -6)
EpsilonCoeff = (9.38076 * (SIN(φ*PI()/180) + (0.003 + SIN(φ*PI()/180)^2)^0.5)) /
(2.0015 * (1-Lv*10^-4))+0.91018
Lv ... Nadmořská výška [m]
QbT = Qbn * COS(θ*PI()/180)
Qd = 0.33 * (Qon - Qbn) * SIN(φ*PI()/180)
QdT = ((1+COS(β*PI()/180))/2) * Qd
QrT = Rhog * ((1 - COS(β*PI()/180))/2) * (Qb + Qd)
Qb = QbT * SIN(φ*PI()/180) / COS(θ*PI()/180)
Rhog ... Poměr mezi odraženou a dopadlou hustotou slunečního zářivého toku
(0-1).
QT' = QbT + QdT + QrT
QT = As * QT'
As ... Celková ozařovaná plocha
Q = QT * Efficiency / 100
Efficiency ... Účinnost přeměny slunečního záření na využitelnou energii (0-100).
Pro výpočet Pw je zjištěna hodnota Q v čase t=0-24h po 30 minutách. Tyto hodnoty jsou pak sečtené do celkové Pw.
Pw = Sum (Q(t) * 0.5) [t=0-24]
Výpočty pokrývají některé často řešené úlohy z oblasti termomechaniky. Jelikož řešené úlohy spolu souvisí volně, není zde uveden žádný univerzální postup. Postupy se liší na základě řešeného problému a pokud vaše úloha spadá do okruhu řešených problémů, doporučujeme studium příkladů, které jsou zařazené v nápovědě. Pro každý typ výpočtu je většinou zařazeno několik typových úloh, které vás seznámí s konkrétním postupem.
V tomto odstavci nastavíte jednotky výpočtu.
Ve výběrovém seznamu vyberte požadovanou soustavu jednotek výpočtu. Při přepnutí jednotek budou okamžitě změněny všechny hodnoty.
Do vstupního políčka na levé straně zadejte hodnotu, kterou chcete převést. Zvolte zdrojové jednotky a na pravé straně zvolte cílové jednotky.
V odstavci jsou jednoduché výpočty energií (ohřátí, ochlazení, změna skupenství, spalování). Pokud není uvedeno jinak, jsou koeficienty v tabulkách uváděné pro teplotu 20C a tlak 0.1MPa.
Pro ohřátí / ochlazení látky je nutné dodat / odebrat energii.
Zvolte skupinu materiálů. Ukazatel v tabulce materiálů (následující řádek) bude nastaven na první materiál odpovídajícího typu.
Vyberte materiál.
Informační hodnoty, nemají žádný vliv na výpočet.
V zeleném poli je hodnota Cp pro vybraný materiál. Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
Zadejte hmotnost ohřívaného / ochlazovaného materiálu.
Přepínač vpravo určuje, která hodnota se má spočítat.
Zadejte změnu teploty.
Energie vynaložená pro změnu teploty.
Při změně skupenství (pevná látka -> kapalina -> plyn) je nutné dodat / odebrat energii.
Vyberte materiál. V hranatých závorkách je uvedena teplota tání [TM] a teplota varu [TB].
V zeleném poli jsou hodnoty CpM, CpB materiálu vybraného ze seznamu. Po odškrtnutí tlačítka můžete zadat vlastní hodnoty.
Zadejte hmotnost média. Po zaškrtnutí tlačítka je použita hodnota z předchozího výpočtu.
Energie vynaložená / získaná při změně skupenství.
Spalné teplo
(Higher Heating Value - HHV) je množství tepla, které se uvolní při izobarickém spálení 1 molu sloučeniny v plynném kyslíku na konečné oxidační produkty. Předpokládá se, že voda, uvolněná spalováním, zkondenzuje a energii chemické reakce není třeba redukovat o její skupenské teplo.
Výhřevnost
U výhřevnosti (Lower Heating Value - LHV) se předpokládá na konci reakce voda v plynném skupenství.
Proto je hodnota spalného tepla HHV vždy větší nebo rovna hodnotě výhřevnosti LHV. Rovnost nastává, když spalováním nevzniká voda.
Vyberte spalovaný materiál ze seznamu.
U výhřevnosti (Lower Heating Value - LHV) se předpokládá na konci reakce voda v plynném skupenství.
Spalné teplo (HHV) - hodnota je přesná pro spalování definovaných sloučenin (H2, CH4O....).
Pro paliva, která obsahují různé směsi (uhlí, ropné produkty, zemní plyn...) jsou běžné hodnoty nižší/vyšší od tabulkové hodnoty. V zeleném poli je udaný odhadnutý rozptyl od tabulkových hodnot.
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu HHV.
Zadejte hmotnost spáleného materiálu.
Účinnost spalování udává, kolik energie z paliva je přeneseno do nosného média.
Plynové kotle:
Kondenzační kotle .... až 98 %
Nízkoteplotní kotle .... do 89 %
Klasické kotle .... do 84 %
Kotle na tuhá paliva:
Zplynovací kotle na dřevo nebo dřevěné pelety .... až 92 %
Automatické kotle na uhlí .... 80 až 90 %
Kotle na uhlí a jiná tuhá paliva ... přes 70 %
Energie získaná spálením paliva.
V odstavci je periodická tabulka prvků, výpočet Molární hmotnosti a Poissonovy konstanty pro prvky, sloučeniny a jejich směsi. Ve druhé části je výpočet stavu a změny stavu ideálního plynu (pV=mrT).
Zadejte souhrnný chemický vzorec sloučeniny. Po stisknutí tlačíka ">>" je vzorec rozebrán na jednotlivé prvky a odpovídající seznam je vyplněn níže. Pokud chcete řešit směs sloučenin, oddělte je znakem "+". Při čtení vzorce je doplněno pořadové číslo sloučeniny (prvku) ve směsi v posledním sloupci tabulky.
Příklad sloučeniny: h2so4, H2O, cO2, C4H10O, C2H3ClO2
Příklad směsi sloučenin:
Vzduch: N2+O2+Ar+CO2
Alkohol(40%)+Voda(60%): C2H5OH+H2O
Tlačítka "1-20", "21-40"... vyplní tabulku odpovídajícími prvky.
Parametry prvku vybraného ze seznamu jsou zobrazené na přslušné řádce.
Tlačítko "Clear" vyčístí 2-20 řádek.
Symbolu prvku.
Počet atomů.
Atomová hmotnost.
Molární hmotnost.
Hustota prvku.
Měrná tepelná kapacita.
Měrná tepelná kapacita tání (teplo tání).
Měrná tepelná kapacita varu (výparné teplo).
Tepelná vodivost.
Teplota tání.
Teplota varu.
Pořadové číslo sloučeniny.
Pro další výpočet parametrů směsi je nutné určit pořadové číslo sloučeniny. Jednotlivé prvky ve sloučenině tak musí mít stejné pořadové číslo.
V předchozí tabulce můžete definovat jednotlivé prvky a sloučeniny označené pořadovým číslem.
V této tabulce pak můžete po zadání hmotnostního podílu ve směsi určit celkovou Molární hmotnost směsi.
Pro ideální plyny je Poissonova konstanta určena z počtu stupňů volnosti dané molekuly.
Molární hmotnost jednotlivého prvku a nebo sloučeniny.
Zadejte hmotnostní podíl jednotlivých složek směsi. Pokud je zaškrtnuté tlačítko vpravo, jsou při vyplňování směsi ze vzorce [3.2] zachovány původní hodnoty.
Při odškrtnutém tlačítku je každé složce směsi nastavena stejná hodnota.
Červená buňka součtu na konci řádku upozorňuje na to, že součet nenít 100%.
Molární hmotnost směsi.
r = R / Msum
R .. Univerzální plynová konstanta (8314.46261815324 J/kmol/K)
Msum .. Molární hmotnost plynu
Poměr tepelných kapacit plynu při stálém tlaku a stálém objemu κ = cp / cv
Pro ideální plyny lze Poissonovu konstantu určit z počtu stupňů volnosti dané molekuly
Tlačítkem "▼M,κ▼" přenesete hodnoty M a κ do definice plynu níže.
Výpočet umožňuje řešit stav ideálního plynu (pV=mrT), změnu jeho stavu a umožňuje zjistit odpovídající energetické hodnoty (entropie, entalpie, teplo, práce...).
Po výběru (nebo definici fyzikálních parametrů) pracovního plynu můžete zjistit jeho pracovní parametry (hmotnost m, tlak p, objem V a teplotu T) na základě stavové rovnice ideálního plynu:
p * V = m * r * T
r = R / M
M = m / N
Kde:
p ... Absolutní tlak [Pa]
V ... Objem [m^3]
m ... Hmotnost [kg]
T ... Teplota [°K]
R ... Univerzální plynová konstanta R=8314.46261815324 [J/kmol/K]
M ... Molární hmotnost plynu [kg/kmol] (vzduch 28.966 kg/kmol)
N ... látkové množství [kmol]
r ... Měrná plynová konstanta [J/kg/K] (vzduch 287.0427 J/kg/K)
A … Příklad jednoduché termodynamické soustavy, ideální plyn p*V=m*r*T.
B … Vratné děje je možné popsat obecněji jako polytropické děje, kdy je tepelná kapacita (uzavřené) soustavy konstantní. Při polytropickém ději se obecně mění všechny stavové veličiny (p,V,T). Pro polytropický děj v ideálním plynu platí rovnice p*V^n = const. V diagramu p-V, T-s jsou vyznačené křivky změn pro různá n.
C ... Carnotův cyklus. Příklad ideálního tepelného stroje, který se skládá ze dvou izotermických a dvou adiabatických dějů.
D ... Křivky základních vratných stavových změn:
n=0 ,p=const, Isobaric, (dp=0, wt=0, q=Δh, w=Δh-Δu)
n=1 ,T=const, Isotermic, (dT=0, Δu=Δh=0, q=w=wt)
n=κ ,s=const, Isoentropic, (ds=0, q=0, w=-Δu, wt=-Δh)
n=∞ ,v=const, Isochoric, (dv=0, w=0, q=Δu, wt=Δu-Δh)
Vyberte pracovní plyn ze seznamu. Pokud v seznamu není, odškrtněte tlačítko vpravo a zadejte hodnty M, cp a κ.
Se změnou teploty se mění cp,cv,κ plynu. Pro předdefinované plyny můžete definovat definiční (pracovní) teplotu. V zeleném poli je doporučená hodnota (průměr z max/min hodnoty T1...T6).
Tlačítkem "◄" přenesete doporučenou hodnotu do vstupní buňky.
Pokud definujete parametry plynu zadejte hodnotu.
r = R / M
r .... měrná plynová konstanta (vzduch 287.0427 J/kg/K)
R ... Univerzální plynová konstanta (8314.46261815324 J/kmol/K)
M ... Molární hmotnost plynu (vzduch 28.996 kg/kmol)
Pokud definujete parametry plynu zadejte hodnotu.
Poměr tepelných kapacit plynu při stálém tlaku a stálém objemu κ = cp / cv.
Pro ideální plyny lze Poissonovu konstantu určit z počtu stupňů volnosti dané molekuly.
Zadejte látkové množství. Na následujcím řádku je zobrazena odpovídající hmotnost.
Po stisknutí tlačítka "◄ N1" je vyplněné látkové množství odpovídající hmotnosti m1 (bod 1).
Po stisknutí tlačítka "m1▼" je hodnota hmotnosti přesunutá do pole m1 (bod 1).
Rovnovážný stav a změna stavu ideálního plynu (Stavová rovnice).
K dspozici je 6 bodů (i=1-6). V každém bodě je možné určit rovnovážný stav plynu jeho stavovými veličinami p(i), V(i) T(i).
Pro body 2-6 je možné určit jakým způsobem došlo ke změně stavu ze stavu (i-1) do (i).
Změny stavu je možné sledovat v grafech "p-V" a "T-s".
Určení rovnovážného stavu
Zadejte postupně hodnoty, které znáte, do bílých buňek vybraného bodu. V zelených buňkách napravo jsou průběžně dopočítané honoty, které je nutné použít pro dosažení rovnovážného stavu (p*V=m*r*T). Navrženou hodnotu přesunete do bílé buňky tlačtkem "◄". Splnění rovnice signalizuje text "▼ =OK ▼". Pokud není stavová rovnice splněna, je zobrazen text "▼ Error ▼".
Stavové změny
Pokud nastavíte parametry plynu v bodě 2 (3,4...), můžete zjistit změny pro energetické hodnoty (entropie, entalpie, teplo, práce...) vzhledem k předchozímu bodu.
Doporučený postup 1:
Změna izobarická (p=konst.), izochorická (V=konst), izotermická (T=konst).
- Použijte tlačítko "►", kterým přenesete stav (m,p,V,T) do následujícího bodu.
(Tlačítko "►=" vloží do bodu odkaz na předchozí bod. Například v p2 bude "=p1", v V2 bude "=V1" atd. barva buněk bude šedivá)
- Změňte jednu vstupní hodnotu. Okamžitě jsou v zeleném sloupci navržené hodnoty pro dosažení rovnovážného stavu.
- Tlačítkem "◄" přeneste vybraný návrh do vstupní (bílé) buňky.
Doporučený postup 2:
Polytropický děj - tepelná kapacita (uzavřené) soustavy je při něm konstantní. Při polytropickém ději se obecně mění všechny stavové veličiny (p,V,T). Pro polytropický děj v ideálním plynu platí rovnice p*V^n = konst.
- Použijte tlačítko "►", kterým přenesete stav (m,p,V,T) do následujícího bodu.
- Změňte pouze jednu vstupní hodnotu (p nebo V nebo T).
- Zadejte polytropický exponent n a stisněte tlačítko "◄ Polytr.◄". Vstupní buňky jsou vyplněné hodnotami tak, aby byl dosažen požadovaný n.
Smíšení plynu - tlačítko "3 = Mix (1+2)"
Výpočet parametrů plynu který vnikne smíšením dvou částí (1+2) s různými parametry p,V,T.
m = m1 + m2
p = m / M * R * T / V
V = V1 + V2
T = (m1 * T1 + m2 * T2) / (m1 + m2)
Vratné děje je možné popsat obecněji jako politropické děje, kdy je tepelná kapacita (uzavřené) soustavy konstantní. Při polytropickém ději se obecně mění všechny stavové veličiny (p,V,T). Pro polytropický děj v ideálním plynu platí rovnice p*V^n = const.
Do vstupní buňky zadejte požadovanou hodnotu n pro přechod mezi dvěma stavy (předchozí a zadávaný). Napravo od vstupní buňky je aktuální hodnota vypočtená z p,V,T. V rozbalovacím seznamu jsou významné a často používané hodnoty.
- Použijte tlačítko "►", kterým přenesete stav (m,p,V,T) z předchozího bodu.
- Změňte pouze jednu vstupní hodnotu (p nebo V nebo T).
- Po tisknutí tlačítka "▲Polytr.▲" jsou stupní buňky vyplněné hodnotami tak, aby byl dosažen požadovaný n.
Pokud n = "?", jsou hodoty (m,p,V,T) shodné s předchozím bodem.
Pro vybrané hodnoty n pak platí:
n=0 ,p=const, Isobaric, (dp=0, wt=0, q=Δh, w=Δh-Δu)
n=1 ,T=const, Isotermic, (dT=0, Δu=Δh=0, q=w=wt)
n=κ ,s=const, Isoentropic, (ds=0, q=0, w=-Δu, wt=-Δh)
n=∞ ,v=const, Isochoric, (dv=0, w=0, q=Δu, wt=Δu-Δh)
n = ln(p2 / p1) / (ln(p2 / p1) - ln(T2 / T1))
n = (ln(V2 / V1) - ln(T2 / T1)) / ln(V2 / V1)
Typické velikosti polytropických exponentů:
Pístový kompresor: n=1,2–1,3
Proces s částečným odvodem tepla, typická hodnota pro pomalé kompresory s chlazením.
Axiální kompresor: n=1,35–1,4
Vysokorychlostní turbokompresory s minimálním odvodem tepla, blíže adiabatickému ději (γ ≈ 1,4 pro vzduch).
4-dobý benzínový motor (komprese): n=1,3–1,35
Komprese palivové směsi s částečným odvodem tepla do stěn válce.
4-dobý naftový motor (komprese): n=1,35–1,4
Vyšší kompresní poměr a komprese čistého vzduchu, menší tepelné ztráty než u benzínového motoru.
Na řádku je uvedená polytropická měrná tepelná kapacita a stav plynu:
- "▼ =OK ▼". Je dosaženo rovnovážného stavu
- "▼ Error ▼". Pokud není rovnovážný stav
Pokud cn = "?", jsou hodoty (m,p,V,T) shodné s předchozím bodem.
Tlačíítko "►►" nakopíruje hodnoty (m1,p1,V1,T1) do všech ostatních bodů.
Zadejte hmotnost pracovní látky.
Pokud je vstupní číslice červená, jedná se pouze o upozornění, že hodnota "m" v předchozím bodě je odlišná. Nemusí to být chyba!
Zadejte absolutní tlak pracovní látky.
Zadejte objem pracovní látky.
Zadejte teplotu pracovní látky.
Hodnoty pro jednotlivé body (stavy) v jedné tabulce.
Entropie
S1 = (cv * LN(T1) + r * LN(V1)) * m1
S2 = (cv * LN(T2) + r * LN(V2)) * m2
V tabulce jsou uvedené změny při přechodu ze stavu 1 do 2 (resp.2-3,3-4…). Změna stavu je zobrazena ve stavovém diagramu p-V a T-S.
Zobrazení v tabulce a v grafu zapínáte/vypínáte příslušným tlačítkem.
Sloupec označený "Sum" obsahuje součet změn.
Pokud n = "?", jsou hodoty (m,p,V,T) shodné v příslušných bodech 1-2, 2-3,....
Pro vybrané hodnoty n pak platí:
n=0 ,p=const, Isobaric, (dp=0, wt=0, q=Δh, w=Δh-Δu)
n=1 ,T=const, Isotermic, (dT=0, Δu=Δh=0, q=w=wt)
n=κ ,s=const, Isoentropic, (ds=0, q=0, w=-Δu, wt=-Δh)
n=∞ ,v=const, Isochoric, (dv=0, w=0, q=Δu, wt=Δu-Δh)
Změna entropie
ΔS = S2 - S1 = (cp * Ln(T2/T1) - r * Ln(p2 / p1))*m1
ΔS = S2 - S1 = (cv * Ln(T2/T1) + r * Ln(v2 / v1))*m1
Změna vnitřní energie
ΔU = cv*(T2 - T1) * m1
Změna entalpie
ΔH = cp * (T2 - T1) * m1
Polytropické teplo.
Přenos energie do soustavy formou tepla (Q > 0, když soustava teplo přijímá).
Q = m * cn * (T2 - T1)
Q = -((n - kappa) / (kappa - 1)) * W
Polytropická objemová práce.
Přenos energie různými formami práce (W > 0, když soustava práci koná).
W=Q-dU=m * (cn - cv) * (T2 - T1) = m * (r / (n - 1)) * (T1 - T2)
W=m * r * T1 / (n - 1) * (1 - (V1 / V2)^(n-1))
Polytropická tlaková práce (technická)
Wt = n * W
W … Polytropická objemová práce [J]
n .... Polytropicky exponent [~]
Jsou zobrazené dva nejčastěji používané stavové grafy:
Tlak (p) - Objem (V)
Teplota (T) - Entropie (S)
Číslicí je označen příslušný bod. Jednotlivé úseky je možné vypínat / zapínat tlačítky vlevo.
Komplexní řešení přestupu tepla složenou stěnou (max. 10 vrstev).
Výpočet zahrnuje:
- Přestup tepla prouděním (definice kapalin, typu proudění, definice obtékaných objektů)
- Přestup tepla vedením (definice stěny, tloušťky a materiálových parametrů jednotlivých vrstev)
- Přestupu tepla zářením (vyzařování tepla, ozařování stěny)
- Řešení svazku trubek (výměníky)
- Řešení žebrovaných povrchů
Výpočtem získáte parametry přestupu tepla "U" z media (T1) do media (T2), tepelný odpor "R", hodnoty tepelného toku a mnoho dalších.
Výpočet je variabilní a umožňuje i částečné výpočty, jako je například:
- zištění koefcientu přestupu tepla pouze mezi stěnou a médiem
- zjištění koeficientu přestupu tepla pouze samotné stěny
- řešení pro stěny ve vakuu a stěny v přímém kontaktu s topnou čí chladící plochou
Kompletní definici "stěny" je možné uložit a vytvořit si tak databázi řešení, které je možné použít v dalších kapitolách výpočtu.
Například chladnutí/ohřev potrubí a zásobníků, výpočet výměníků tepla a řešení problémů, které obsahují několik rozdílných stěn.
Postup kompletního výpočtu přestupu tepla z média 1 do média 2:
- Definujte okrajové podmínky média
- Definujte tvar a jednotlivé vrstvy stěny
- Vyberte tvar a způsob obtékání povrchu stěny pro médium 1 a 2.
- Definujte parametry přestupu tepla sáláním pro vnitřní a vnější plochu stěny
Výsledkem výpočtu je celkový koefcient přestupu tepla "U", tepelný odpor "R" a hodnoty tepelného toku.
Zadejte teplotu média uvnitř a vně.
Pro rovinné stěny teplotu vlevo a vpravo dle obrázku.
Zadejte tlak média 1 a 2.
V této části vyberte tvar stěny a definujte parametry jednotlivých vrstev.
Vyberte typ stěny.
Zvolte skupinu materiálů. Ukazatel v tabulce materiálů (následující řádek) bude nastaven na první materiál odpovídajícího typu.
Teplotní křivky ve stěně (válcová a kulová plocha) jsou nahrazeny přímkou.
x ... tloušťka stěny
y ... průběh teploty
Vyberte materiál vrstvy. Po stisknutí tlačítka "Přidat/Nahradit" je vybraný materiál přidán buď na řádek, ve kterém je aktivní buňka a nebo na první řádek bez popisu v definiční tabulce níže. Pokud již řádek obsahuje nějaké hodnoty b, ρ, λ, Cp jsou přepsány. Tlačítkem "Vymazat vše" odstraníte řádky 2-10.
V seznamu jsou uvedené jednotlivé vrstvy stěny.
Vrstva je zahrnutá do výpočtu stěny, pokud má nenulovou tloušťku.
Pokud není tabulka konzistentní (například nevyplněný řádek), je zobrazen nápis "Check". Zkontrolujte zadání.
Pokud je typ stěny válcový a nebo kulový, je nutné zadat vnitřní průměr složené stěny. Vnitřní průměry následujících vrstev jsou dopočtené ze zadané tloušťky vrstvy.
Tloušťka vrstvy stěny.
Hustota materiálu
Na výpočet přestupu tepla nemá tato hodnota vliv. Je použita při stanovení celkové hmotnosti stěny.
Tepelná vodivost
Převod jednotek
1 [W/m/K] = 0.57782 [BTU/h/ft/F]
1 [BTU/h/ft/F] = 1.7306 [W/m/K]
Měrná tepelná kapacita
Převod jednotek
1 [J/kg/°K] = 0.0002388459 [BTU/lb/°F]
1 [BTU/lb/°F] = 4186.8 [J/kg/°K]
Tepelný odpor stěny vztažený na jednotku vnitřní plochy
Převod jednotek
1 [m²K/W] = 5.6744659 [h.ft²F/Btu]
1 [h.ft²F/Btu] = 0.17622804 [m²K/W]
Thermal resistance of the wall per unit of internal area
Teplota v prvním řádku je vnitřní (levá) teplota stěny t(1).
Na dalších řádcích jsou teploty na rozhraní vrstev stěny.
Hmotnost vrstvy stěny vztažená na jednotku vnitřní plochy.
Při volbě válcové/kulové plochy je hodnota přepočítána.
V této části je řešený přestup tepla prouděním (povrch obtéká médium). Na obrázku jsou uvedené možnosti. Pro řešení je nutné definovat parametry média, typ proudění a parametry obtékaného povrchu.
A) Nucené proudění uvnitř profilu (01-06)
B) Nucené proudění okolo profilu (07-13)
C) Volné proudění - proudění vyvolané rozdílnou hustotou ohřátého/ochlazeného média (14-19)
Dále je možné řešit obtékání svazku trubek a řešit obtékání žebrovaného profilu.
Výpočet je možné použít dvěma způsoby.
A) Komplexní přestup tepla z média 1 do média 2
V tomto případě je nutné aby byl zachován řetězec výpočtu (T1=>Ts1=>Ts2=>T2). Musí být zaškrtnuté políčka na [4.14].
B) Řešení přestupu tepla mezi stěnou a médiem
Je možné po odškrtnutí [4.14] přímo zadat teplotu stěny. V tomto případě je řešený pouze přestup tepla prouděním pro danou stěnu. Platným výsledkem je pak pouze hodnota souinitele přestupu tepla hc, resp. hc+hr pro vybranou stranu stěny.
V seznamu jsou nejčastěji řešené úlohy. Výběrem ze seznamu se nastaví odpovídající typ proudění 1 a 2 a jsou zapnuté přepínače pro použití návrhových hodnot (zelené pole).
Zde definujte parametry média uvnitř a vně (vlevo a vpravo).
K dspozici jsou následující možnosti:
A - Vakum. Pokud je na straně stěny vakum a přenos tepla pomocí proudění je nulový.
B - Přímé spojení. Na straně stěny je přímo připojen zdroj tepla/chladu a dochází k přenosu tepla se ztrátami, které je možné zanedbat. Například dno hrnce na kamnech.
C - Očíslované, předdefinované, často používané kapalné a plynné látky. Pro tyto látky jsou definované vyžadované parametry v závislosti na teplotě (tlaku).
Pokud není kapalina / plyn v seznamu, odškrtněte tlačítko na řádku s hodnotou hustoty a zadejte ručně všechny parametry kapaliny / plynu pro definiční teplotu Tdef.
V zeleném poli je hodnota, která je výsledkem kompletního výpočtu přestupu tepla z média 1 do média 2 (záření, proudění => vedení => proudění, záření). Tato hodnota je získána postupnou iterací teploty stěny tak, aby byl shodný teplotní tok Q1 a Q2.
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
V tom případě je pak výsledkem výpočtu přestup tepla záření+proudění na příslušné straně stěny.
Kriteriální rovnice pro výpočet přestupu tepla hc od různých autorů používají pro definici parametrů kapaliny / plynu různé teploty.
a) průměrná teplota filmu u stěny Tdef = (T + Ts)/2
b) střední teplotu Tdef = T
U většiny rovnic je použita Tdef = (T + Ts)/2.
Pokud není zvoleno přímé zadání hodnoty (první volba), je při volbě kriteriální rovnice [4.23] provedeno automatické přepnutí.
Dynamická viskozita pro teplotu stěny Ts
Dynamická viskozita pro definiční teplotu Tdef
Vyberte typ proudění. V seznamu znamená první písmeno:
A-Nucená konvekce
B-Volná konvekce
Číslo odpovídá obrázku nahoře a malé písmeno za číslem určuje rovnici (zdroj), která je použita.
Vyberte typ proudění pro médium 1 a médium 2, odpovídající vaší úloze podle obrázku nahoře. Vzájemná kombinace výběru by měla dávat smysl. Například není možné aby médium 1 proudilo v trubce s kruhovým průřezem a médium 2 obtékalo kouli.
Na nevhodnou kombinaci upozorní červený nápis "Check" mezi výběrovými seznamy.
**) Proudění mezikružím 05
Pokud je tato volba (05) vybrána jako vnitřní (levá) stěna, je řešený přestup tepla pro vnější průměr d1 (mezi proudící kapalinou a vnějškem).
Pokud je tato voba (05) vybrána jako vnější (pravá) stěna, je řešený přestup tepla pro vnitřní průměr d2 (mezi proudící kapalinou a vnitřkem).
Povolená kombinace je tak:
1) A-05 ... A-07 a nebo
2) A-01 ... A-05 (vhodné, pokud chcete použít podélná žebra pro vnější povrch trubky)
Pokud je vybrán typ proudění A-Forced convection zadejte rychlost proudění.
Po výběru typu proudění se nastaví odpovídajícím způsobem názvy proměnných podle obrázku a jednotky.
Zelená pole obsahují navržené hodnoty.
Žebrování je účinné řešení pro zvýšení teplosměnné plochy a tím i zvýšení přenosu tepla.
Pokud má obtékaný povrch žebrování, nastavte přepínač na "Ano".
Samotný tvar žebrování je definován v odstavci 4a. Přepnete se do něj tlačítkem ">>Definice [4a]."
Na základě rozměrů žebrování (odstavec 4a) je určena nová teplosměnná plocha At1, At2. Ta je použita pro návrhovou hodnotu A1 a A2 [4.37].
Žebrováním se sice zvýší plocha pro přestup tepla, ale zroveň se sníží účinnost přestupu tepla ηf1, ηf2. Touto účinností je opraven součinitel přestupu tepla hc1, hc2.
Pro zvětšení teplosměnné plochy jsou často pužívané svazky trubek. Pokud chcete řešit tuto úlohu, vyberte ze seznamu uspořádání trubek A nebo B (viz obrázek). Na následujících řádcích vyplňte parametry rozmístění trubek. Pro tuto úlohu je nutné aby médum 1 proudilo v trubce (01-06) a médium 2 obtékalo trubku (07-11).
Pokud je zvolena chybná kombinace typu proudění, je zobrazen nápis "Check".
Zadete vzdálenost mezi trubkami ve svislém směru ST a ve vodorovném směru SL podle obrázku.
Předvolená je dvojnásobná hodnota vnějšího průměru trubky.
Zadejte počet řad ve svislém směru m a vodorovném směru n podle obrázku.
V závislosti na uspořádání a počtu řad a sloupců je určen počet trubek ve svazku (zelená buňka).
Pokud se počet trubek u vaší úlohy liší, můžete zadat vlastní hodnotu. Tím ovlivníte návrh teplosměnné plochy.
Na řádku [4.24] zadáváte rychlost v2 rychlost proudění před vstupem do svazku trubek. Vložením trubek se zmenší průtočný průřez. Zvýší se tím rychlost proudění okolo trubek (v2max) pro méium 2.
V zeleném poli je navržená hodnota, která vychází ze zadaných rozměrů a rychlosti v2. Pokud je vaše konstrukce atypická, oškrtněte tlačítko a zadejte vlastní hodnotu.
V zeleném poli je navržená hodnota na základě dříve definovaných parametrů.
Pro médium 1 je to levá strana (pro plochu) a nebo vnitřní obvod x délka trubky. Pro médium 2 je to pravá strana (pro plochu) a nebo vnější obvod x délka trubky.
Pokud je zvoleno žebrování, nebo proudění přes svazek trubek (výměníky) je teplosměnná plocha příslušným způsobem změněna.
1. Svazek trubek ... A * počet trubek
2. Žebrování ... At (z odstavce Žebrování)
3. Svazek žebrovaných trubek ... At * počet trubek
Je kontrolován případ jednoduchého obtékání (bez žebrování), kdy teplosměnná plocha pro médium 1 by měla být menší a nebo rovna ploše pro médium 2. Pokud tomu tak není, jste upozorněni nápisem "Check".
Při používání kriteriálních rovnic, pro výpočet součinitele přestupu tepla hc, jsou pužívány bezrozměrné parametry (podobnostní čísla), které umožňují řešení podobných tvarů různých rozměrů a různých okolních podmínek. Podrobnější vysvětlení je v nápovědě nebo v oborné literatuře.
Ty nejdůležitější podobnostní čísla jsou zde uvedené.
Tlačítkem přesunete návrhovou (vypočítanou) hodnotu hc1, hc2 ze zelené buňky do vstupní buňky. Iterace proběhne 5x.
Nejdůležitěší podobnostní číslo je číslo Nusseltovo. Pro výpočet součinitele přestupu tepla hc pak platí následujíc vztahy:
Nu = hc * Dh / λ ===>
hc = Nu * λ / Dh
λ ... Tepelná vodivost materiálu stěny
Dh ... Charakteristický rozměr (D, Dh, a ..... na základě tvaru)
V zeleném poli je vypočítaný součinitel přestupu tepla hc1 a hc2. Výpočet vychází z parametrů proudícího média, teplot a typu proudění. Pokud jej chcete použít, stiskněte tlačítko Iterace "hc1<<, hc2<<".
Při změně hc1 a hc2 dojde zákonitě ke změně teplot a tím i ke změně parametrů proudícího média a k novému výpočtu hc. Proto je náhrada provedena 5x za sebou.
Menší tlačítka "hc1" a "hc2" pak nahrazují jen jeden koeficient.
Pro každé médium jsou uvedené dvě hodnoty
- tepelný tok vztažený na jednotku plochy (A1, A2)
- celkový tepelný tok plochou A1, A2
V této části výpočtu jsou řešené jednoduché případy sálání / ozáření.
- vyzařování do prostoru (například velká hala)
- vyzařování do prostoru (běžné atmosférické prostředí)
- ozáření plochy (například sluneční záření)
Pro většinu běžných situací jsou tyto případy dostatečné, pokud potřebujete řešit složitější úlohy z oblasti přenosu tepla zářením, použijte odstavec [7.0] a výsledek výpočtu použijte jako kladný / záporný tok záření dopadající na dannou plochu.
Na obrázku je naznačený tok energie (+) a (-) vzhledem k povrchu stěny 1 a 2.
Zvolte skupinu materiálů. Ukazatel v tabulce materiálů (následující řádek) bude nastaven na první materiál odpovídajícího typu.
Tlačítko "Search" se pokusí dohledat v tabulce materiálů odpovídající materiál první a poslední vrstvy stěny.
Vyberte materiál povrchu. V závorce za názvem je uvedena typická emisivita pro vybraný materiál. Pokud je uveden rozsah hodnot je jako návrhová hodnota (zelená) nabídnut jejich průměr.
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu emisivity povrchu stěny.
Určete, jestli dochází k vyzařování tepla do prostoru.
Zvolte odpovídající možnost (viz. obrázek)
A ... Není přestup tepla vyzařováním. Jde o uzavřenou plochu (Např. vnitřní stěna potrubí).
B ... Všeobecné vyzařování do prostoru (interiér i exteriér). Pro výpočet přestupu tepla zářením je použitá teplota média T1 resp. T2 vzhledem k teplotě stěny Ts1 resp. Ts2.
Pokud neznáte přesně podmínky, volte tuto možnost.
C, D, E ... Pro určení záření mezi stěnou a oblohou se stanovuje ekvivalentní teplota oblohy pro černé těleso Tsky [°K]. Tato teplota zohledňuje nerovnoměrnost teploty atmosféry a vyzařování v určitých vlnových délkách.
Výpočet tepelného toku qr' = ε * σ * (Tsky^4 - Ts^4)
Pro vztah mezi teplotou oblohy a místní teplotou vzduchu se používají přibližné vztahy:
C ... Tsky = Ta - 6°C
D ... Tsky = Ta - 12°C
E ... Tsky = 0.0552 * Ta^1.5 (platnost -30...+50°C)
kde Ta ... teplota okolního vzduchu [°K] (například: Ta = T2[°C] + 273.15)
V zeleném poli je navržená hodnota vyzařovací plochy. Pokud není použito žebrování nebo svazek trubek, je plocha Ar1, Ar2 shodná s teplosměnnou plochou A1, resp. A2. [4.37]
Pokud je zvoleno žebrování, nebo proudění přes svazek trubek je vyzařovací plocha příslušným způsobem změněna.
1. Svazek trubek ... A * počet krajních trubek / 2
2. Žebrování ... A + plocha krajních žeber
3. Svazek žebrovaných trubek ... případ 1 * případ 2
Pro každé médium jsou uvedené dvě hodnoty
- tepelný tok vztažený na jednotku plochy (A1, A2)
- celkový tepelný tok plochou A1, A2
Pokud potřebujete řešit jiný přenos tepla zářením než vyzařování do prostoru. Např: sluneční záření, údaje z odstavce [7.0], vlastní výpočet ….
Zadejte intenzitu záření dopadající na plochu. Přepínačem vpravo nastavíte:
- * 1: Výpočet použije přímo zadanou hodnotu a neuvažuje s emisivitou stěny ε. Předpokládá se, že emisivita je již zahrnuta do velikosti záření. Například výsledek výpočtu z odstavce [7.0].
- * ε: Výpočet vynásobí zadanou hodnotu výše zvoleným koeficientem emisivity stěny ε. Předpokládá se, že je známa úroveň záření. Například sluneční záření.
Sluneční záření
Jeho maximální hodnota na zemském povrchu se pohybuje okolo 1100 [W/m²] (350 [Btu/h/ft²]. Pro přesné hodnoty použijte odstavec [8.0]
Zadejte / Zvolte velikost ozářené plochy.
Po výběru první položky ze seznamu můžete zadat přímo velikost ozářené plochy Ai.
Další položky 1-5 (viz. obrázek) umožňují výpočet ozářené plochy Ai z teplosměnné plochy A1, A2 v závislosti na jejím tvaru.
Pro každou stranu stěny jsou uvedené dvě hodnoty
- průměrný tepelný tok vztažený na jednotku plochy A1, A2 (jelikož může být ozářena pouze část teplosměnné plochy, je vstupní hodnota "ir" vynásobena poměrem Ai/A).
- celkový tepelný tok plochou
Součet všech složek.
Součinitel přestupu tepla pro příslušnou stranu stěny. Zahrnuje proudění, vyzařování a ozáření.
Tepelný tok pro příslušnou stranu stěny. Zahrnuje proudění, vyzařování a ozáření.
Výpočet neřeší případnou změnu teploty proudícího média.
qcri' = qc' + qr' + qi' … měrný vztažený na jednotku vnitřní / vnější plochy
Qcri = Qc + Qr + Qi … celkový
Pro každé médium jsou uvedené dvě hodnoty
- tepelný tok vztažený na jednotku plochy
- celkový tepelný tok plochou A1, A2
Pro různé další výpočty je nutné znát celkový součinitel přestupu tepla stěnou U resp. tepelný odpor stěny R=1/U. Ve výpočtech se používají:
1) Hodnoty vztažené na vnitřní (1) nebo vnější (2) plochu. Jsou platné i pro válec a kouli.
2) Hodnoty vztažené na jednotku délky definovaného válce [4.5, 4.8].
3) Hodnoty vztažené na definovanou kouli [4.5, 4.8].
V literatuře, katalozích bývá často uváděn parametr "Tepelný odpor stěny". Jedná se pouze o tepelný odpor složené stěny definované v tabulce výše.
Pro rychlou orientaci je uveden i výpočet pro ohřátí / ochlazení pracovního média, pokud tomu odpovídá řešená úloha (kompletní výpočet, dlouhé potrubí, dlouhé obtékané plochy atd.).
Přepínačem mezi nadpisy volíte, jestli média proudí souběžně a nebo protiběžně.
Níže zadejte parametry proudícího média pro vnitřní (levou) stranu a pro vnější (pravou) stranu stěny pro teploty T1 a T2.
Při výpočtu navrhované průtočné plochy (zelená buňka) mohou nastat následující případy:
1) Tekutina proudí přesně definovaným průřezem (01-06). Hodnota v zeleném poli je přesná. Např. trubka s kruhovým průřezem Af = PI * (D/2)^2
2) Tekutina obtéká potrubí (07-11). Je navržena hodnota, která se rovná kolmému řezu potrubí (vnější rozměr). Např. kruhová trubka Af = D * L
3) Tekutina proudí svazkem trubek. Af = m * ST * L
4) Volné proudění (13-19). Průtočná plocha se rovná obtékané ploše
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
Ze zadané rychlosti proudění v1 (v2) [4.24], průtočné plochy Af a hustoty Rho je spočítán průtok.
V seznamu napravo můžete vybrat jednotky, které se zobrazují.
Ze zadané teplosměnné plochy A [4.37], průtočné plochy Af hustoty Rho, měrné tepelné kapacity Cp', průtoku m' a vypočteného součinitele přestupu tepla U je vypočítána teplota na výstupu Tout1 a Tout2.
Tepelný tok je počítán z rozdílu teplot média na vstupu a výstupu a z vlastností pracovního média.
Tepelný tok se tak liší od údajů Qcri [4.62], kde není uvažována změna teploty média.
Pro každé médium jsou uvedené dvě hodnoty
- průměrný tepelný tok vztažený na jednotku plochy
- celkový tepelný tok plochou A1, A2
Řešení přestupu tepla stěnou vyžaduje zadání a volbu desítek parametrů. Proto je možné řešení pojmenovat a opatřit komentářem a uložit si ho do seznamu pro další, budoucí použití, nebo pro načtení parametrů v jiných odstavcích tohoto výpočtu.
Aktuální stav všech parametrů - řešení uložíte tlačítkem "Uložit řešení".
Řešení se ukládají do listu "Stěny". Jeden řádek obsahuje jedno uložené řešení.
Při stisknutí tlačítka "Uložit řešení" je prohledán seznam a pokud existuje záznam se stejným jménem je přepsán aktuálním stavem. Pokud neexistuje jméno v seznamu řešení, je nalezen poslední vyplněný řádek na listu "Stěny" a aktuální řešení je zapsané na řádek následující.
List "Stěny" je volně přístupný a je možné jej normálně editovat prostředky excelu (například vymazání nepotřebných řešení - řádků).
Zjištění jedné hodnoty z uloženého řešení.
Pokud potřebujete zjistit konkrétní hodnotu a použít ji ve vlastním vzorci, je připravená funkce GetWallProp, která to umožňuje.
Syntaxe:
GetWallProp(ID;value_name)
ID ... Číslo řádku na listu "Stěny", který obsahuje uložené řešení
value_name ... Jméno hodnoty, kterou chcete zjistit.
Zadejte název řešení přestupu tepla stěnou.
Pod tímto názvem bude řešení uložené v seznamu uložených řešení.
Automaticky generovaný text, který se přidává do popisu a obsahuje základní info ve kterém jsou:
T1(),T2() … Teploty, (médium)
|mm| … Tloušťka stěny
U1 … Součinitel přestupu tepla
q1,q2 … Celkový měrný tepelný tok
Zadejte popis. Umožní vám to lepší orientaci při následném prohlížení již uložených řešení.
Po výběru řešení z výběrového seznamu níže stiskněte tlačítko "Načíst řešení".
Tlačítky vpravo se pohybujete v seznamu uložených řešení.
Datum uložení řešení je ve formátu "yyyymmdd - hh:mm:ss".
Výběrový seznam obsahuje řešení přestupu tepla stěnou, které jsou uložené na listu "Stěny".
Základní info o vybraném řešení přestupu tepla stěnou.
Popis vybraného řešení přestupu tepla stěnou.
Tento odstavec je přímo napojený na odstavec předchozí a řeší žebrování obtékané plochy. Používá se pro zvýšení teplosměnné plochy a tím i zvýšení přenosu tepla.
Pro použití musí být v předchozím odstavci zapnuté použití žebrování [4.29].
Na základě volby typu proudění v předchozím odstavci [4.23] je přiřazen odpovídající typ žebrování 1-4 dle obrázku.
Z předchozího odstavce [4.0] jsou pro výpočet žebrování použité hodnoty λ, hc, T a Ts.
Pro tepelnou vodivost materiálu λ je použitá hodnota první a poslední vrstvy složené stěny.
V závislosti na volbě typu proudění [4.23] a zadaných rozměrů je dopočítána šířka žebrovaného pole "a" pro typ žebrování:
1) a = délka plochy
2) a = délka trubky
3) a = vnitřní obvod trubky
4) a = vnější obvod trubky
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu šířky pole.
Vyberte tvar žebra podle obrázku.
Na základě rozměrů žebrované plochy a typu proudění jsou přednastavené rozměry žebra (zelené buňky). Po odškrtnutí tlačítka můžete zadat vlastní rozměry.
V zelené buňce je navržený maximální počet žeber, které je možné použít vzhedem k šířce pole a rozměrům žebra. Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
Například pokud je žebrováním opatřena jen část plochy / trubky).
- Af ... Plocha jednoho žebra (pouze žebro).
- At ... Kompletní teplosměnná plocha (plocha žebra x počet žeber + zbývající plocha základního profilu).
Hodnota kompletní teplosměnné plochy žebrování At je použitá jako doporučená hodnota na řádku [4.34].
Parametr x slouží k vyhledání účinnosti žebrování v příslušných grafech (provede výpočet).
Celková účinnost zahrnuje poměr plochy žeber k celkové žebrované ploše a je použit při výpočtu tepelného toku qc', Qc [4.43].
V odstavci je řešena změna teploty proudící látky v potrubí a čas ochlazení pro zadaný pokles teploty v potrubích, nádobách a zásobnících.
Vyberte látku proudící v potrubí.
Pokud není látka v seznamu zadejte na řádku [5.3] hodnotu Cp.
Zadejte definiční teplotu. Z teploty bude pro zvolenou látku vypočtena hodnota Cp na řádku [5.3].
Přednastavená hodnota (zelené pole) je teplota T1 z odstavce [4.0].
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu Cp.
Výpočet umožňuje zjistit teplotu proudící látky v potrubí v zadané vzdálenosti od vstupu.
Předpokládá se, že teplota okolí je konstantní.
Není nijak kontrolována teplota fázové změny látky.
V zelených polích jsou návrhové hodnoty přejaté z odstavce [4.0].
Po odškrtnutí tlačítka můžete zadat vlastní hodnoty.
Je nutné zadat součinitel přestupu tepla vztažený na jednotku délky potrubí.
Hodnota Pw udává ztrátový výkon (-), nebo příkon (+).
Výpočet umožňuje zjistit čas ochlazení látky v zásobníku (nádobě, potrubí) z teploty T1s na teplotu T1e.
Předpokládá se, že teplota okolí je konstantní.
Není nijak kontrolována teplota fázové změny látky.
V zelených polích jsou návrhové hodnoty přejaté z odstavce [4.0].
Po odškrtnutí tlačítka můžete zadat vlastní hodnoty.
Zadejte koncovou teplotu, které chcete dosáhnout. Výsledkem výpočtu bude čas nutný pro dosažení teploty T1e.
Zadejte hmotnost látky v zásobníku (nádobě, potrubí).
Zadejte součinitel přestupu tepla vztažený na jednotku vnitřní plochy zásobníku.
Hodnota E udává energetickou ztrátu (-), nebo energetický zisk (+).
V odstavci jsou řešené základní typy výměníků tepla (souproud, protiproud, souproud+protiproud, složený souproud+protiproud, křížový průtok).
Vyberte odpovídající typ výměníku, který chcete řešit. Při výběru se řiďte obrázky A-G.
Ve výpočtu jsou řešené základní úlohy. Nicméně je možné jej použít i pro řešení složitějších typů výměníků tepla, pokud znáte jejich korekční součinitel [6.17].
Výpočet výměníku závisí na správně určeném koeficientu přestupu tepla U. Ten přesně určíte v odstavci [4.0]. Můžete načíst aktuální hodnoty z odstavce [4.0] a nebo vybrat uložené řešení stěny ze seznamu stěn a načíst jeho hodnoty.
Pokud znáte koeficientu přestupu tepla, můžete ho zadat přímo na řádku [6.21]. V nápovědě jsou uvedené i charakteristické hodnoty pro častá řešení.
Po stisknutí tlačítka vpravo se načte:
- koeficient přestupu tepla
- výběr pracovní látky
- teploty T1,T2
- hmotnostní tok
Vyberte pracovní látky použité ve výměníku.
Pokud není látka v seznamu zadejte na řádku [6.7] hodnotu Cp1 a Cp2.
Zadejte definiční teplotu. Z teploty bude pro zvolenou látku vypočtena hodnota Cp na řádku [6.7].
Přednastavená hodnota (zelené pole) je průměr teplot T1in a T1out (resp. T2in a T2out pro T2def).
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu Cp.
Výpočet teplotního toku Q pro zadané parametry toku pracovních látek a jejich teplot.
Následující řádky udávají parametry pracovní látky 1 a 2. (hmotnostní tok, vstupní teplota, výstupní teplota).
V zeleném poli je návrhová hodnota, která je nutná pro dosažení rovnováhy teplotního toku (platnost Q1 = - Q2).
Vedle zeleného pole je tlačítko "◄", které přesune návrhovou hodnotu do hodnoty vstupní.
Při každé změně libovolné vstupní hodnoty jsou v zelených buňkách dopočítané odpovídající hodnoty pro dosažení rovnováhy teplotního toku (Q1 = - Q2).
Například nesmyslné řešení typu:
- pracovní látka 1 s teplotou T1<T2 má ohřát pracovní látku 2
- pracovní látka 1 nedokáže dodat/odebrat množství tepla které je
odebrané/dodané pracovní látkou 2
Tepelný tok mezi látkou 1 a 2. Tepelný tok musí být shodný (+) (-).
Na základě teplotního toku je možné následně určit velikost teplosměnné plochy.
Po definici hmotnostního toku, teplot a tím i teplelného toku je stanoven střední logaritmický teplotní rozdíl ΔT'.
Ten je nutný k výpočtu potřebné teplosměnné plochy.
Koeficienty R a P jsou nutné pro určení ɛ [6.17].
R … Poměr tepelné kapacity R / The heat capacity ratio R
R = (T1Kin - T1Kout) / (T2Kout - T2Kin)
P ... Tepelná účinnost P / Temperature Effectiveness P
P = (T2Kout - T2Kin) / (T1Kin - T2Kin)
Odpovídající grafy pro ɛ pro mnoho typů výměníků jsou dostupné v uvedené literatuře.
Pro složitější typy výměníku se pro určení středního logaritmického rozdílu používá korekční součinitel ɛ. Pro výměníky typu C-G je určen aproximací z tabulek (jsou na listu "Tabulky").
Pro výměníky, které nejsou definované v tomto programu je možné určit součinitel ɛ z grafů R-P-ɛ, které je možné nalézt v odborné literatuře (např. Heat Exchanger Design Handbook a další). Grafy jsou většinou uváděné pro mnoho typů výměníků.
Velikost součinitele se pohybuje v rozmezí 0.5-1.0
Výměník je možné řešit jako deskový a nebo jako trubkový. Většinou rozhoduje konstrukce výměníku o tom, který způsob je výhodnější. Vyberte typ ze seznamu.
- Deskový výměník
Součinitel prostupu tepla U je definován na jednotku plochy.
Pro požadovaný tepelný tok je vypočtena teplosměnná plocha.
- Trubkový výměník
Součinitel prostupu tepla U je definován na jednotku délky trubky.
Pro požadovaný tepelný tok je vypočtena délka trubky.
Pokud načtete definici stěny z odstavce [4.0] nebo ze seznamu, je v zeleném poli je odpovídající hodnota. Pokud chcete zadat vlastní hodnotu odškrtněte tlačítko.
Orientační rozsah hodnot Upl pro různé kombinace látek ve výměnících tepla.
Podle volby typu [6.19] je vypočtena nutná plocha, nebo délka trubky.
Výpočtem určíte výstupní teplotu T1Out a T2Out v závislosti na velikosti teplosměnné plochy nebo délce trubky.
Zadejt velikost teplosměnné plochy, resp. délku trubky.
Pro zadané parametry:
- m1', m2' … [6.9]
- T1in, T2in … [6.10]
- Upl nebo Ucyl … [6.21]
- A nebo L … [6.24]
Zjistíte teplotu na výstupu T1Out, T2Out
Po stisknutí tlačítka "▲T1out, ▲T2out" jsou vypočtené hodnoty přenesené na řádek [6.11].
Jednoduchý přepočet plochy na délku trubky a naopak. Podle toho, jaký je zvolen typ výměníku [6.19] je proveden přepočet plochy [6.22] na délku trubky a nebo délky trubky [6.22] na plochu.
- Ze seznamu vyberte profil trubky (A-E)
- Zadejte plochu nebo délku trubky (předvolená hodnota z [6.22])
- Zadejte rozměry profilu podle obrázku (předvolené hodnoty jsou podle načtené stěny [6.3, 6.4])
Při provozu může dojít k pokrytí plochy usazeninami, nebo k oxidaci. To zvyšuje odpor a snižuje výkon výměníku. Zvýšení odporu se vyjadřuje koeficientem znečištění Rf = 1/Ud - 1/Uc [m²K/W], [h.ft²F/Btu]
Koeficient se zjišťuje experimentálně nebo je možné použít tabulku doporučených hodnot [6.35] pro různé média.
Zadejte plošný součinitel přestupu tepla pro čistou plochu.
Zadejte koeficient znečištění Rf. Pokud neznáte hodnotu (například z měření), můžete se řídit hodnotami z tabulky.
Pokud jsou znečištěné obě plochy výměníku (vnitřní i vnější) zadejte součet Rf.
Součinitel přestupu tepla pro znečištěnou plochu a procentuální rozdíl mezi Uc a Ud. Snižte hodnotu Upl (Ucyl) [6.21] o příslušný procentní rozdíl.
Tlačítkem "▲U" přímo snížíte hodnotu Upl (Ucyl) [6.21].
Čárkovaně je zobrazena průměrná teplota (Tin+Tout)/2
Modrá … médium 1
Zelená … médium 2
Stisknutím tlačítka "<---->" zaměníte médium 1 za médium 2 a naopak.
V odstavci jsou řešené základní úlohy přestupu tepla zářením.
A…Sálání do prostoru (plocha, válec, koule, obecný tvar)
Pro vyzařování do volného prostoru v pozemské atmosféře je často používán vztah Tsky=Teplota vzduchu - 6°C nebo Tsky=Teplota vzduchu - 12°C (Odhad zahrnující vliv vyzařování v atmosféře). Pro kosmický prostor je možné použít Tsky=-270°C.
B…Sálání mezi dvěma rovnoběžnými povrchy (plocha, válec, koule)
C…Sálání mezi dvěma rovnoběžnými povrchy s jednou stínící fólií x (plocha, válec, koule)
D…Sálání mezi dvěma rovnoběžnými povrchy s dvěma stínícími fóliemi x,y (plocha, válec, koule)
Předpoklady a zjednodušení:
1) Prostředí mezi povrchy musí být průteplivé. Není řešen typ prostředí (vakum, typ plynu...)
2) Pro výpočet je uvažována fólie s "nulovou" tloušťkou a "nekonečnou" tepelnou vodivostí.
3) V případě rovinné plochy musí být vzdálenost ploch řádově menší než rozměry ploch.
4) V případě válcové plochy je předpoklad, že délka válce L je řádově větší než průměr D
5) Je možné zvolit rozdílnou emisivitu stínící fólie pro každou stranu fólie.
6) V případě nekoncentrických ploch (4), jsou platné jen hodnoty celkového tepelného toku Q12.
Podle vybrané úlohy jsou vypnuté vstupní sekce - šedivá políčka
Zvolte skupinu materiálů. Ukazatel v tabulce materiálů (následující řádek) bude nastaven na první materiál odpovídajícího typu.
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu v rozmezí [0…1].
Zadejte teplotu stěny T1, T2.
V případě, že je řešeno vyzařování do prostoru, zadejte teplotu prostoru Tsky.
Vyberte ze seznamu typ plochy
1. Rovinná plocha: Zadaná plocha (1) je promítnutá do plochy 2, X, Y.
2. Válcová plocha: Délka válce z (1) je promítnutá do 2, X, Y. Průměry válce je možné volit libovolně v 1,2,X,Y za podmínky že D1
3. Kulová plocha: Průměry je možné volit libovolně v 1,2,X,Y za podmínky že D1
4. Obecná plocha: Je určené pro výpočet tepelného toku mezi plochou 1, která je plně uzavřena v ploše 2. Velikost plochy je možné volit libovolně v 1,2,X,Y za podmínky že A1
U obecné plochy se předpokládá, že plochy nejsou nijak uzavřené do sebe.
Na základě volby a údajů na předchozím řádku je nabídnuta vypočtená hodnota plochy A. Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
Parametry stínících fólií jsou obdobné jako u stěny, s tím že je uvažována fólie s "nulovou" tloušťkou a "nekonečnou" tepelnou vodivostí a je nutné přímo zadat emisivitu obou stran.
Zadejte emisivitu stínící fólie pro levou a pravou stranu. Vodítkem mohou být hodnoty ze seznamu výše.
Je závislý na volbě [7.07]
Pro válec a kouli je možné volit průměr. Ostatní hodnoty jsou definované povrchem 1.
Po odškrtnutí tlačítka zadejte vlastní hodnotu.
Podmínka: A1<=Ax<=Ay<=A2, na nesplnění podmínky upozorňuje červený text.
Jsou uvedené dvě hodnoty.
1) Měrný tepelný tok na jednotku plochy. Pokud se plocha A1<>A2 (válec, koule, obecná plocha) jsou hodnoty rozdílné pro každou plochu.
2) Celkový tepelný tok pro zadanou plochu.
V odstavci je řešené základní teplotní zatížení slunečním zářením (doba, čas, poloha, orientace plochy …).
Řada strojírenských (stavebních) konstrukcí je vystavena slunečnímu záření. Výpočet slouží pro určení slunečního teplotního toku na plochu pro zadané podmínky (orientace plochy, datum, hodina, nadmořská výška, znečištění) a k určení celkového denního příkonu.
Tlačítkem "▼▼" nastavíte aktuální datum a čas.
Zadejte měsíc a den ve kterém chcete zjistit hodnotu slunečního toku.
Tlačítky -/+ můžete měnit vstupní hodnoty a sledovat na grafech změny.
Číslo mezi tlačítkem - a + udává krok změny.
Neplatný den je zvýrazněn červeně.
Zadejte hodinu a zeměpisnou šířku, pro které chcete zjistit hodnotu slunečního toku.
Tlačítky -/+ můžete měnit vstupní hodnoty a sledovat na grafech změny.
Číslo mezi tlačítkem - a + udává krok změny.
Zeměpisná šířka měst.
Zadejte sklon plochy vůči vodorovné rovině (0=vodorovná, 90=kolmá)
Zadejte azimut normály plochy (0=S, 90=W, -90=E, 180=N).
Příklad orientace SW=45
Tlačítky -/+ můžete měnit vstupní hodnoty a sledovat na grafech změny.
Číslo mezi tlačítkem - a + udává krok změny.
Čas východu a západu slunce (pro střed slunce) berte jako orientační. Neřeší zemepisnou délku, letní/zimní čas atd.
Délka slunečního svitu pro zadané vstupní parametry.
Pokud kombinace datumu a zeměpisné šířky vede k:
Polární den … východ/západ slunce = 0/24, Délka slunečního svitu = 24
Polární noc … východ/západ slunce = 12/12, Délka slunečního svitu = 0
Úhel elevace slunce φ je úhel mezi sluncem a (ideálním) horizontem pro zadané parametry MM,DD,HH.
Sluneční deklinace δ je úhel slunce od roviny rovníku pro zadaný datum MM,DD.
(φ=0) ... Východ a západ slunce: Okamžik, kdy geometrický střed slunce přechází přes horizont
(φ=-6)... Občanský rozbřesk / soumrak začíná resp. končí okamžikem, kdy se střed slunečního kotouče nachází 6° pod horizontem. Při občanském rozbřesku / soumrak lze venku bez umělého osvětlení vykonávat běžné činnosti jako např. číst noviny nebo hrát míčové hry.
(φ=-6...-12) ... Nautický rozbřesk / soumrak: Při nautickém rozbřesku / soumraku se střed slunečního kotouče nachází mezi 6° a 12° pod horizontem. Jsou vidět první hvězdy a zároveň je horizont zřetelně rozeznatelný.
(φ=-18) ... Astronomický rozbřesk / soumrak: Astronomický rozbřesk / soumrak přináší první a poslední sluneční paprsky dne. Obloha je velmi tmavá, je vidět výrazně hvězdy. Pokud slunce dále klesne pod horizont více než 18°, nastává astronomická noc. Pokud slunce okolo letního slunovratu neklesá víc než 18° pod horizont, večerní astronomický soumrak splývá s raním svítáním a astronomická noc tak nenastává.
Sluneční zářivý tok vně atmosféry se mění v průběhu roku o +-3.3% (vzdálenost země-slunce). Hodnota ve střední vzdálenosti Země-Slunce je 1367W/m².
Další nastavení zpřesňují zářivý tok vzhledem k atmosféře, znečištení atd.
Nadmořská výška definuje tloušťku a hustotu vzduchové vrstvy, která ovlivňuje hustotu tepelného toku.
Volbou z výběrového seznamu přenesete hodnotu do vstupní buňky.
Zahrnuje vlivy znečištění atmosféry pro různé oblasti a pro roční období.
Z=1 ... Průchod zcela čistým vzduchem
Z=2 … Horské oblasti
Z=3 … Venkov
Z=4 … Město
Z=>5 … Průmyslová oblast
Pro zimní období - 20%
Pro letní období + 10%
Volbou z výběrového seznamu přenesete hodnotu do vstupní buňky.
γs … Azimut slunce je úhel mezi jihem (S) a polohou slunce pro zadané vstupní hodnoty.
Θ … Úhel dopadu slunečního záření je úhel mezi spojnicí středu Slunce a normálou plochy "n" pro zadané vstupní hodnoty.
QbT … reálná hodnota záření, které dopadá na definovanou nakoněnou plochu (sklon a orientace).
Qbn … záření, které dopadá na kolmou plochu (vůči poloze Slunce) po průchodu atmosférou pro zadané vstupní údaje (Datum, místo, znečištění…).
QdT ... difúzní sluneční ozáření na danou plochu.
Qdt = ((1 + cos(beta)) / 2) * Qd
Qd ... Je použitý zjednodušený odhad, ve kterém se uvažuje s tím, že na vodorovnou plochu dopadá zhruba jedna třetina slunečního záření, které se "ztratí" v atmosféře.
Qd = 0.33 * (Qon - Qbn)
Albedo - Poměr mezi odraženou a dopadlou hustotou slunečního zářivého toku. Pro výpočty je možné použít Rhog= 0.2
Hodnoty:
0.10 až 0.15 ... běžná vegetace
0.90 ... sníh
0.35 - 0.45 ... zemský povrch: souš
0.05 - 0.10 ... zemský povrch: moře
0.30 (průměr) ... Albedo Země (planety)
QrT … odražené sluneční ozáření na danou plochu.
Qrt = Rhog * ((1 - cos(beta)) / 2) * (Qb + Qg)
Zadejte velikost ozařované plochy.
Sluneční ozáření obecně orientované plochy pro zadaný čas a zadanou polohu. Součet všech složek (přímé, difuzní, odrazivé)
QT … Celková energie na zadanou plochu
QT' … Energie na jednotku plochy
Hodnota udává, kolik slunečního záření je převedeno na využitelnou energii. Obecně je možné volit z následujících hodnot. Přesné hodnoty naleznete u výrobce či dodavatele.
Přímá přeměna na elektřinu:
Fotovoltalické panely - Účinnost moderních panelů (rok 2025) se pohybuje v rozmezí 18-24% (pro 25C). Je závislá na teplotě, léto až -20%, zima až +10%.
Ohřev vody, vytápění:
Účinnost je závislá na teplotě média, které je ohřívané, na konstrukci atd. Je možné použít následující orientační hodnoty. V závorce je teplota pracovního média.
Deskové kolektory - 95% (0C), 70% (40C), 40% (80C), 20% (100C)
Vakuové trubkové kolektory: 70% (0C), 55% (40C), 40% (80C), 30% (120C), 20% (140C)
Sluneční ozáření vynásobené účinností.
(měrné na jednotku plochy, celkové na plochu)
Výkon plochy pro zadaný den za předpokladu nulové oblačnosti (měrný na jednotku plochy, celkový na plochu).
V závislosti na zadané zeměpisné šířce je zobrazen čas východu a západu slunce pro den 1-365.
Declination … Úhel slunce od roviny rovníku (δ) pro den (1-365).
Zobrazení průběhu hodnot pro den 1-365:
- Sluneční konstanta (Qon) [W/m²].
- Výška slunce nad obzorem (φ) pro zadanou hodinu.
- Zářivý výkon (Qbn) [W/m²] na plochu kolmou na Slunce pro zadanou hodinu .
Zobrazení průběhu hodnot pro hodinu (0-24):
- Výška slunce nad obzorem
- Celková hodnota slunečního ozáření (QT=QbT+QdT+QrT)
- Jednotlivé složky QbT, QdT, QrT
Hodnoty jsou v [W/m²]
Excel obsahuje doplňek "Řešitel" ("Solver"), což je vestavěný nástroj pro řešení lineárního i nelineárního programování. Pokud je nutné řešit složitější úlohy přestupu tepla, je možné si zde přehledně připravit data pro tento doplněk. Je tak možné navrhnout model a řešit například úlohy, kde dochází k současnému přestupu tepla v několika různých stěnách. Tento odstavec je umístěn na samostatném listu "Řešitel" (druhý list), list není zamknutý.
Postup:
1. Připravte si tabulku řešených přestupů tepla pro jednotlivé stěny [9.6].
2. Definujte pomocí vztahů excelu matematický model. [9.5, 9.6, 9.7].
3. Použijte doplněk "Řešitel" ("Solver") pro řešení modelu.
V odstavci [4.0] je řešen přestup tepla pro stěnu. Do tabulky níže můžete přenést aktuální hodnoty a nebo hodnoty z tabulky uložených řešení.
Vyberte řešení stěny ze seznamu. Po stisknutí tlačítka "Přidat/Nahradit" je vybrané řešení přidané buď na řádek, ve kterém je aktivní buňka a nebo na první řádek bez popisu v definiční tabulce níže. Pokud již řádek obsahuje nějaké hodnoty, jsou přepsány. Tlačítkem "Vymazat vše" odstraníte všechny řádky.
Ve výběrovém seznamu vyberte, která hodnota bude přenesena do odpovídajícího sloupce. Pokud vyberete první položku "Nevyplnit", zůstane ve sloupci původní hodnota.
Značení je stejné jako v odstavci [4.0].
Dva sloupce, které můžete použít pro různé mezivýpočty.
Do tabulky si připravte hodnoty pro všechny stěny, které použijete v matematickém modelu pro "Řešič" ("Solver").
Použití doplňku "Řešitel" ("Solver") vyžaduje definici matematického modelu, který popisuje řešenou úlohu.
Pro zjednodušení a přehlednost jsou připravené tři oblasti (vstupní hodnoty, výstupní hodnoty a podmínky). Zde si můžete pomocí vzorců excelu odpovídající matematický model přehledně definovat.
Samozřejmě, že rozložení a definici matematického modelu si můžete připravit zcela podle svých požadavků. Není třeba se řídit navrženým uspořádáním.
Spuštění doplňku "Řešitel" ("Solver") naleznete v menu (Ribbon) excelu "Data".
Jednoduchý, názorný příklad úlohy, definice modelu a spuštění "Řešitele" ("Solver") ve třech krocích. Příklad řeší velikost zdroje tepla QH pro získání teploty T2 v místnosti ze čtyřech různých stěn a okolní teplotou T2.
Níže jsou řešené následující příklady:
Příklad 01 - Periodická tabulka prvků - parametry směsi plynů (m, r, κ) - vzduch
Příklad 02 - Periodická tabulka prvků - parametry plynu (m, r, κ) - sirovodík
Příklad 03 - Ideální plyn - Plnění tlakové láhve
Příklad 04 - Ideální plyn - změna objemu přivedením energie (isobarická změna)
Příklad 05 - Ideální plyn - Smíšení plynů s různými parametry (m, p, V, T)
Příklad 06 - Ideální plyn - Polytropické stlačení (kompresor)
Příklad 07 - Ideální plyn - Oběh pístového kompresoru
Příklad 08 - Komplexní přenos tepla válcovou trubkou (sálání, konvekce, vedení
tepla)
Příklad 09 - Uložení a načtení řešení přestupu tepla stěnou, zjištění hodnot
Příklad 10 - Částečné řešení přestupu tepla (sálání nebo konvekce nebo vedení
tepla)
Příklad 11 - Přestup tepla stěnou, která má z jedne strany vakuum (Termoska)
Příklad 12 - Přestup tepla žebrovanou stěnou, která je kontaktně ohřívána z
jedné strany (TEG el.generátor)
Příklad 13 - Přestup tepla - svazek kruhových trubek (10 x 8)
Příklad 14 - Přestup tepla - svazek kruhových žebrovaných trubek (7 x 6)
Příklad 15 - Změna teploty a čas ochlazení kapaliny v nádobě (Termoska)
Příklad 16 - Výměník tepla - Protiproud (Voda / Olej)
Příklad 17 - Výměník tepla - Jednoduchý - křížový průtok s oběma nemíchanými
kapalinami
Příklad 18 - Přestup tepla zářením mezi dvěma rovnoběžnými plochami
Příklad 19 - Přestup tepla zářením mezi dvěma rovnoběžnými plochami s jednou
stínící fólií
Příklad 20 - Sluneční záření - hodnoty pro orientovanou plochu, zeměpisnou
polohu, čas a prostředí
Příklad 21 - Tepelná bilance budovy: Řešič ("Solver"), přestup tepla v objektu,
topení, teploty místností
Výpočet parametrů směsy plynů - vzduch (Molární hmotnost ... M, Měrná plynová konstanta ... r, Poissonova konstanta ... κ).
Vzduch: je směs N2+O2+Ar+CO2
Hmotnostní podíl: (N2...75.518, O2...23.1354, Ar...1.288, CO2...0.059)
Zadejte směs plynů, tlačítkem rozdělíte do tabulky.
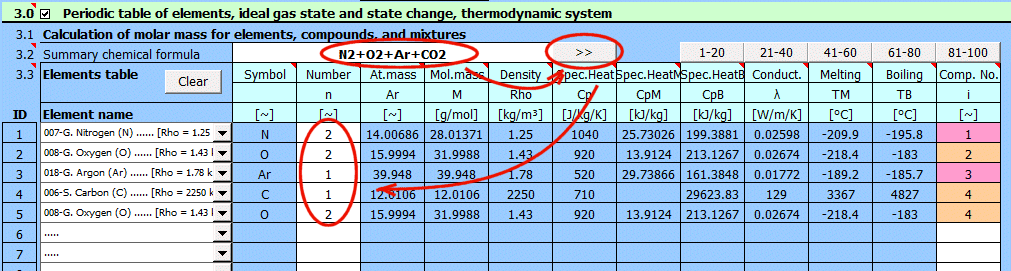
Zadejte hmotnostní podíl jednotlivých složek a zjistíte potřebné hodnoty směsi plynů.

Tlačítkem "▼M,κ▼" přenesete hodnoty do výpočtu parametrů ideálního plynu.
Výpočet parametrů plynu - sirovodík (Molární hmotnost ... M, Měrná plynová konstanta ... r, Poissonova konstanta ... κ).
Vzorec: H2S
Zadejte vzorec.

Hmotnostní podíl je 100%.
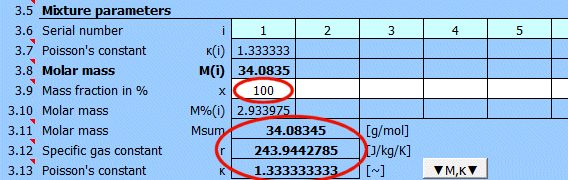
Tlačítkem "▼M,κ▼" přenesete hodnoty do výpočtu parametrů ideálního plynu.
Jak se změní hmotnost 15L tlakové láhve pokud ji naplníme vzduchem o tlaku 20MPa, při teplotě 20C?
Vyberte jako pracovní látku vzduch a nastavte teplotu.

Zadejte vlastnosti pro atmosférický tlak 101kPa.
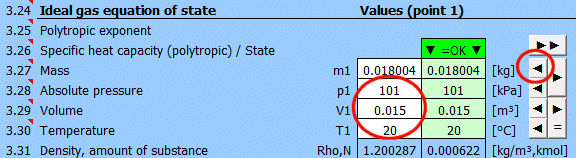
Zadejte nový tlak 20MPa = 20000kPa a stiskněte tlačítko.
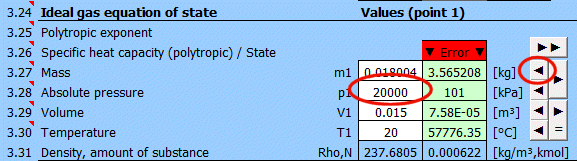
Výsledkem je nová hmotnost obsahu láhve.
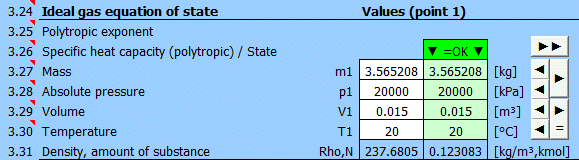
Hmotnost se zvýší o 3.565 - 0.0182 = 3.5468kg.
Ve válci pod pístem je vzduch. Do válce je přivedeno 300kJ tepla. Určete změnu T a V, p1=p2.
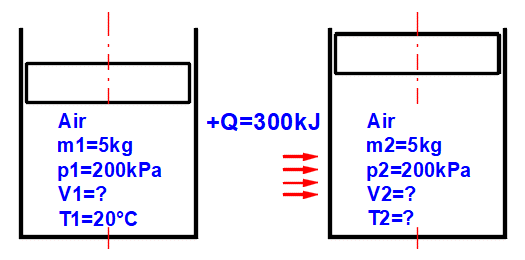
Vyberte jako pracovní látku vzduch a nastavte teplotu.

1. Zadejte hodnoty m1, p1, T1
2. Stiskněte tlačítko "◄" pro vyplnění V1
3. Tlačítkem "►►" rozkopírujte hodnoty do ostatních bodů
4. Postupně měňte teplotu T2, dokud není hodnota Q=300kJ
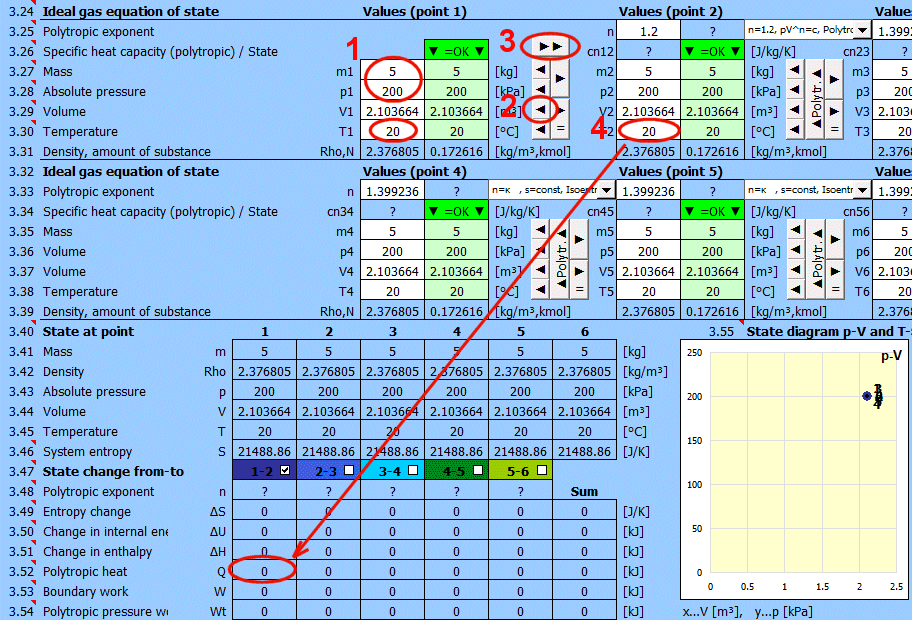
Stiskněte tlačítko "◄" pro vyplnění V2.
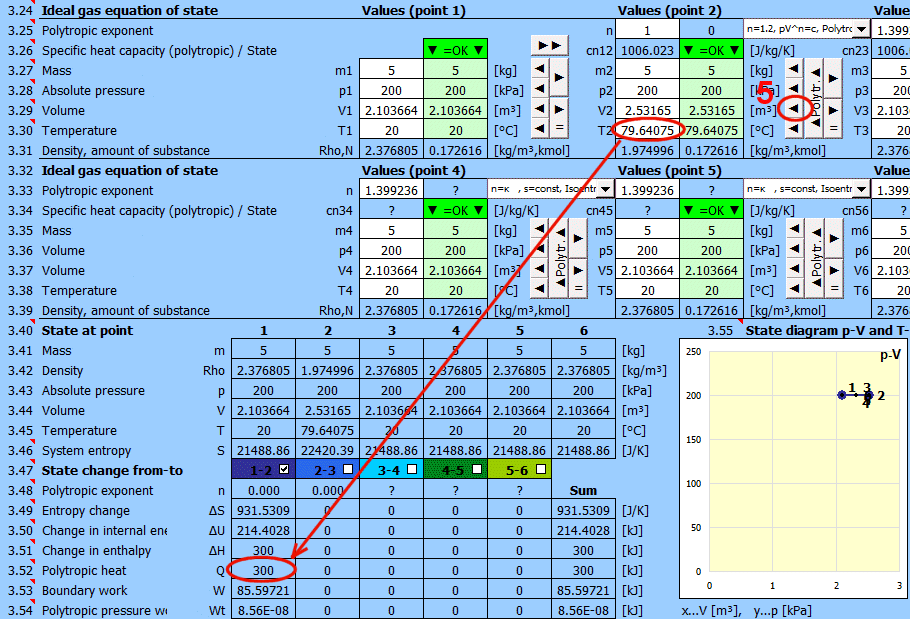
Dvě spojené nádoby, které obsahují vzduch o různých parametrech. Po otevření spojovacího ventilu dojde ke smíšení plynů a poté k ochlazení na konečnou teplotu 25C.
Určete koncový tlak, teplotu, změnu energie...
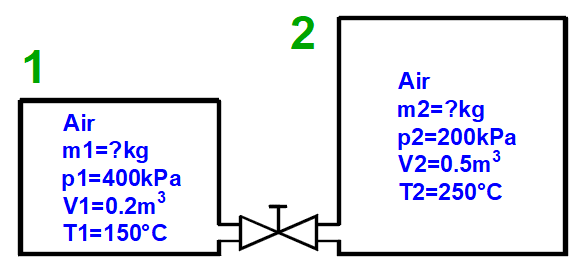
Vyberte jako pracovní látku vzduch a nastavte teplotu odhadem na 100C.

1. Nastavte parametry nádoby 1
2. Vyplňte odpovídající hmotnost plynu m1
3. Nastavte parametry nádoby 2
4. Vyplňte odpovídající hmotnost plynu m2
5. Stiskněte tlačítko pro výpočet parametrů výsledné směsi.
V bodě 3 jsou spočítané parametry plynu, které nastanou smísením 1+2
6. Přesuňte výsledné parametry do bodu 4
7. Zadejte konečnou teplotu celé soustavy T4
8. Vyplňte odpovídající tlak plynu p4
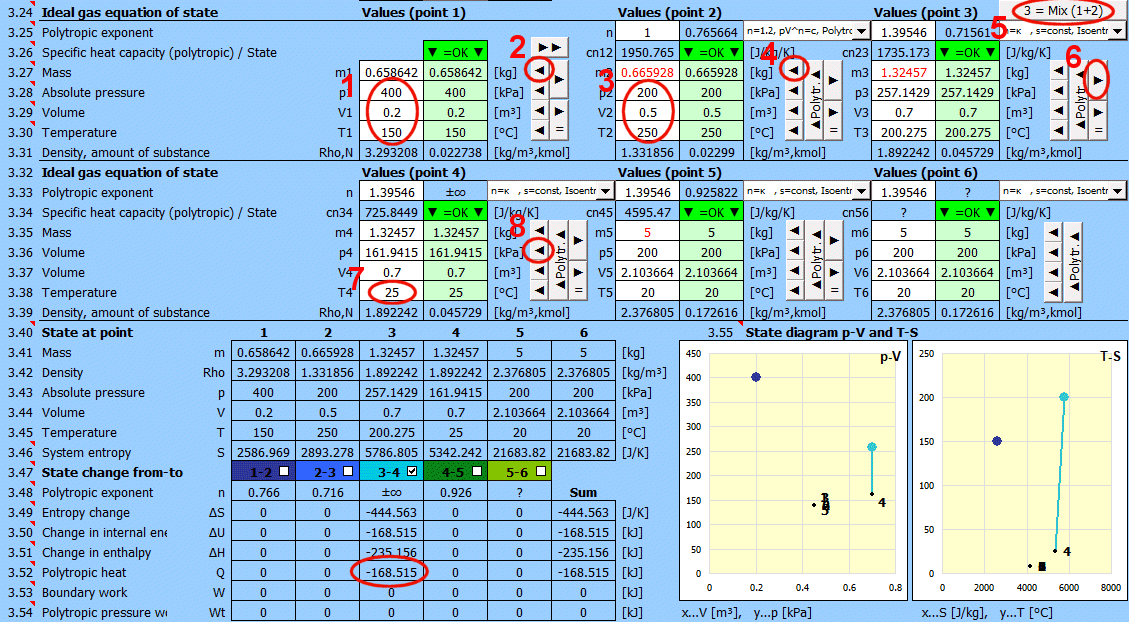
The change in energy (heat removed Q) is the change between 3-4. To cool the mixture (from point 3), 168kJ of heat must be removed.
Při polytropickém ději se obecně mění všechny stavové veličiny (p,V,T). Pro
polytropický děj v ideálním plynu platí rovnice p*V^n = const.
Pro pístový kompresor: n=1.2–1.3 (Proces s částečným odvodem tepla, typická
hodnota pro pomalé kompresory s chlazením).
Počáteční parametry vzduchu: m1=?, p1=150 kPa, V1=260 m³, T1=27 °C.
Je stlačen pístovým kompresorem s polytropickým exponentem n=1.2
Na koncové hodnoty: m2=m1, p2=?, V2=80 m³, T2=?
Vyberte jako pracovní látku vzduch a nastavte teplotu.

1. Nastavte parametry vzduchu v počátečním bodě 1
2. Vyplňte odpovídající hmotnost plynu m1 tlačítkem "◄"
3. Tlačítkem "►►" rozkopírujte hodnoty do ostatních bodů
4. Vyplňte koncový objem po stlačení V2
5. Zadejte požadovaný polytropický exponent n=1.2

6. Stisněte tlačítko "Polytr."
Dojde k výpočtu a doplnění parametrů p2 a T2, které vyhovují zadanému polytropickému exponentu n=1.2
7. Výsledky:
Koncový tlak p2 = 617 kPa
Koncová teplota T2 = 106.8 °C
Tlaková práce Wt = 62.2 MJ (17.27kWh)
Teplo odvedené do okolí Q=25.8 MJ
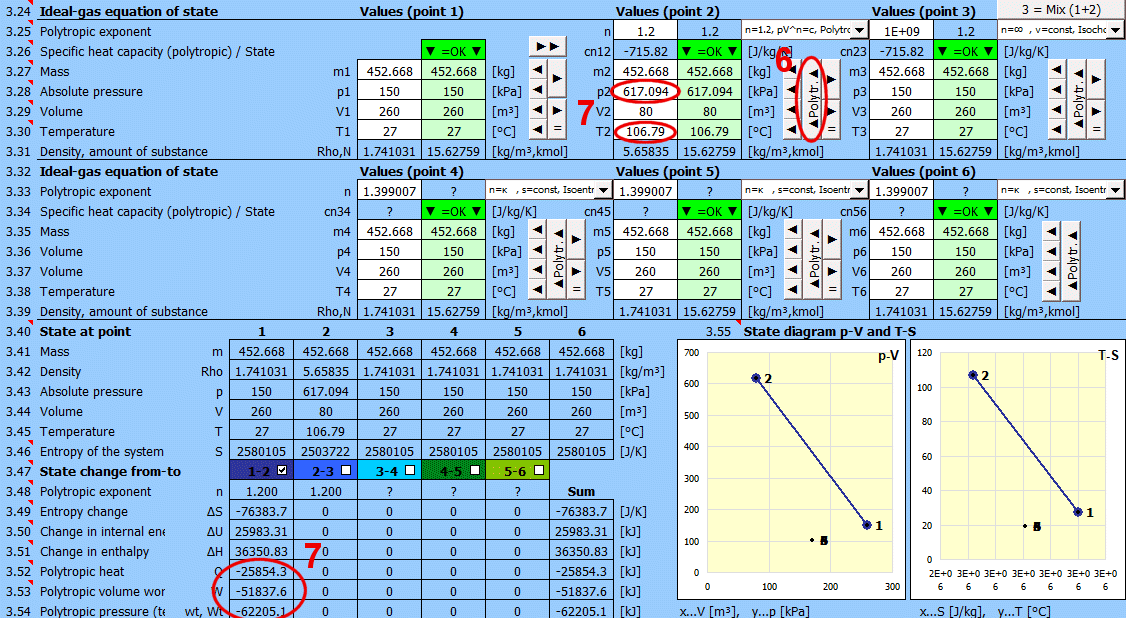
Výpočet pístového kompresoru (obsah 1 litr)
Pracovní látka: Vzduch
Pracovní objem: V1=0.001 m³
Polytropický exponent: n=1.3 (Pístový kompresor s částečným odvodem tepla,
typická hodnota pro pomalé kompresory s chlazením).
Sací tlak: p1=100kPa
Výtlačný tlak: p2=500kPa
Teplota nasávaného vzduchu: T1=25 °C
Škodlivý prostor X: 5% => V3 = 0.00005 m³ (Z konstrukčních důvodů není možné
úplné vytlačení plynu. Zbytkový plyn expanduje a snižuje objem nasávaného plynu).
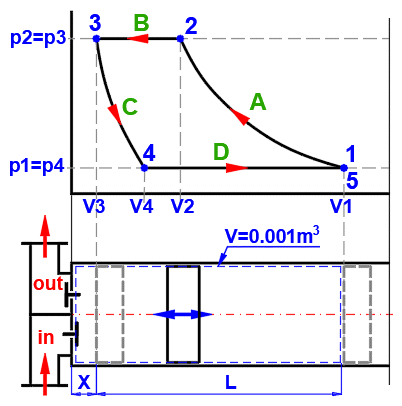
Vyberte jako pracovní látku vzduch a nastavte teplotu.
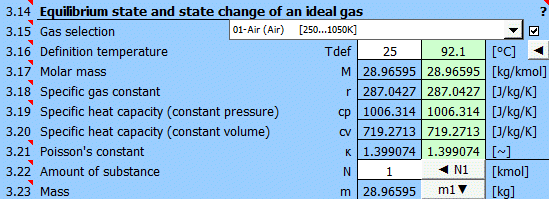
1. Nastavte parametry v bodě 1 (p1=100 kPa, V1=0.001 m³, T1=25 °C), vyplňte m1
tlačítkem "◄"
2. Tlačítkem "►►" rozkopírujte hodnoty do ostatních bodů
3. Zadejte výtlačný tlak p2=500kPa a polytropický exponent n=1.3
4. Stisněte tlačítko "Polytr."
Dojde k výpočtu a doplnění parametrů V2 a T2, které vyhovují zadanému polytropickému exponentu n=1.3
5. Zkopírujte výsledky do bodu 3 tlačítkem "►"
6. Zadejte koncový objem výtlaku V3 = 0.00005 m³ a vyplňte m3 tlačítkem "◄".
7. Zkopírujte výsledky do bodu 4 tlačítkem "►"
8. Zadejte sací tlak p4=100kPa a polytropický exponent n=1.3
9. Stisněte tlačítko "Polytr."
Dojde k výpočtu a doplnění parametrů V4 a T4, které vyhovují zadanému
polytropickému exponentu n=1.3.
Plyn expanduje do stavu p4=p1 (sací tlak).
10. Zkopírujte výsledky do bodu 5 tlačítkem "►"
11. Zadejte koncový objem sání V5 = 0.001 m³ a vyplňte m5 tlačítkem "◄".
12. Zapněte zobrazení stavu v diagramu p-V. (přechodové křivky jsou zobrazené
jako přímky)
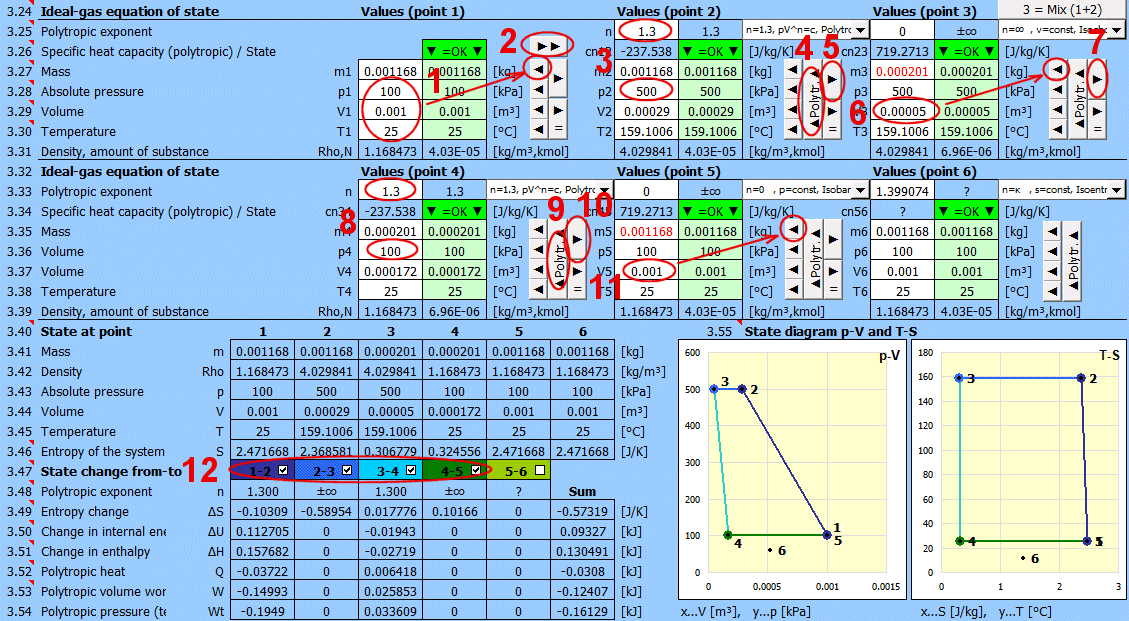
V ocelové trubce kruhového pruřezu o vnitřním průměru d=102mm, tlouštce stěny
3mm a délce L=200m proudí voda s teplotou T1=90°C o rychlosti v1=0.1m/s. Trubka
je opatřena izolací z minerální vaty o tloušťce 20mm, vnější vrstvou PVC o
tloušťce 1mm a natřena bílou barvou. Trubka je umístěna v exteriéru a vystavena
proudění vzduchu s teplotou T2=10°C s rychlostí v2=3m/s. Potrubí je
ozářené sluncem s intenzitou 1000W/m².
Vyřešte tepelnou ztrátu a teplotu vody na konci trubky.
1. Zadejte teplotu T1 a T2
2. Zvolte typ stěny
3. Postupně definujte vrstvy stěny (rozměry a fyzikální vlastnosti). Materiály je možné vybírat ze seznamu [4.7]
a přidávat tlačítkem Add.
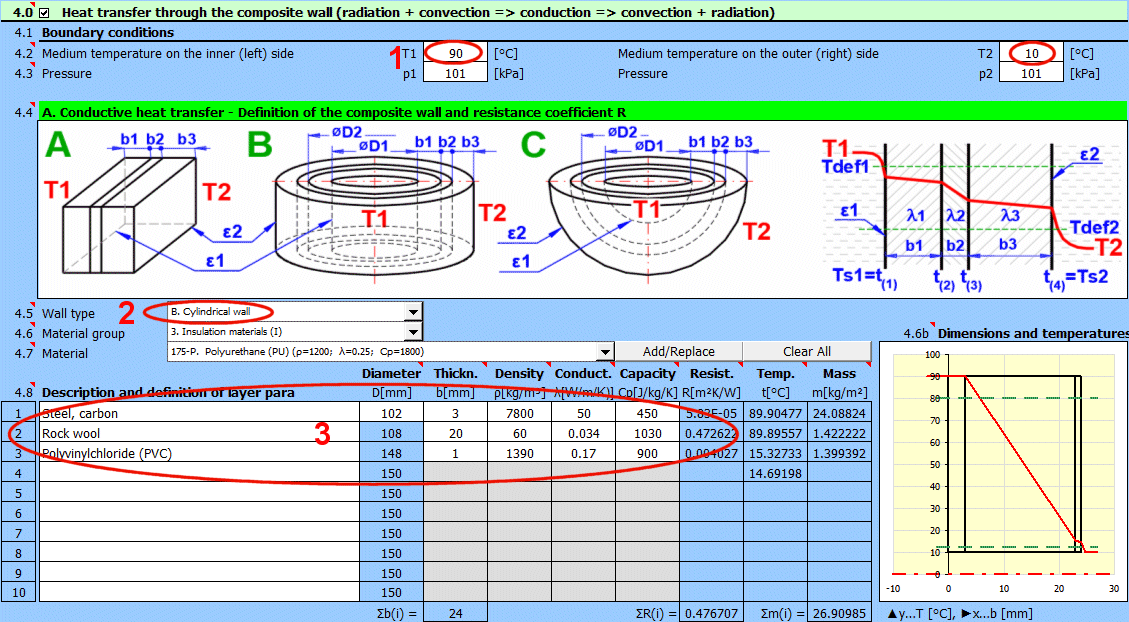
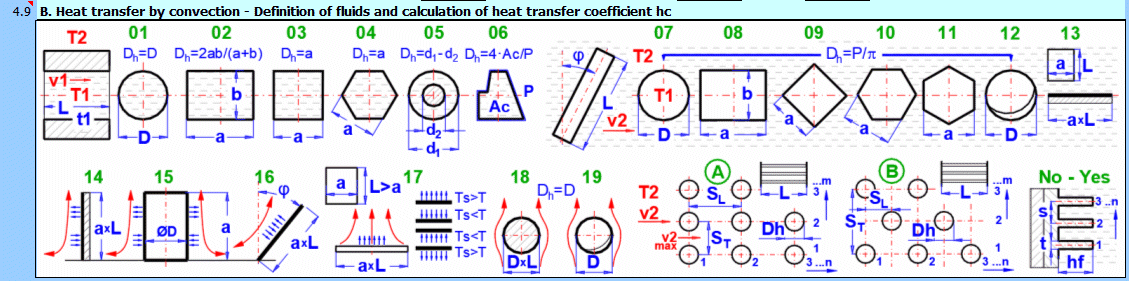
4. Vyberte pracovní médium 1 a 2.
5. Vyberte typ proudění = tvar obtékané plochy
6. Zadejte rychlost proudění a rozměry
7. Stiskněte tlačítko pro postupnou iteraci výsledků.
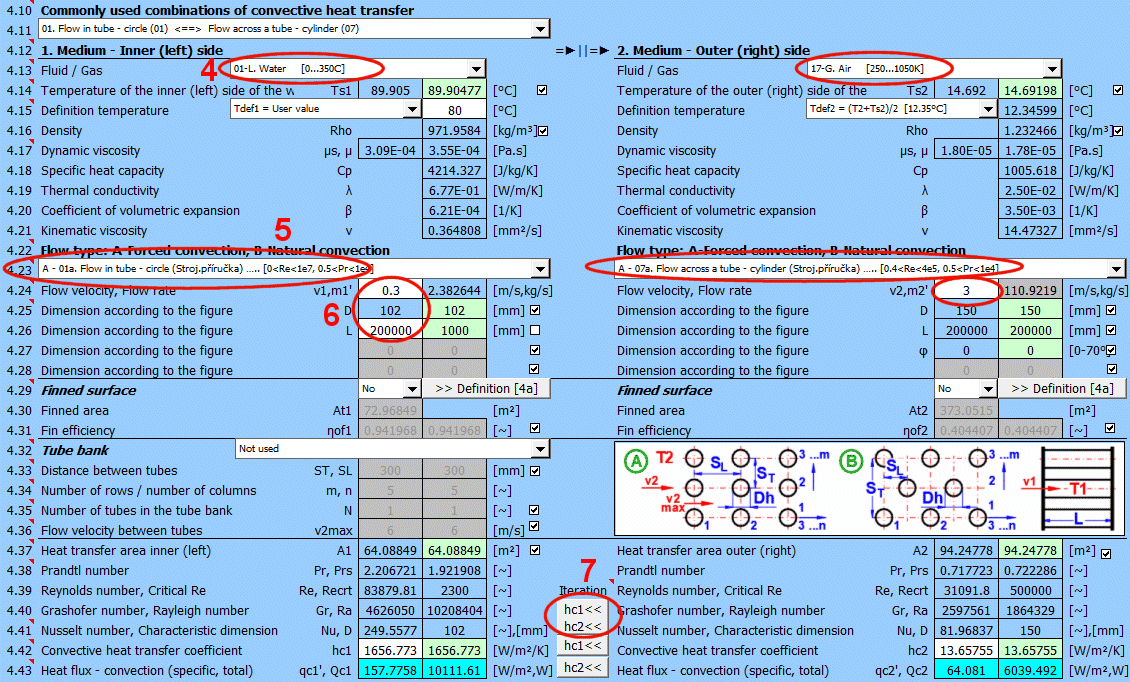
Řešíme uzavřený profil, není tedy nutné se zabývat zářením na vnitřní straně trubky (médium 1).
8. Vyberte typ povrchu, nebo zadejte přímo emisivitu ε2
na [4.45]
9. Vyberte vyzařování tepla do prostoru.
10. Zadejte sílu záření a z výběrového seznamu vyberte položku "*
ε" - je použita emisivita z [4.45]
11. Zvolte velikost ozářené plochy Ai2 vzhledem k ploše A2. (Slunce neozáří celý
povrch potrubí).
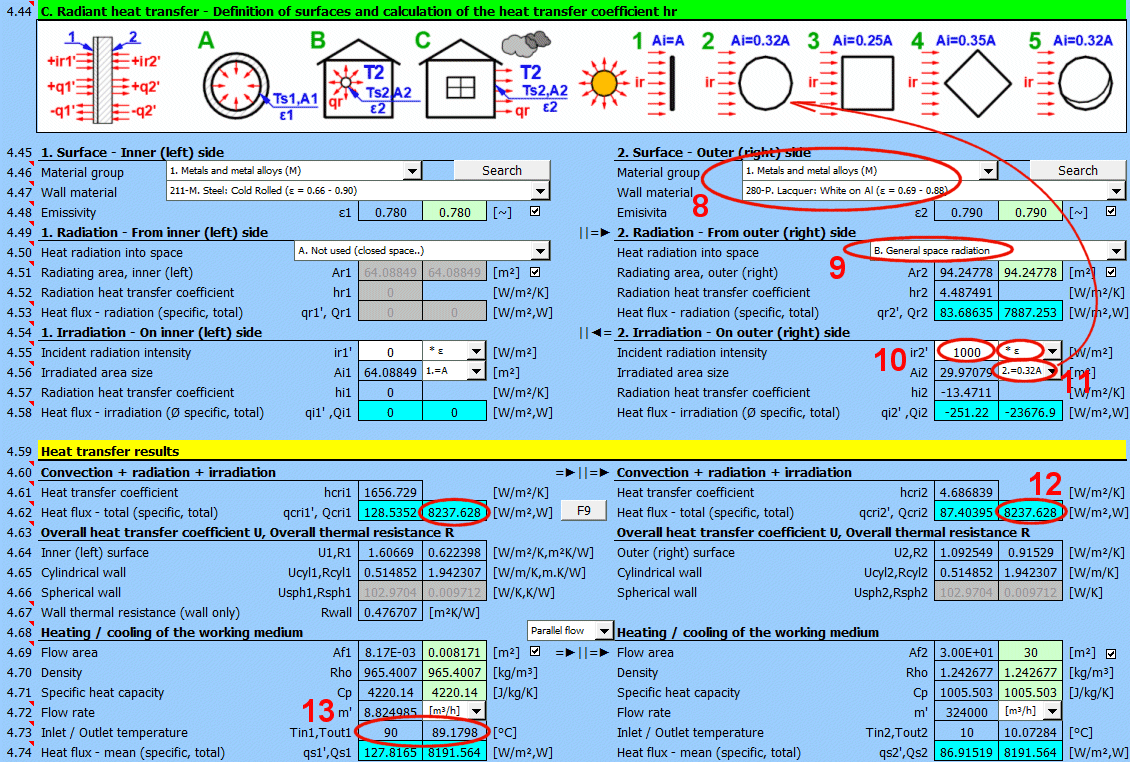
12. Výsledné ztráty jsou 8237W
13. Teplota na konci potrubí je přibližně 89.2°C
Zkuste měnit krycí nátěr (emisivitu ε2 [4.47, 4.48]) a to jak pro potrubí ozářené sluncem, tak i pro potrubí bez ozáření (ir2 = 0W/m² [4.51]).
1. Pojmenujte aktuální řešení přestupu tepla
2. Přidejte popis řešení
3. Přidejte aktuální řešení do seznamu na listu "Stěny"
4. Vyberte řešení ze seznamu uložených řešení.
5. Načtěte kompletní data. Aktuální hodnoty budou přepsané hodnotami z vybraného
řešení.

Řešení se ukládají do listu "Stěny". Jeden řádek obsahuje jedno uložené
řešení.
List "Stěny" je volně přístupný a je možné jej normálně editovat prostředky
excelu (například vymazání nepotřebných řešení - řádků).
Pokud potřebujete zjistit konkrétní hodnotu a použít ji ve vlastním vzorci, je připravená funkce GetWallProp, která to umožňuje.
Syntaxe:
GetWallProp(ID;value_name)
ID ... Číslo řádku na listu "Stěny", který obsahuje uložené řešení
value_name ... Jméno hodnoty, kterou chcete zjistit.
Příklad:
=GetWallProp(1;"Date") ... Vrátí datum, kdy bylo řešení přidané do seznamu
=GetWallProp(1;"T1") ... Vrátí teplotu média 1 - T1 ve [°C]
=GetWallProp(1;"U1") ... Vrátí hodnotu součinitele přestupu tepla U1 ve [W/m²/K]
Častou úlohou může být určení parametrů přestupu tepla, pokud znáte (například z měření) některé hodnoty a nechcete řešit kompletní přestup tepla stěnou.
Teplota obvodové zdi domu o výšce 3.5m a délce 20m byla termokamerou změřena na Ts1=3°C. Okolní vzduch má teplotu T1=0°C a proudí podél zdi rychlostí 3m/s.
Určete součinitel přestupu tepla U a celkový tepelný tok Q.
1. Zadejte teplotu proudícího vzduchu T1=0°C (Teplotu T2 je možné zvolit
libovolně)
2. Zvolte rovinnou stěnu
3. Zvolte nějaký materiál stěny (nezáleží na jeho parametrech)
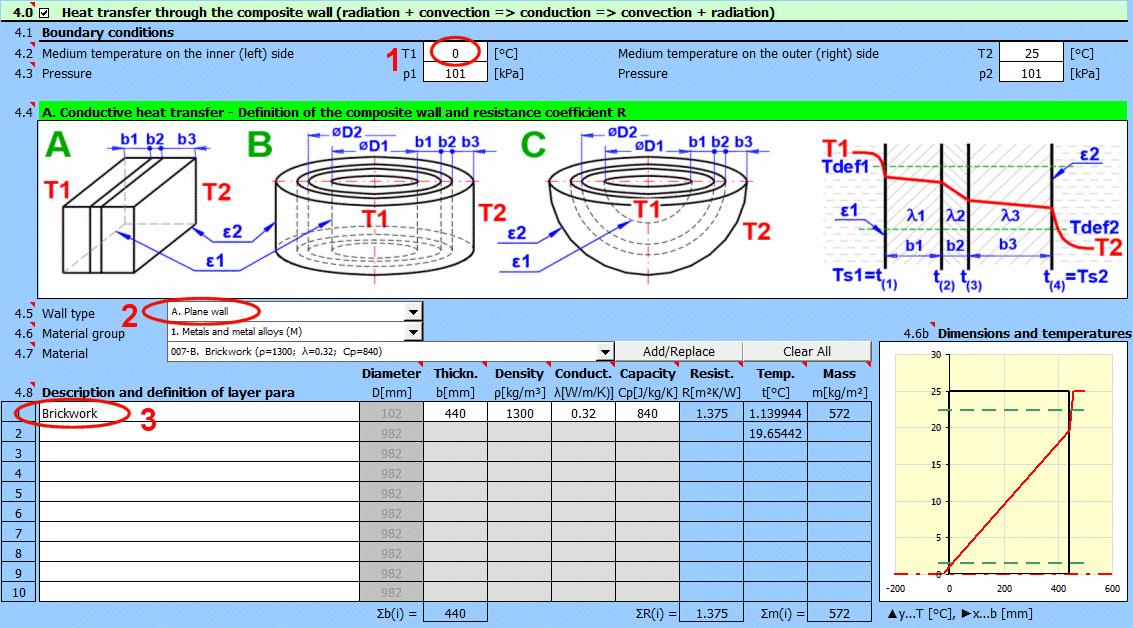
4. Zvolte jako pracovní médium vzduch
5. Odškrtněte automatické vyplnění teploty stěny Ts1. Tím dojde k přerušení
komplexního výpočtu a je řešena pouze levá strana stěny
6. Zadejte teplotu stěny Ts1=3°C
7. Vyberte nucené proudění okolo rovinné plochy
8. Zadejte rychlost proudění v1=3m/s
9. Zadejte rozměry plochy
10. Stisněte tlačítko pro iteraci hc1
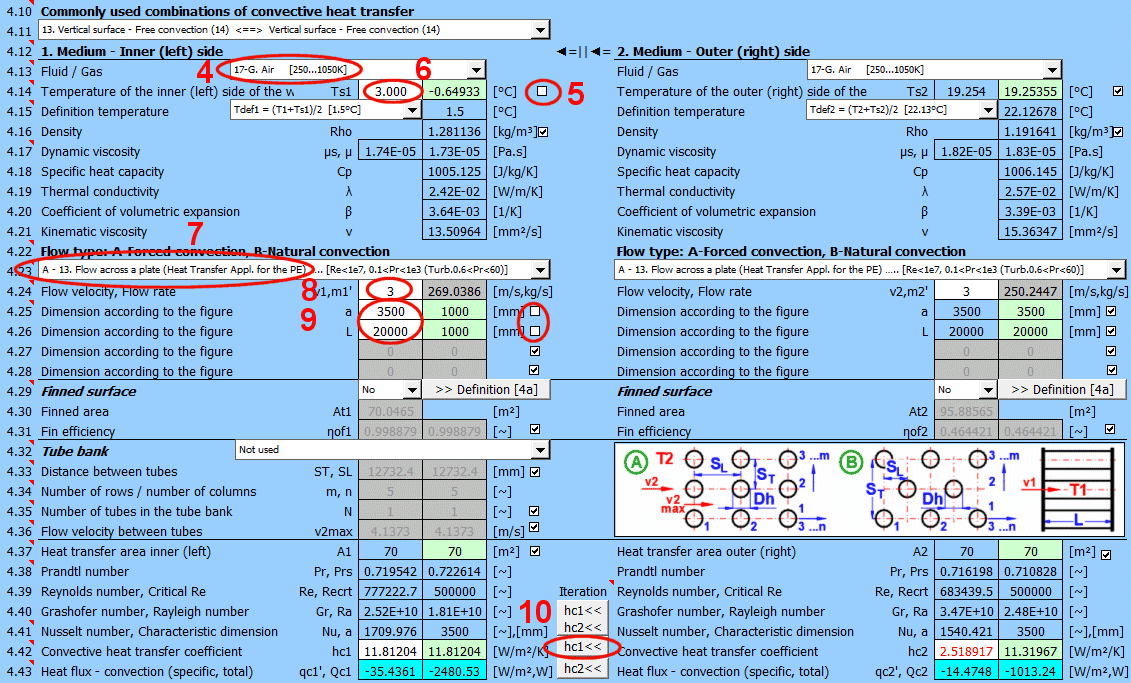
11. Zvolte povrchový materiál stěny
12. A nebo přímo zadejte emisivitu povrchu
13. Zvolte vyzařování v exteriéru
14. Získáte celkový tok tepla stěnou Q1 a součinitel přestupu tepla U1
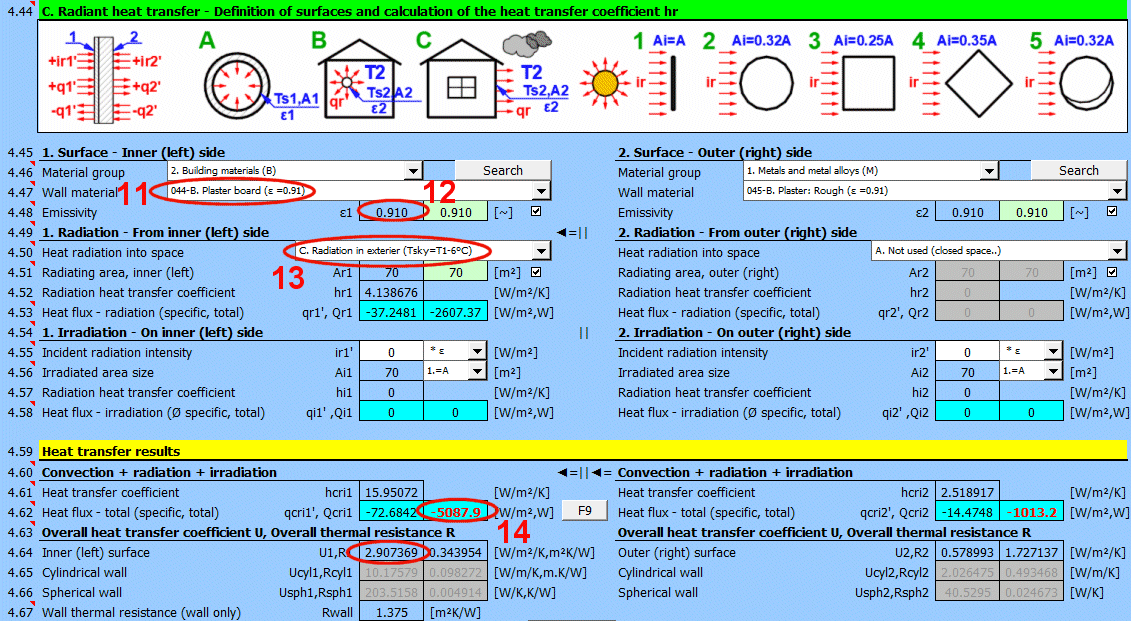
Zkuste měnit krycí nátěr (emisivitu ε2 [4.47, 4.48]).
Pro různé kryogenní nádrže, termosky atd. je často používána stěna s vakuuem na jedné straně.
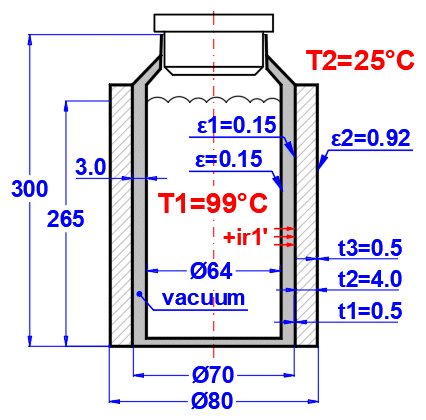
Termoska o objemu 0.85l má válcovou stěnu složenou z ocelového plechu t1=0.5mm, izolace t2=4.0mm a PVC obalu t3=0.5mm. Na vnitřní straně stěny je vakuum. Na vnější straně je vzduch o teplotě 25°C. Válcová stěna má vnitřní průměr D=70mm a výšku L=300mm. Uvnitř termosky je nádoba s vodou o teplotě 99°C. Tloušťka vakuua je 3mm. Záření na vnitřní stěnu je 45W/m² (Z výpočtu v odstavci [7.0]).
Určete součinitel přestupu tepla U a celkový tepelný tok Q.
Přijaté zjednodušení: Je řešen přestup tepla obvodové stěny, vliv dna je kompenzován použitím výšky 300mm.
1. Zadejte teploty T1=99°C a T2=25°C
2. Zvolte válcovou stěnu
3. Definujte jednotlivé vrstvy stěny
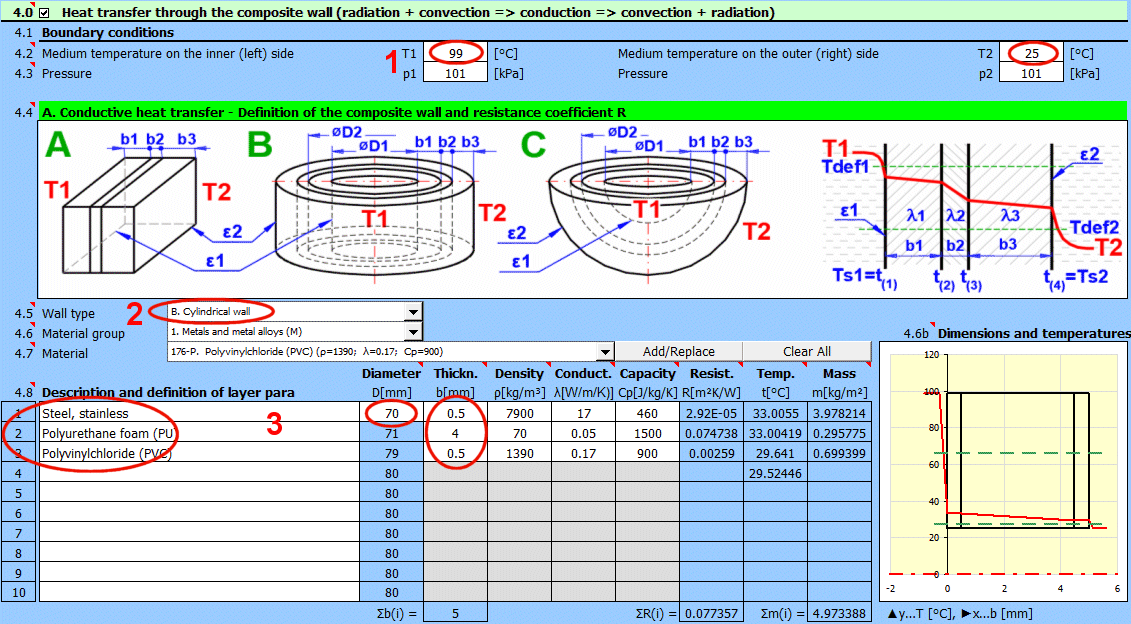

4. Vyberte pracovní médium 1 a 2
5. Vyberte typ proudění = tvar obtékané plochy
6. Zadejte rozměry obtékané nádoby
7. Stiskněte tlačítko pro postupnou iteraci výsledků
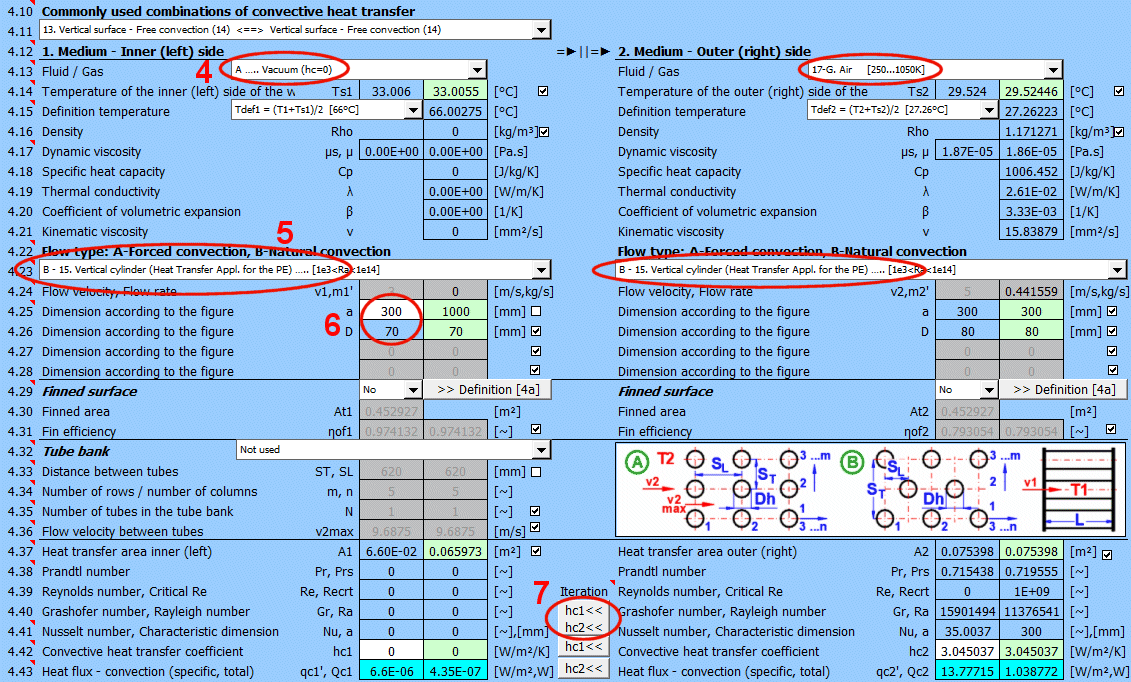
Je nutné vyřešit vyzařování do prostoru pro vnější povrch
8. Vyberte typ povrchu, nebo zadejte přímo emisivitu ε2=0.92
na [4.45]
9. Vyberte vyzařování tepla v interiéru
Ozáření vnitřního povrchu stěny.
10. Není řešené vyzařování do prostoru - je řešen uzavřený prostor
11. V odstavci [7.0] je vypočtena velikost záření ir1=45W/m²
(Příklad 18 níže)
pro emisivitu stěny ε1=0.15, zvolte tedy násobek "*
1"
12. Je ozářená celá vnitřní plocha, zvolte volbu "1.=A"
13. Hodnoty q,Q a U mohou být použité v dalších výpočtech (Příklad 15 níže)
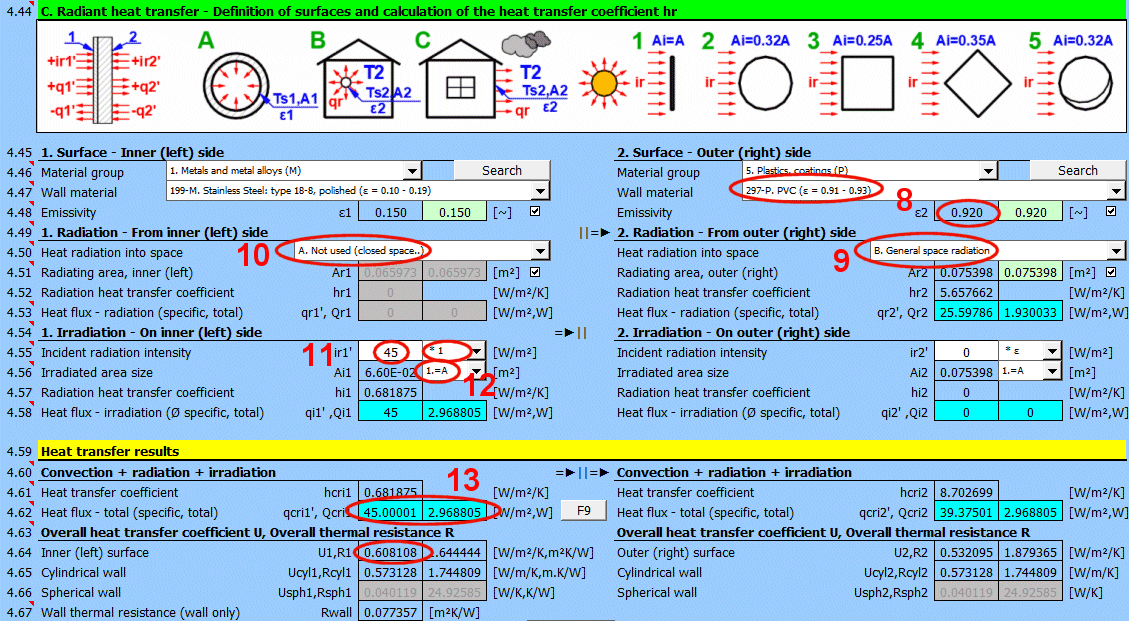
Analýza generátoru elektrického proudu s TEG články a s chladičem, který je chlazen vzduchem.
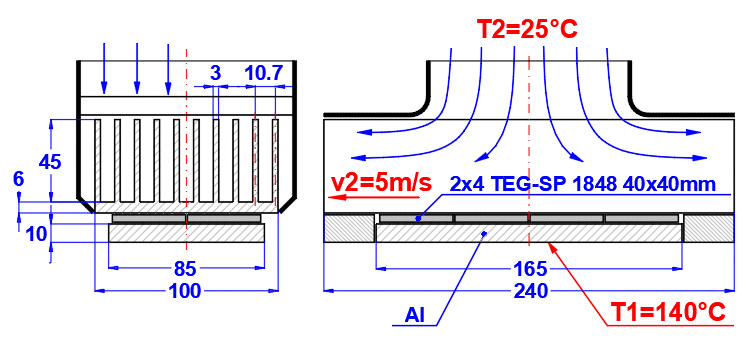
Osm TEG článků přiléhá jednou stranou na hliníkovou desku s rozměry 85x165x10 mm. Druhou stranou na hliníkový chladič s rozměry 100x240x51mm s deseti žebry a tloušťkou základny 6mm. Hliníková deska je kontaktně napojena na zdroj tepla o teplotě T1=140°C. Chladičem prochází vzduch o teplotě T2=25°C s rychlostí 5m/s. Tepelná vodivost TEG článku je 1.5 [W/m/K].
Zjistěte teplotu TEG článku na horké a studené straně.
1. Zadejte teploty T1=140°C a T2=25°C.
2. Zvolte rovinou stěnu.
3. Definujte jednotlivé vrstvy stěny podle obrázku.
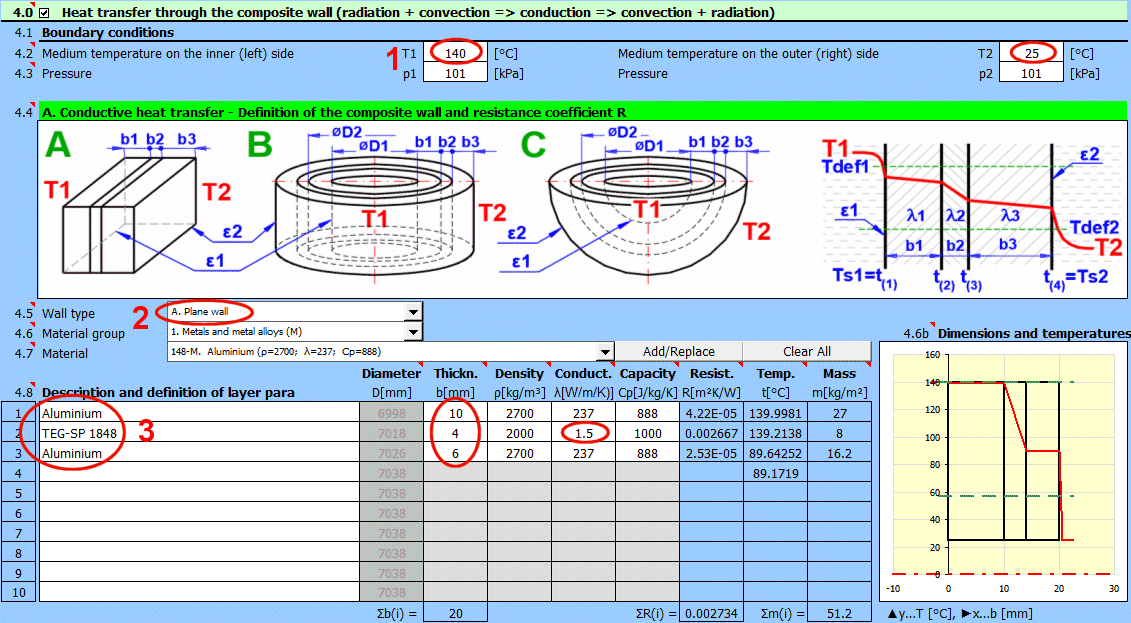

4. Vyberte pracovní médium 1 a 2 (Médium 1 - kontaktní spojení se zdrojem
tepla).
5. Zadejte rozměry kontaktní desky.
6. Zvolte typ proudění (Nucené obtékání desky = proudění vzduchu v chladiči).
7. Zadejte rozměry půdorysu chladiče a rychlost proudění vzduchu.
8. Zapněte použití žebrovaného povrchu a v odstavci [4a.0] definujte jeho
rozměry.
9. Po definici rozměrů žebrování stiskněte tlačítko pro postupnou iteraci
výsledků.
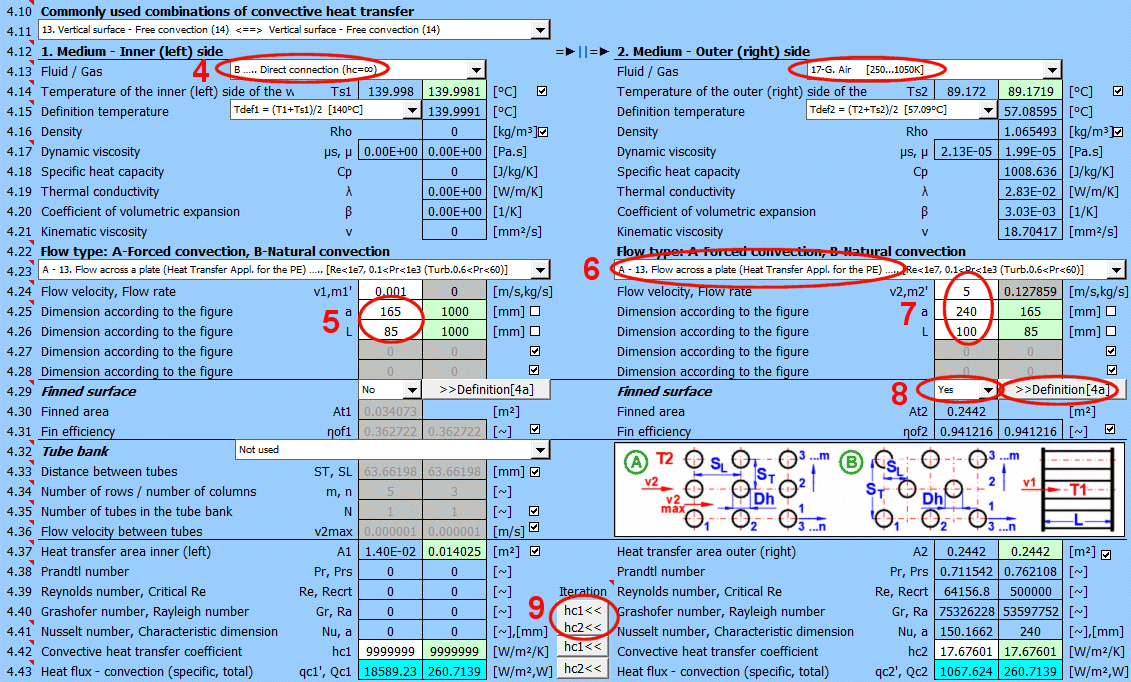
10. Zvolte obdélníkový tvar žebra.
11. Zadejte rozměry a počet žeber. Návrh na počet žeber je spočítán z šířky
žebrovaného pole [4a.5] a vzdáleností mezi žebry [4a.9].
12. Je spočítaná účinnost žebrování (použito pro výpočet koeficientu přestupu
tepla [4.29, 4.39].
13. Je spočítaná obtékaná plocha, která se zvětší žebrováním a je použita místo
původní hodnoty [4.34].
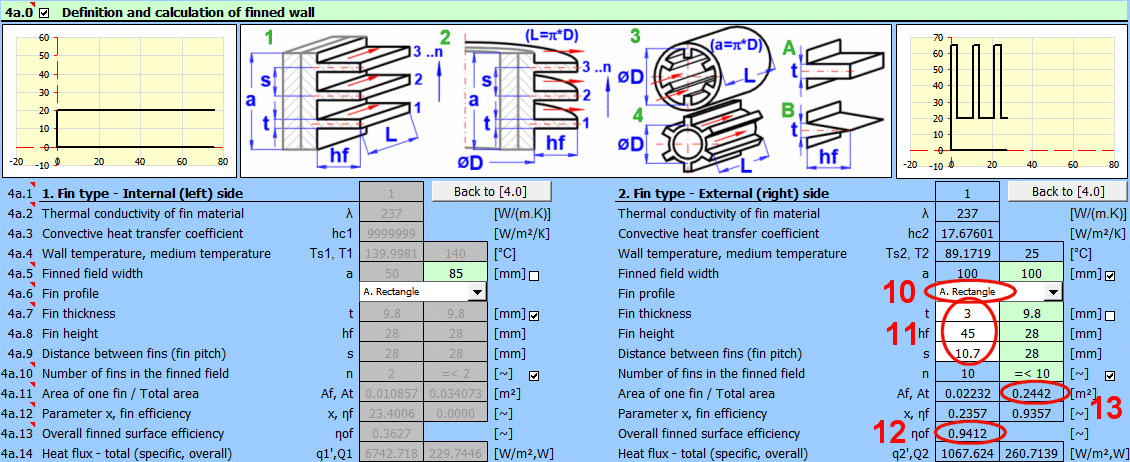
V tomto výpočtu není potřeba řešit záření, je nutné příslušně nastavit parametry.
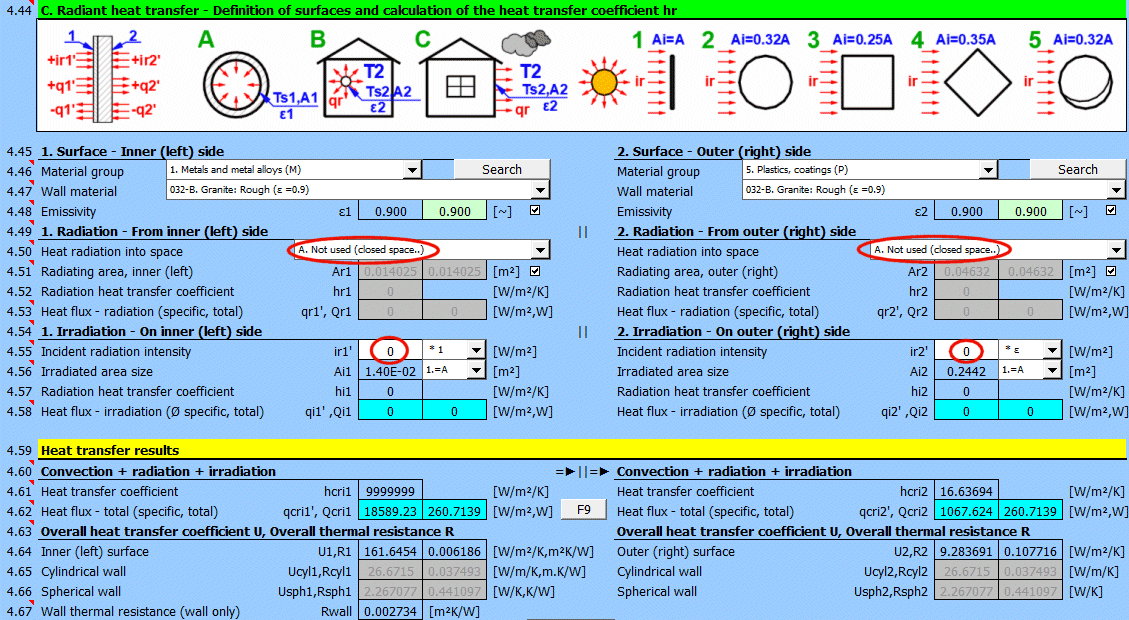
Požadované výsledky (teploty stěny TEG článku) zjistíte v tabulce [4.8].
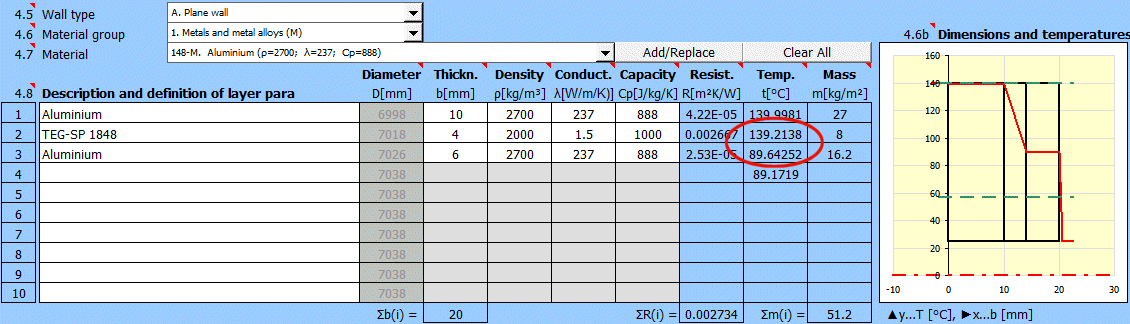
Závěr: Rozdíl teplot je 50°C. Z katalogových údajů pak pro tento teplotní rozdíl je výkon jednoho článku zhruba 1W, pro 8 článků pak 8W. Pro zvýšení teplotního rozdílu by tedy bylo nutné podstatně zvýšit plochu chladiče (více tenčích a vyšších žeber) a nebo použít například chlazení vodou.
Výpočet přestupu tepla ve svazku trubek.
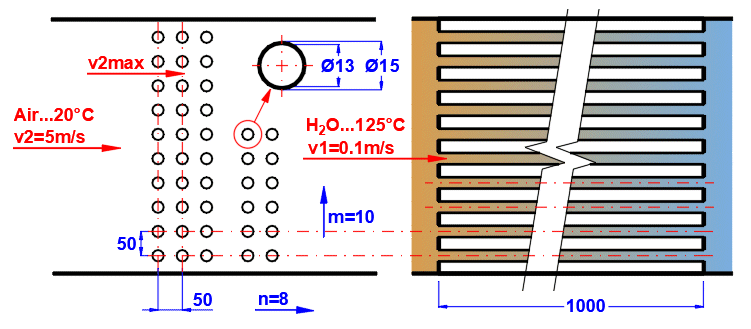
Voda z geotermálního vrtu o teplotě T1=125°C protéká trubkami rychlostí 0.1 m/s. Ocelové trubky jsou ve svazku 10 řad, 8 sloupců. Vnitřní průměr trubky D1=13mm, vnější průměr D2=15mm. Do svazku trubek vstupuje vzduch o teplotě T2=20°C rychlostí 5m/s.
Určete výstupní teplotu vzduchu a výkon výměníku.
1. Zadejte teploty T1=125°C a T2=20°C.
2. Zvolte válcovou stěnu.
3. Definujte rozměry a materiál trubky.
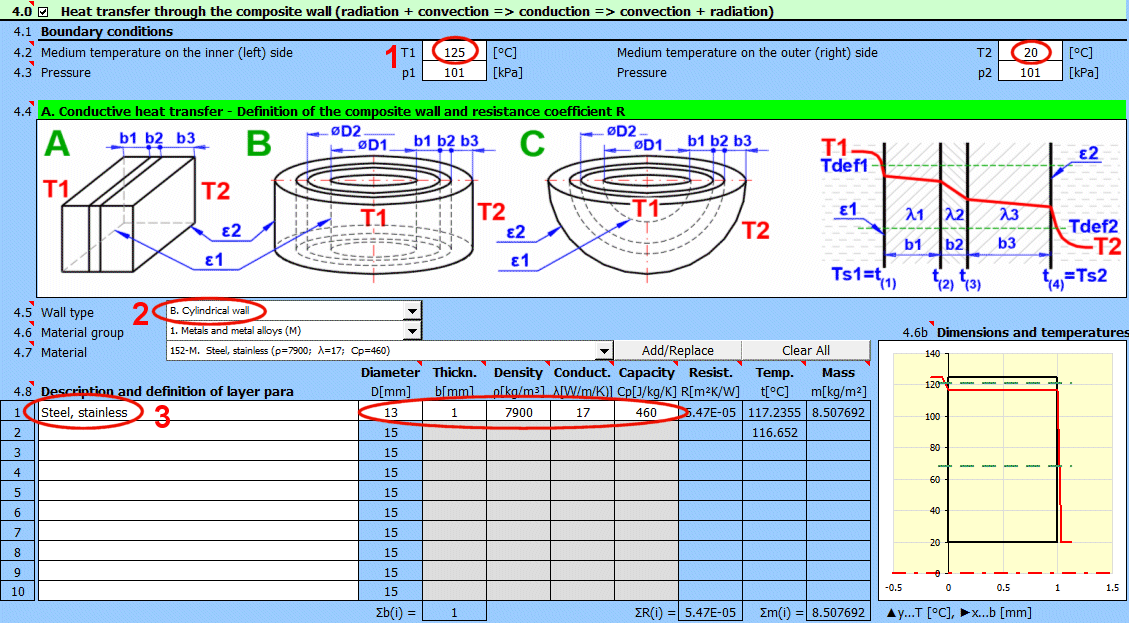

4. Vyberte pracovní médium 1 a 2.
5. Vyberte typ proudění (Voda protéká trubkou, Vzduch obtéká trubku).
6. Zadejte rychlosti proudění a vnitřní a vnější rozměry trubky.
7. Zapněte a vyberte rozložení trubek ve svazku.
8. Zadejte vzdálenosti mezi trubkami a jejich počet podle obrázku.
9. Po definici rozměrů stiskněte tlačítko pro postupnou iteraci
výsledků.
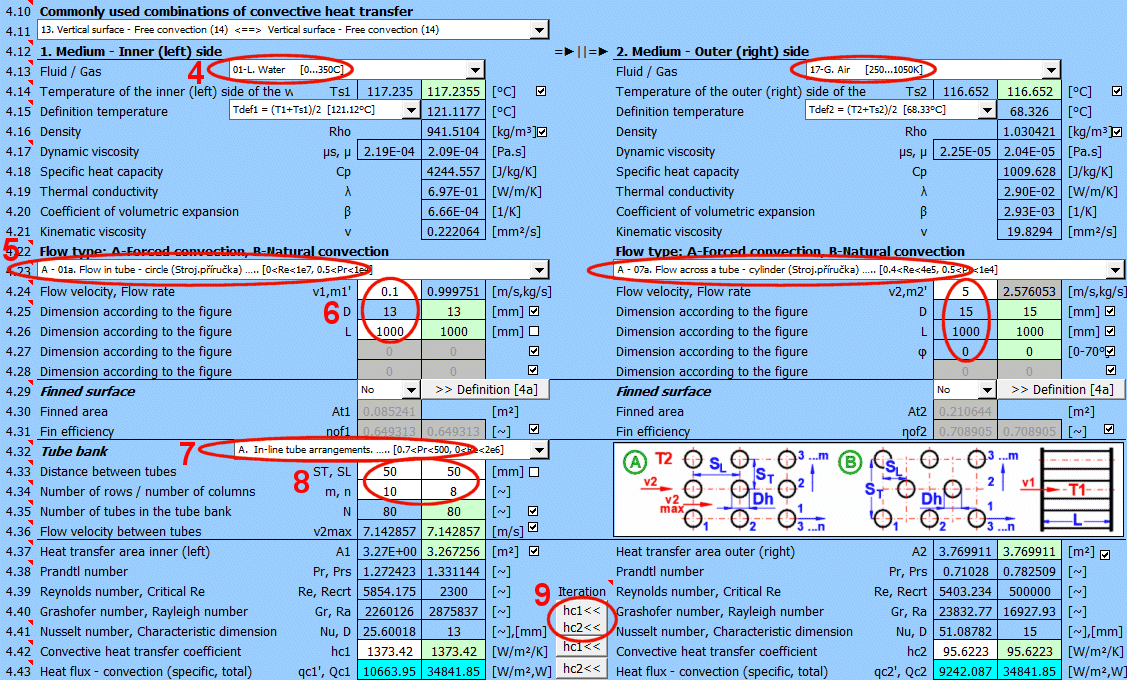
V tomto výpočtu není potřeba řešit záření, je nutné příslušně nastavit parametry.
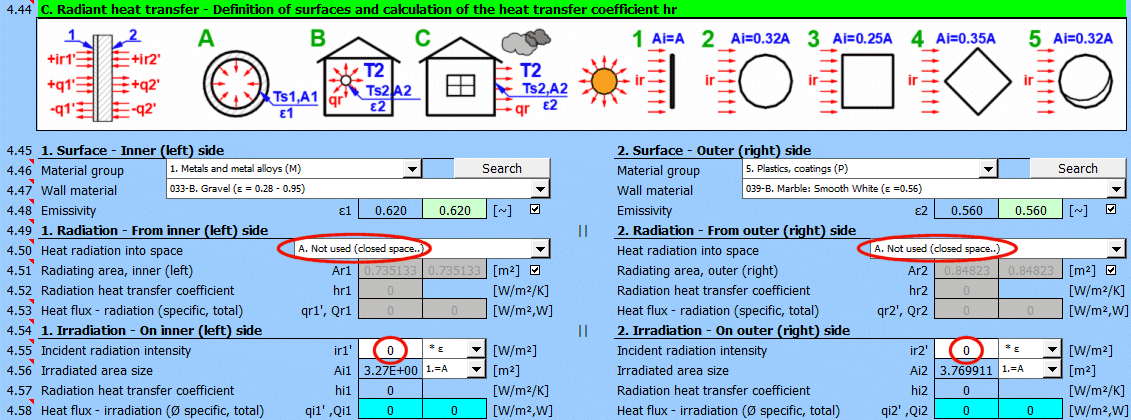
10. Zvolte typ vzájemného proudění - Protiproud (Více možností je v kapitole
Výměníků tepla).
11. Při zaškrtnutí tlačítka jsou použité přednastavené hodnoty Af, Rho, Cp.
Program se je snaží navrhnout na základě výše zadaných hodnot.
12. Pokud vám přednastavené hodnoty nevyhovují, můžete po odškrtnutí tlačítka
(11) zadat vlastní hodnoty.
13. Výstupní teplota vzduchu je 30.5°C a výkon necelých 32kW.
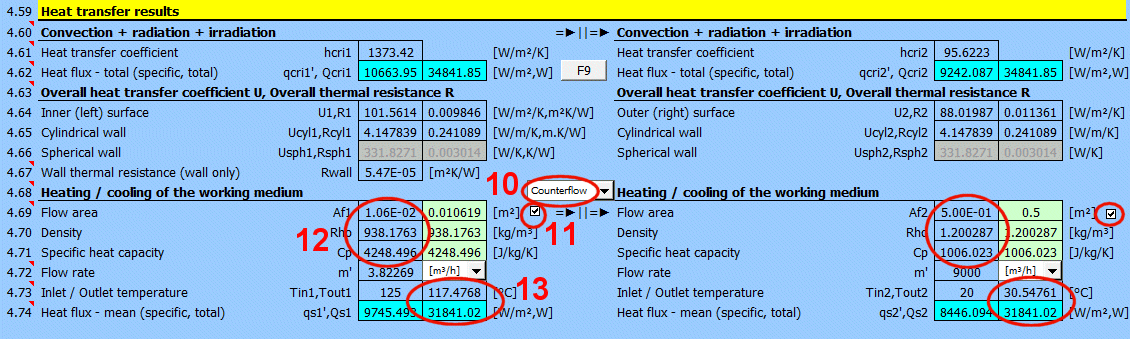
Závěr: Zvýšení teploty vzduchu o 10°C je poměrně nízké. Pro výměník tepla voda-vzduch by bylo jednoznačně výhodnější použít žebrování.
V předchozím příkladu byly použité trubky bez žebrování. V tomto příkladu použijeme méně trubek s větším rozměrem a se žebrováním.
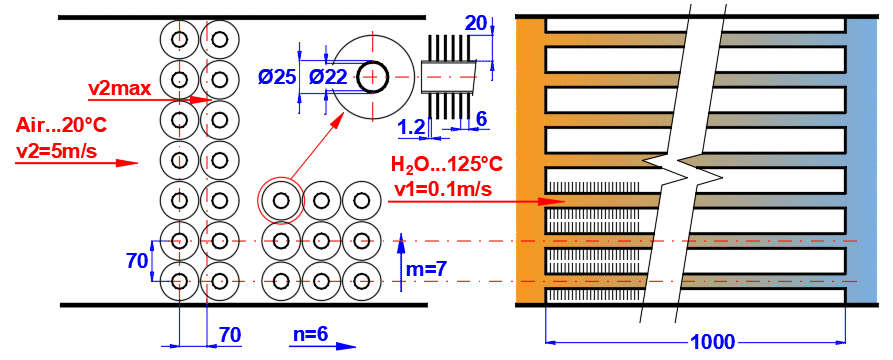
Voda z geotermálního vrtu o teplotě T1=125°C protéká trubkami rychlostí 0.1 m/s. Ocelové trubky jsou ve svazku 7 řad, 6 sloupců. Vnitřní průměr trubky D1=22mm, vnější průměr D2=25mm. Do svazku trubek vstupuje vzduch o teplotě T2=20°C rychlostí 5m/s. Trubky jsou opatřené žebry. Tloušťka žebra t=1.2mm, výška žebra hf=20mm a rozteč s=6mm. Je použit max. počet žeber n=167.
Určete výstupní teplotu vzduchu a výkon výměníku.
1. Zadejte teploty T1=125°C a T2=20°C.
2. Zvolte válcovou stěnu.
3. Definujte rozměry a materiál trubky.
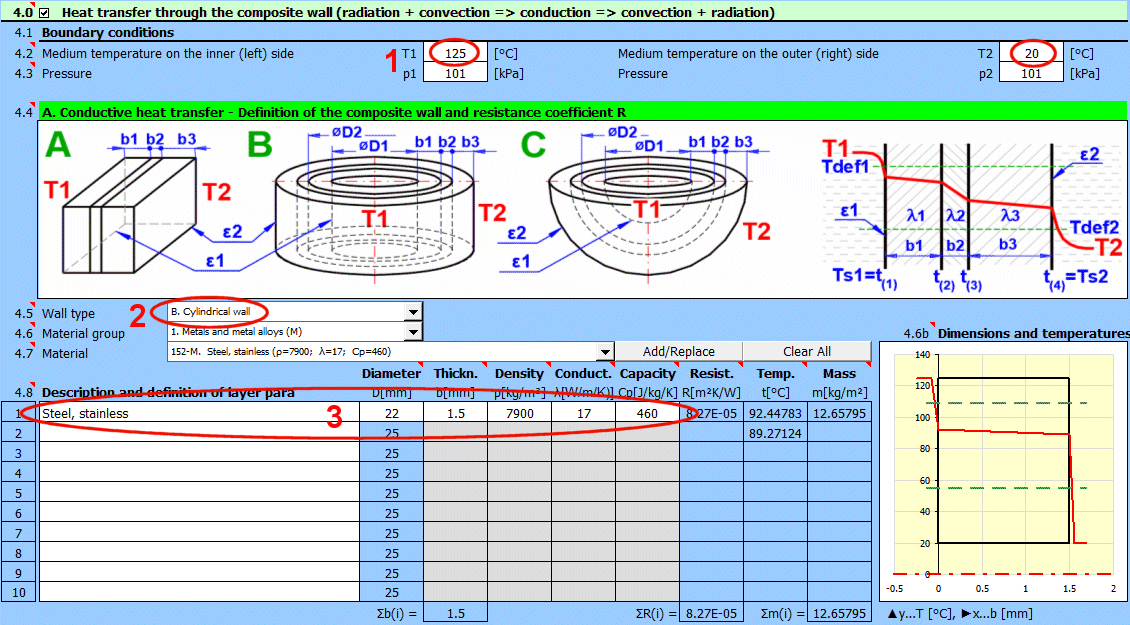

4. Vyberte pracovní médium 1 a 2.
5. Vyberte typ proudění (Voda protéká trubkou, Vzduch obtéká trubku).
6. Zadejte rychlosti proudění a vnitřní a vnější rozměry trubky.
7. Zapněte použití žebrovaného povrchu a v odstavci [4a.0] definujte jeho
rozměry.
8. Zapněte a vyberte rozložení trubek ve svazku.
9. Zadejte vzdálenosti mezi trubkami a jejich počet podle obrázku.
10. Po definici rozměrů stiskněte tlačítko pro postupnou iteraci
výsledků.
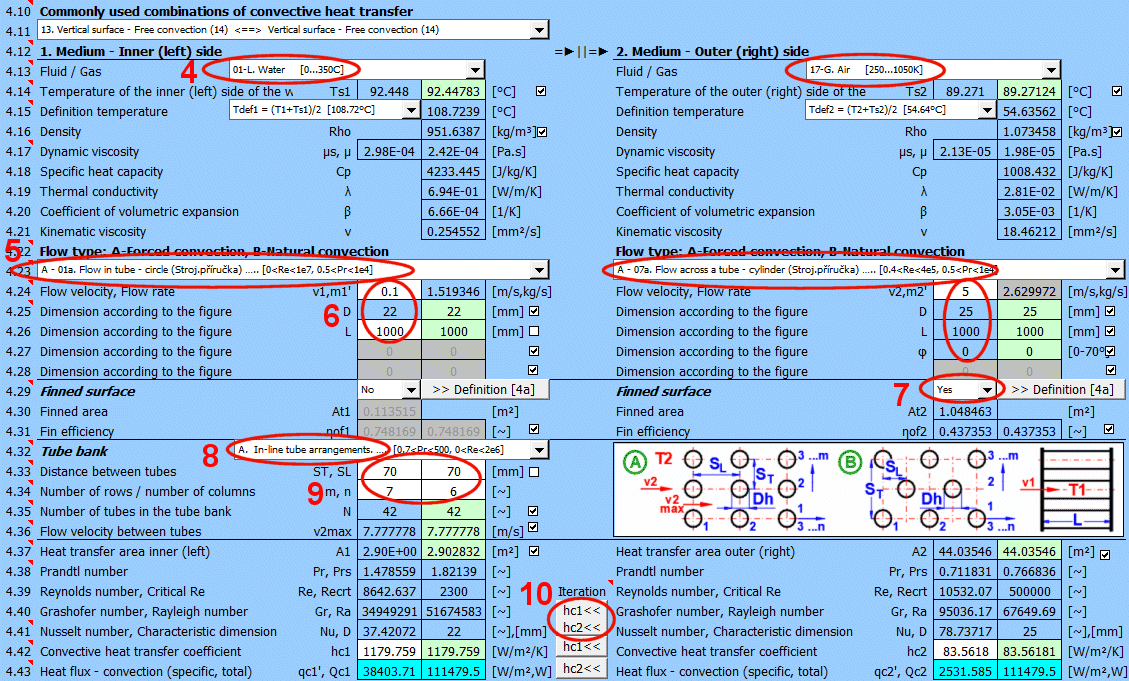
11. Zvolte obdélníkový tvar žebra.
12. Zadejte rozměry a počet žeber. Návrh na počet žeber je spočítán z šířky
žebrovaného pole [4a.5] a vzdáleností mezi žebry [4a.9].
13. Je spočítaná účinnost žebrování (použito pro výpočet koeficientu přestupu
tepla [4.29, 4.39].
14. Je spočítaná obtékaná plocha, která se zvětší žebrováním a je použita místo
původní hodnoty [4.34].
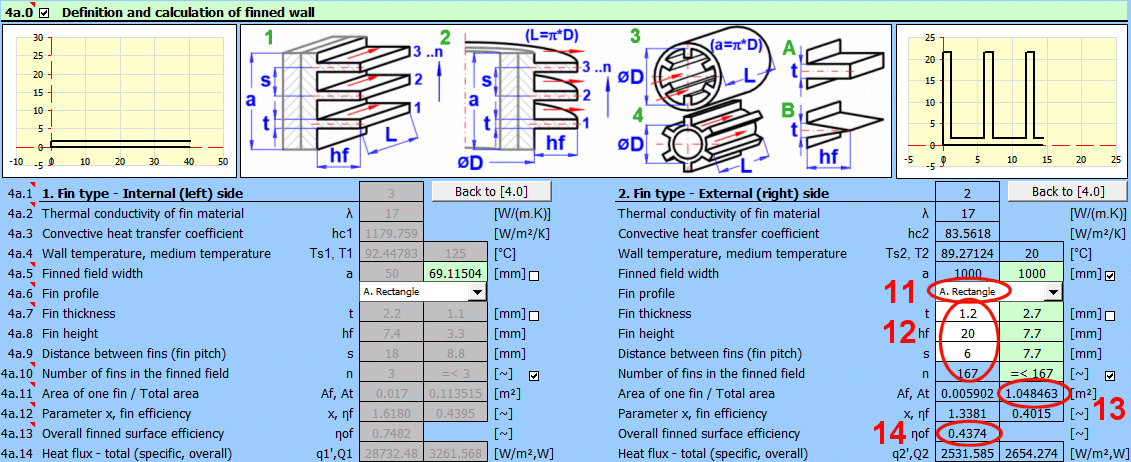
V tomto výpočtu není potřeba řešit záření, je nutné příslušně nastavit parametry.
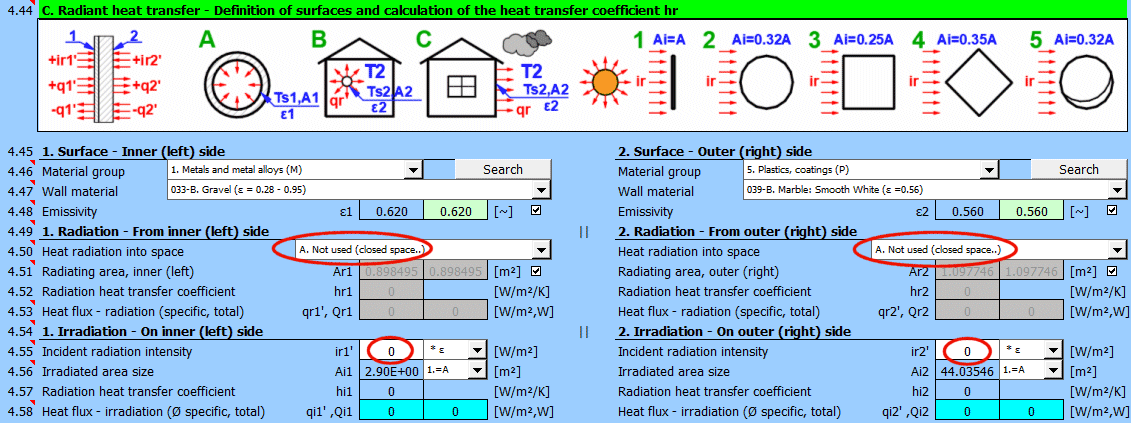
15. Zvolte typ vzájemného proudění - Protiproud (Více možností je v kapitole
Výměníků tepla).
16. Při zaškrtnutí tlačítka jsou použité přednastavené hodnoty Af, Rho, Cp.
Program se je snaží navrhnout na základě výše zadaných hodnot.
17. Pokud vám přednastavené hodnoty nevyhovují, můžete po odškrtnutí tlačítka
(16) zadat vlastní hodnoty.
18. Výstupní teplota vzduchu je 49.8°C a výkon 88kW.
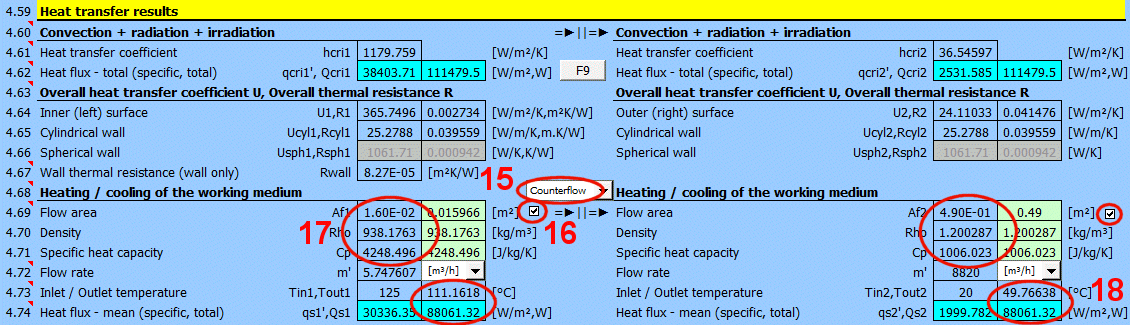
Závěr: Zvýšení teploty vzduchu o 30°C je proti předchozímu příkladu trojnásobné, při polovičním počtu trubek.
Z příkladu 11 známe součinitel přestupu tepla U=0.6081 [W/m²/K] a vnitřní plochu A=0.0659 [m²]. Počáteční teplota kapaliny (voda) T1s=99°C. Teplota okolí T2=25°C. Hmotnost kapaliny je 0.85kg.

Určete dobu ochlazení kapaliny z teploty T1s=99°C na teplotu T1e=39°C.
1. Ze seznamu vyberte kapalinu. Pokud kapalina není v seznamu, odškrtněte
tlačítko a zadejte hodnoutu Cp.
2. Zaškrtněte / odškrtněte tlačítko. Při zaškrtnutí jsou použité aktuální hodnoty z
odstavce [4.0]
3. Vyplněnte požadované vstupní hodnoty.
4. Doba chladnutí na 39°C je 41.5 hodiny. Což odpovídá uživatelským testům
termosek střední cenové kategorie.
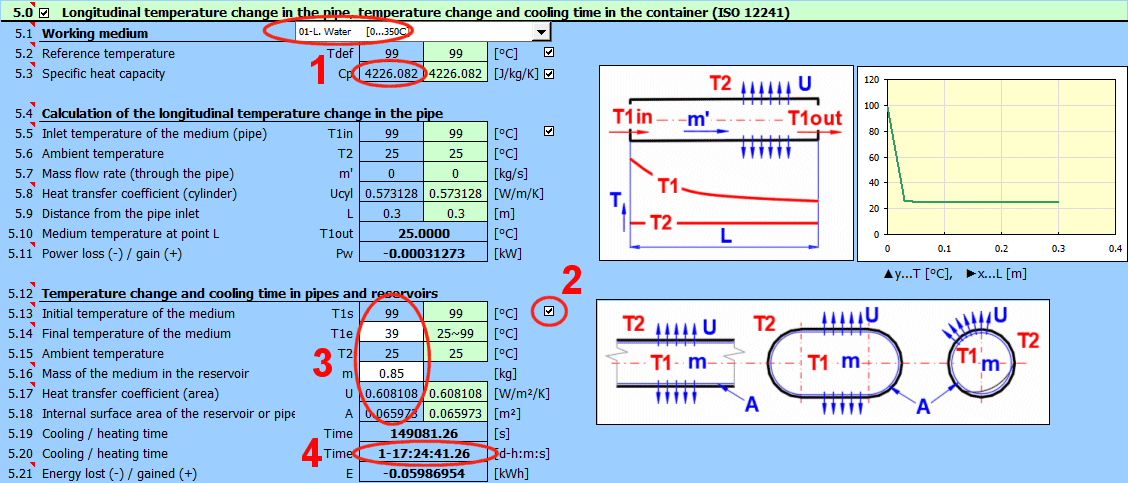
Pro chlazení oleje je použit trubkový výměník tepla. Hmotnostní tok chladící vody ve vnitřní trubce je m1'=0.25kg/s, hmotnostní tok oleje ve vnějším prstencovém průřezu je m2'=0.15kg/s. Voda vstupuje do výměníku s teplotou T1in=20°C, olej s teplotou T2in=98°C. Součinitel prostupu tepla válcovou stěnou je 3.25 W/m/K.
Je požadována výstupní teplota oleje T2Out=62°C. Určete výstupní teplotu vody a délku výměníku pro protiproudý trubkový výměník.
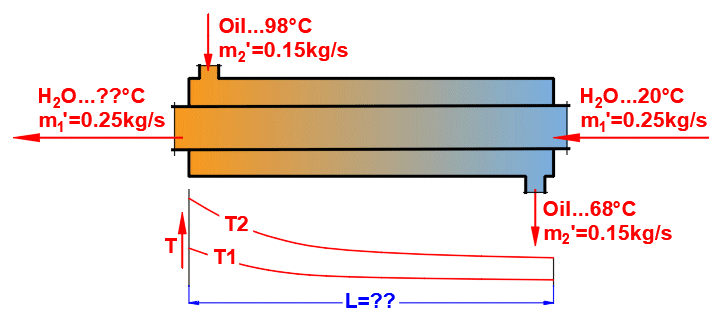

1. Vyberte typ výměníku.
2. Pokud se rozhodnete načíst data z definice stěny z odstavce [4.0], vyberte
příslušnou definici a načtěte tlačítkem "Load".
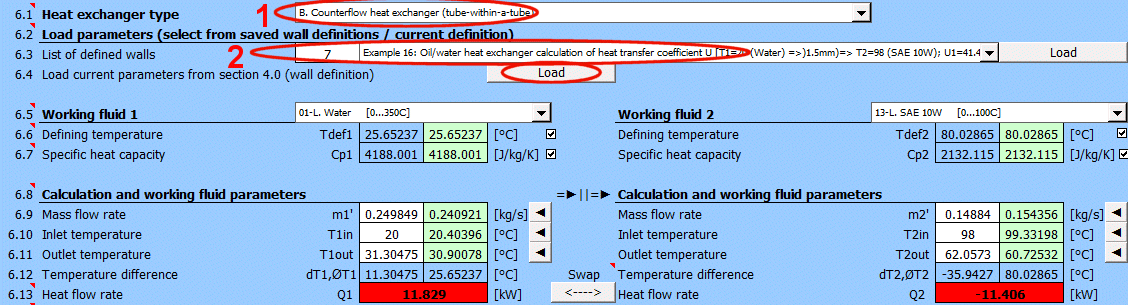
3. Vyberte pracovní médium 1 a 2. Pokud v seznamu není, zadejte přímo hodnotu Cp
[6.7].
4. Zadejte parametry média 1
5. Zadejte parametry média 2
Hodnoty Q1 a Q2 [6.13] budou s největší pravděpodobností rozdílné a označené
červeně. Je nutné vyřešit energetickou bilanci. V zelených polích jsou
vypočítané hodnoty, které při použití zajistí že Q1=-Q2.
6. Stiskněte tlačítko, kterým přenesete návrhovou hodnotu do T1Out. Výstupní
teplota vody T1Out=31°C.
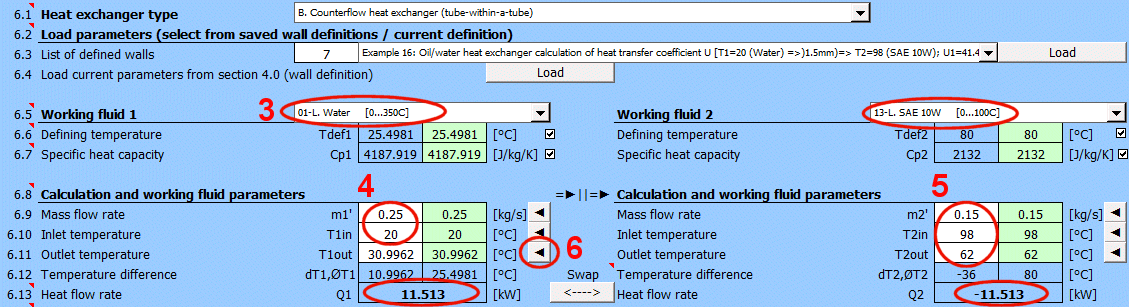
Po vyřešení energetické bilance je možné řešit délku trubky (nebo plochy).
7. Vyberte typ výpočtu B. V tomto případě řešíte délku výměníku a znáte Ucyl
[W/m/K].
8. Zadejte hodnotu součinitele přestupu tepla pro trubku Ucyl. Pokud jste
načetli hodnoty z výpočtu stěny (2), je tato hodnota v zeleném poli.
9. Výsledek výpočtu délky je L=66m.
10. Pokud znáte průměr trubky, můžete přepočítat délku na velikost teplosměnné
plochy.
11. Pokud chcete do výpočtu zahrnout i znečištění výměníku během provozu,
zadejte koeficient znečištění Rf a snižte
hodnotu Ucyl [6.21] o 4% [6.36].
12. Tlačítkem "▲U" nastavíte opravenou hodnotu Ucyl. Délka trubky pro výměník
zahrnující znečištění je pak L=69m.
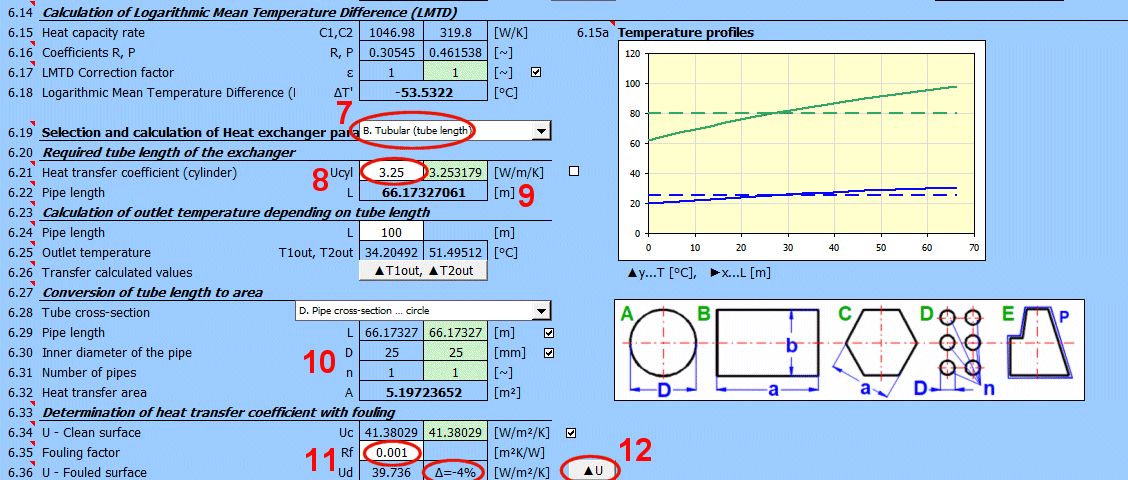
Chlazení vody v automobilovém chladiči. Radiátor je tvořen 40ti trubkami o
vnitřním průměru D1=5mm a délce L=650mm, které prochází skrz těsně uspořádané
tenké desky.
Voda vstupující do výměníku má teplotu T1in=90°C a
výstupní teplotu T1Out=65°C. Průtok vody je m1'=0.6kg/s.
Vzduch má na vstupu do výměníku T2in=20°C a výstupní teplotu T2Out=40°C.
Vyřešte průtok vzduchu výměníkem m2'=??, Výkon Q=?? a součinitel přestupu tepla U=??, kterého musí být dosaženo, aby byl splněn rozměrový požadavek 40trubek o délce 650mm.
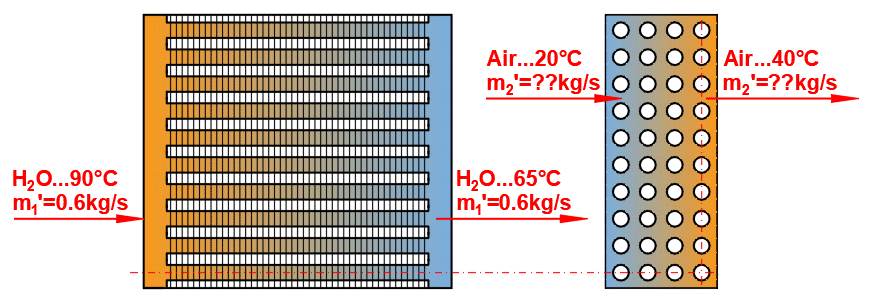

1. Vyberte typ výměníku.
2. Pokud se rozhodnete načíst data z definice stěny z odstavce [4.0], vyberte
příslušnou definici a načtěte tlačítkem "Load".
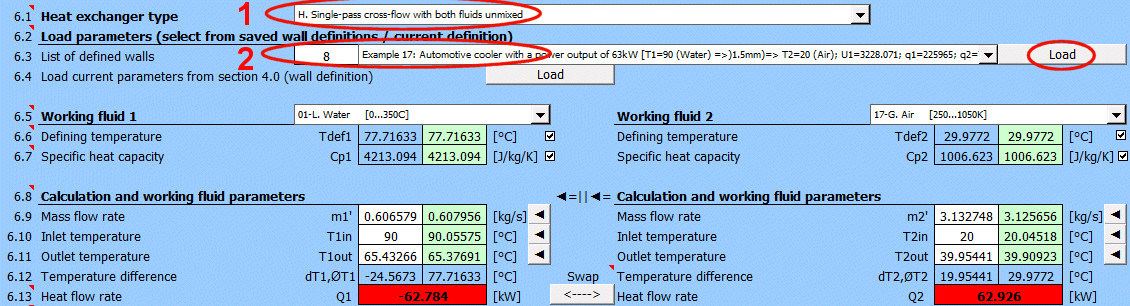
3. Vyberte pracovní médium 1 a 2. Pokud v seznamu není, zadejte přímo hodnotu Cp
[6.7].
4. Zadejte parametry média 1
5. Zadejte parametry média 2
Hodnoty Q1 a Q2 [6.13] budou s největší pravděpodobností rozdílné a označené
červeně. Je nutné vyřešit energetickou bilanci. V zelených polích jsou
vypočítané hodnoty, které při použití zajistí že Q1=-Q2.
6. Stiskněte tlačítko, kterým přenesete návrhovou hodnotu do m2'.
Průtok chladícího vzduchu m2'=3.14kg/s
Chladící výkon radiátoru je 63kW.
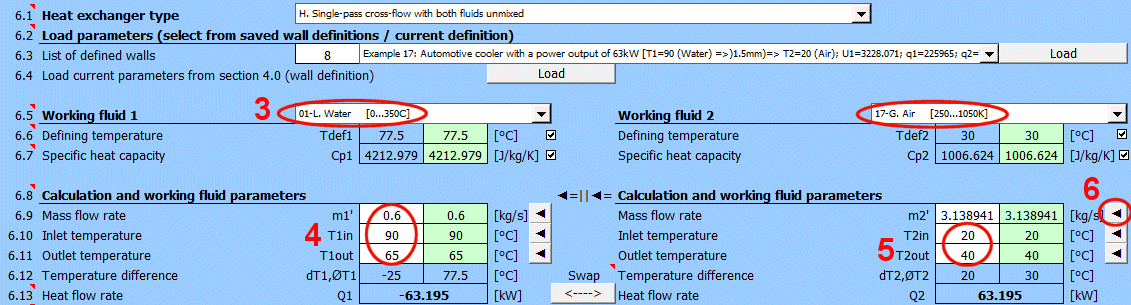
Po vyřešení energetické bilance je možné řešit potřebný součinitel přestupu
tepla. A to buď plošný Upl [W/m²/K], vztažený na jednotku vnitřní plochy trubek
a nebo součinitel vztažený na délku trubky Ucyl [W/m/K]. V tomto případě zvolíme
řešení pomocí plochy (A).
Výpočet plochy. A = D1 * Pi * L * n = 0.005 * 3.14159 * 0.65 * 40 = 0.4084m².
7. Pro výměníky typu C-H je nutné použít korekční koeficient
ε. Koeficient je
navržen ze vstupních a výstupních teplot automaticky.
8. Vyberte typ výpočtu A. V tomto případě je nutné určit Upl [W/m²/K] pro
dosažení definované plochy A.
9. Postupně měňte hodnotu Upl, dokud nebude dosažena odpovídající velikost
plochy A = 0.4084m².
10. Správnou velikost můžete ověřit konverzí plochy A na délku trubky.
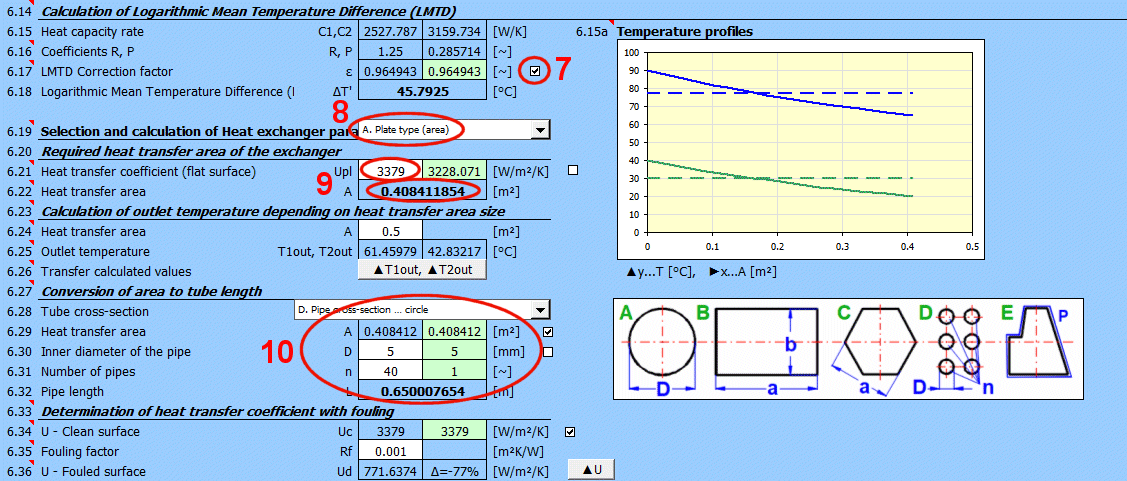
V příkladu 11 potřebujeme zjistit vzájemný tepelný tok mezi dvěma koncentrickými válci mezi nimiž je vakuum. Teplota stěny vnitřního válce T1=99°C, teplotu stěny vnějšího válce odhadneme na T2=30°C

Určete měrný tepelný tok q21, který je nutné znát pro řešení příkladu 11.
1. Zvolte dvě paralelní plochy.
2. Vyberte typ povrchu, nebo zadejte přímo emisivitu
ε1=ε2=0.15
na [7.5].
3. Zadejte teplotu T1=99°C
4. Zadejte teplotu T2=30°C (první odhad)
5. Zadejte rozměry válcových ploch
6. Výsledný měrný tepelný tok q21=47[W/m²].
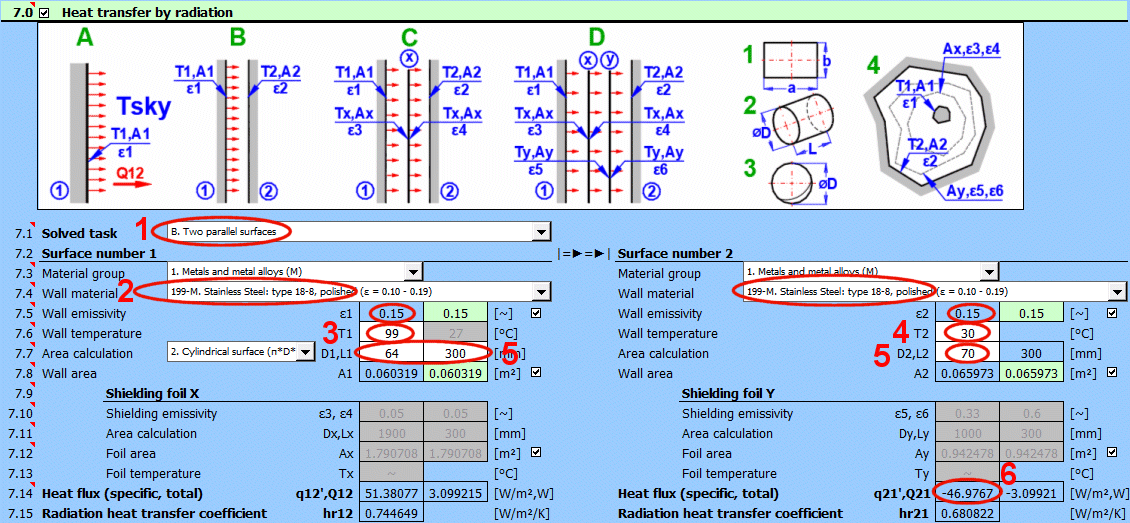
Po dosazení hodnoty q21=47 [W/m²] ve výpočtu přestupu tepla stěnou v odstavci
[4.0] zjistíme přesnou teplotu stěny T2=33°C.
Po zpětném dosazení T2=33°C do tohoto výpočtu získáme přesnější hodnotu q21=45
[W/m²].
Potrubí o průměru D1=200mm, povrchové teplotě T1=200°C a emisivitě
ε1=0.93 je umístěné koncentricky v kruhovém tunelu o průměru D2=2000mm,
povrchové teplotě T2=20°C a emisivitě
ε2=0.736. Stínění mezi povrchy je provedeno tenkou hliníkovou fólií
umístěnou koncentricky o emisivitě
ε3=ε4=0.05. Určete tepelný tok mezi potrubím a tunelem na 1m jeho délky.
A) Bez stínění.
B) Stínící fólie má průměr Dx=300mm
C) Stínící fólie má průměr Dx=1900mm

1. Vyberte typ řešené úlohy
2. Zadejte emisivitu povrchu 1 a 2
3. Zvolte typ řešené plochy
4. Zadejte teplotu a rozměry plochy 1 (potrubí). Zadejte délku 1m.
5. Zadejte teplotu a průměr kruhového tunelu (délka je stejná)
6. Tepelný tok na 1m potrubí Q=1370W
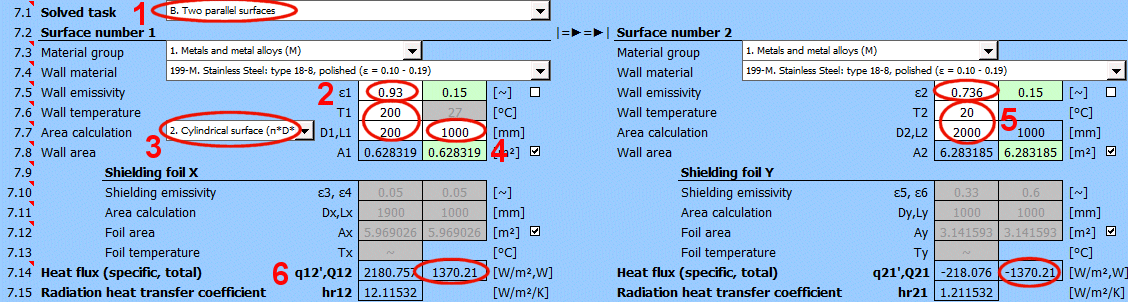
Hodnoty pro stěnu 1 a 2 zůstanou stejné
1. Změnte typ řešené úlohy na C
2. Zadejte emisivitu fólie
ε3, ε4
3.
Zadejte průměr stínící fólie Dx=300mm
4. Tepelný tok na 1m potrubí Q=56W
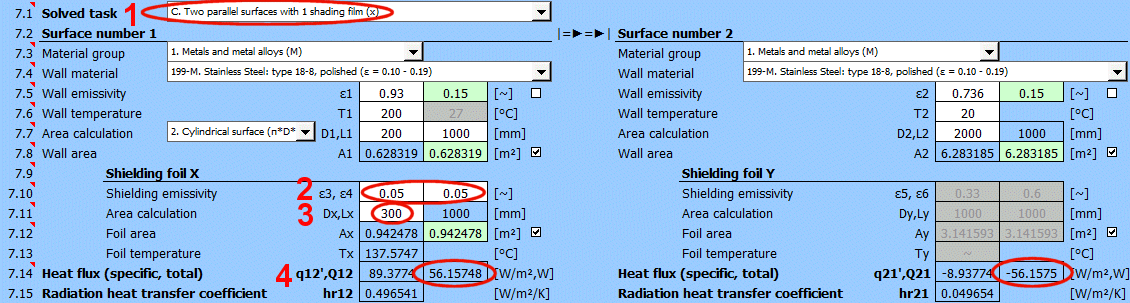
Hodnoty pro stěnu 1 a 2 zůstanou stejné, mění se pouze průměr Dx.
1. Zadejte průměr stínící fólie Dx=1900mm
2. Tepelný tok na 1m potrubí Q=292W

Závěr: Použití stínící fólie může být učinným prostředkem pro snížení přestupu tepla.
Projektujete potrubí, kterým bude proudit chladící kapalina. Vaše poloha je poblíž Paříže v průmyslové oblasti. Potřebujete zjistit maximální sluneční tepelné záření a celkový denní příkon.
1. Maximální intenzita slunečního záření je 21.6. ve 12.00
2. Zeměpisná šířka Paříže je ζ = 48.9°
3. Nastavte naklonění plochy kolmo na slunce β=30°
4. Nastavte orientaci plochy na jih γ=0°
5. Nadmořská výška Paříže je Alt=35m
6. Součinitel znečištění vzduchu v průmyslové oblasti Z=5
7. Maximální úroveň slunečního záření pro bezoblačnou oblohu pro zvolené
podmínky.
8. Celkový denní příkon na rovinnou definovanou plochu (v bodě 3 a 4). Příkon na válcovou
plochu bude o něco větší.
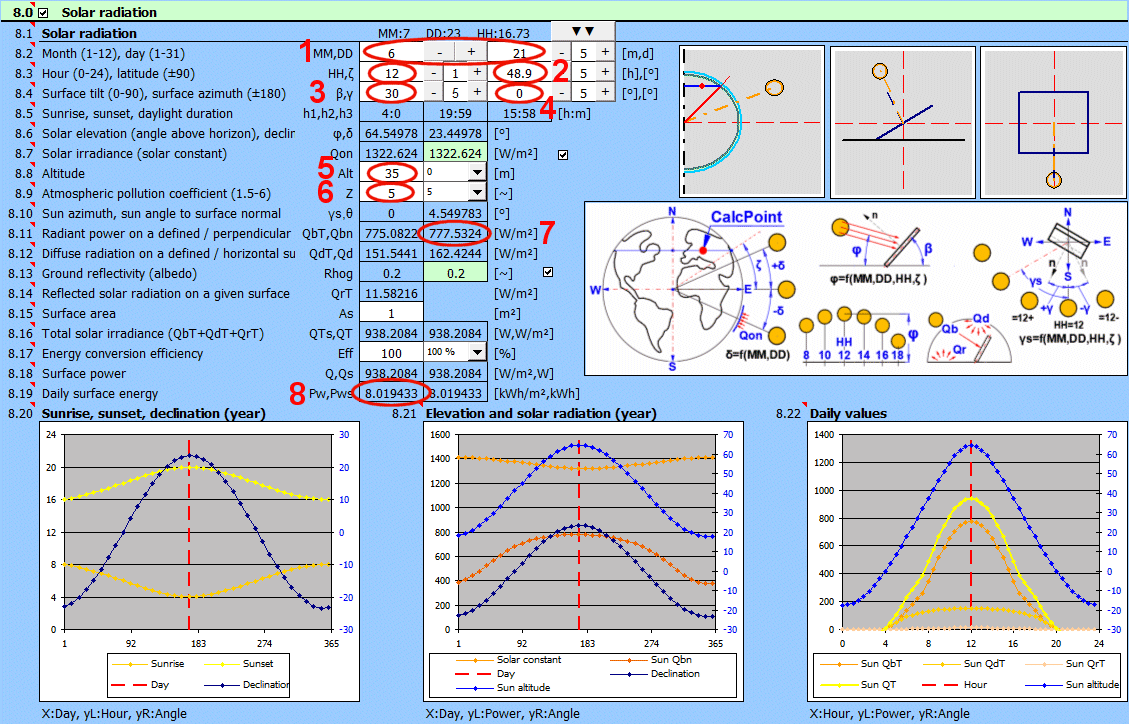
V servisní budově s plochou střechou (půdorys 5x14m).
Plochy stěn: Definované v obrázku
Součinitele přestupu tepla: Definované v tabulce
Vnější podmínky: T4=-10°C, vítr 10m/s
Požadované teploty a podmínky: T1=12°C, T2=22°C, T3=15°C
Vstupní podmínky: zdroje tepla QH1=1000W, QH2=2000W, QH3=1500W
Obě úlohy je možné řešit se stejným matematickým modelem.
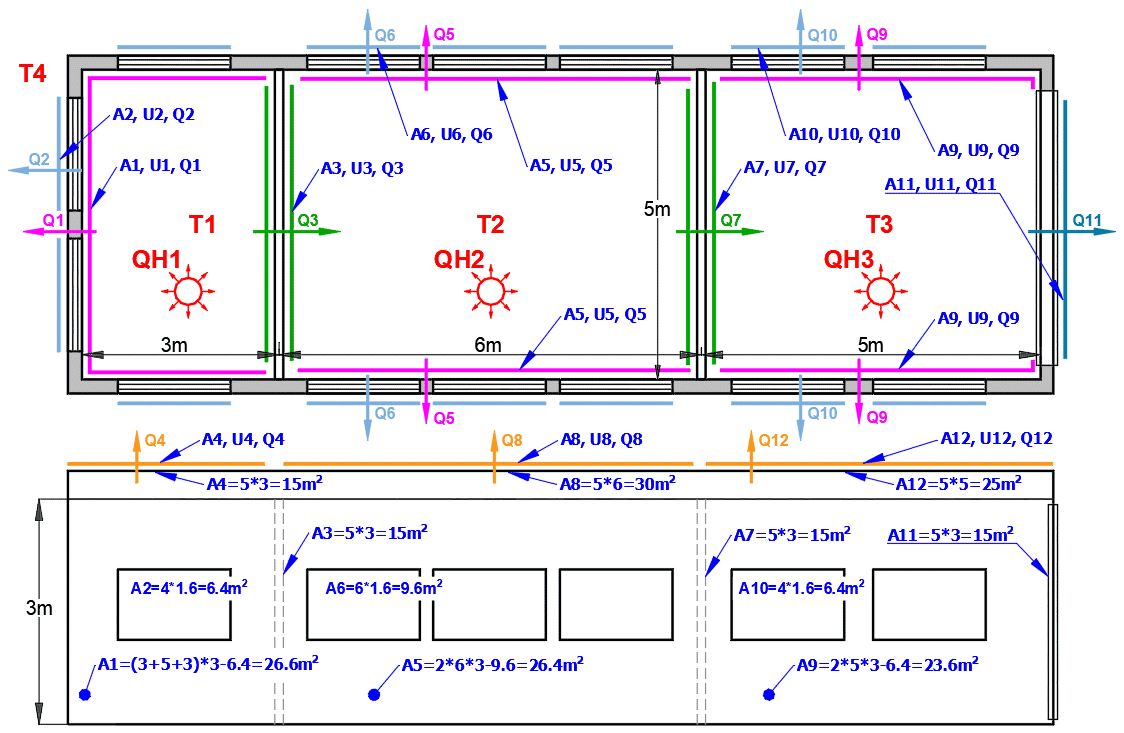
V odstavci [4.0] jsou vyřešené součinitele přestupu tepla U pro jednotlivé stěny
a jsou uložené v seznamu řešených stěn.
1. Nastavte jaké hodnoty budou z vyřešených stěn přeneseny do tabulky.
2. Postupně načtěte informace stěn pro jednotlivé místnosti.
Samozřejmě, že je možné zadat hodnoty U přímo, například z
katalogu dodavatele.
3. Nastavte skutečnou plochu pro jednotlivé stěny podle obrázku (A1=26.6,
A2=6.4,.....).
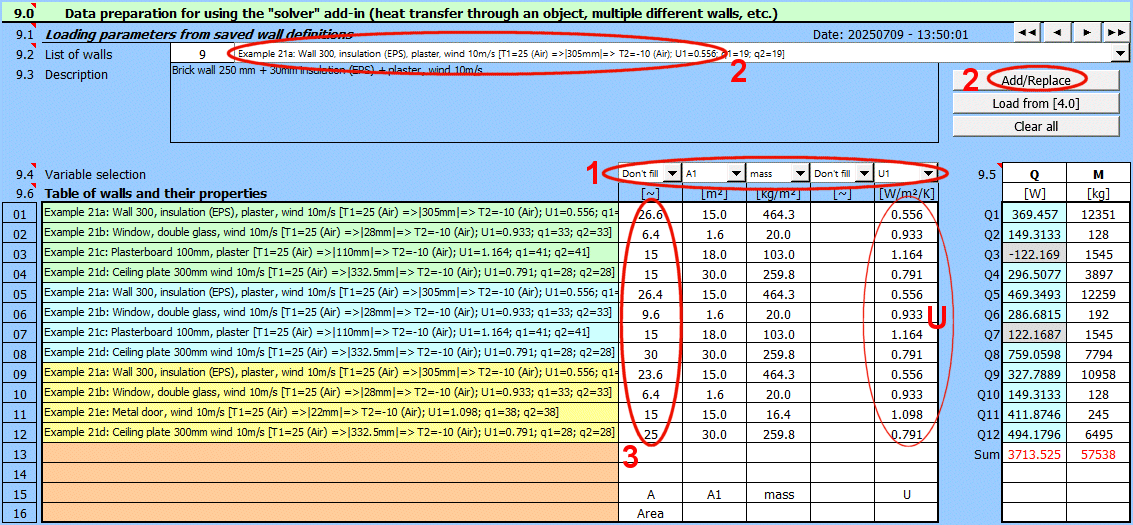
4. Definujte ve sloupci Q tepelný tok pro každou stěnu podle vzorce Q = dT * A *
U (dT ... rozdíl teplot, A ... plocha stěny, U ... součinitel přestupu tepla).
Q1 = (T1 - T4) * A1 * U1
Q2 = (T1 - T4) * A2 * U2
Q3 = (T1 - T2) * A3 * U3
Q4 = (T1 - T4) * A4 * U4
............
5. Definujte podmínky, které říkají, že tepelný tok z každé místnosti se musí
rovnat výkonu zdroje tepla.
Q1+Q2+Q3+Q4-QH1=0
Q5+Q6+Q7+Q8-Q3-QH2=0
Q9+Q10+Q11+Q12-Q7-QH3=0
6. Nastavte vhodné počáteční hodnoty zdrojů tepla (např. QH1=500, QH2=1500, QH3=1500).
7. Nastavte požadované teploty podle zadání.
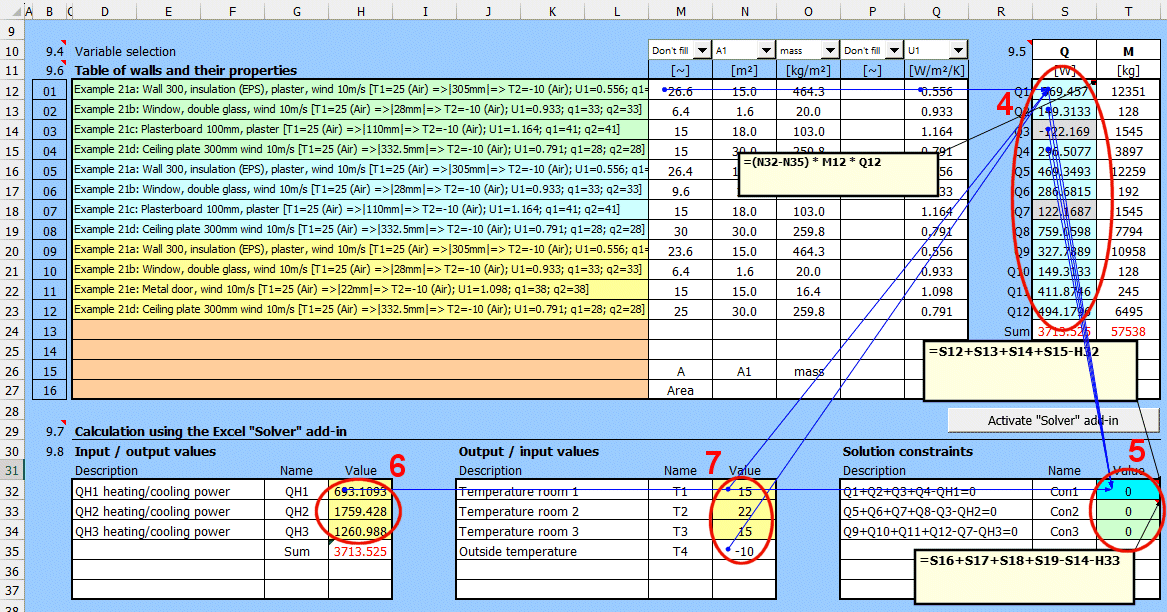
1. Spusťte doplňek "Solver" (Excel menu "Data").
2. Zadejte buňku a hodnotu, které má být dosaženo: "Set objective:".
3. Zadejte buňky, které se mají měnit: "By Changing Variable Cells:".
4. Přidejte další podmínky, které mají být splněné: "Subject to the
Constraints:".
5. Spusťte řešení úlohy: "Solve".
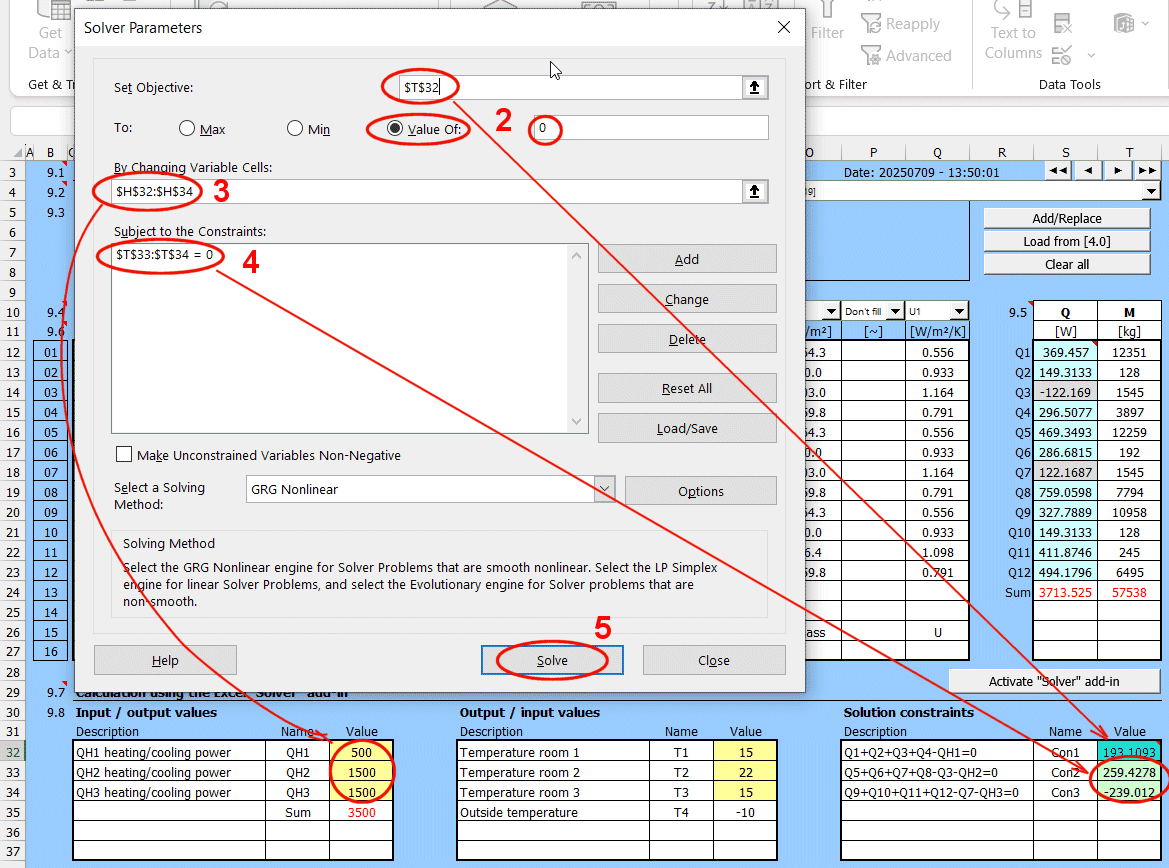
Po ukončení řešení by se měly změnit požadované hodnoty (3) a (4) a zobrazí se
dialog.
1. Zvolte uchování řešení.
2. Potvrďte: "OK".
3,4. Výsledky řešení.
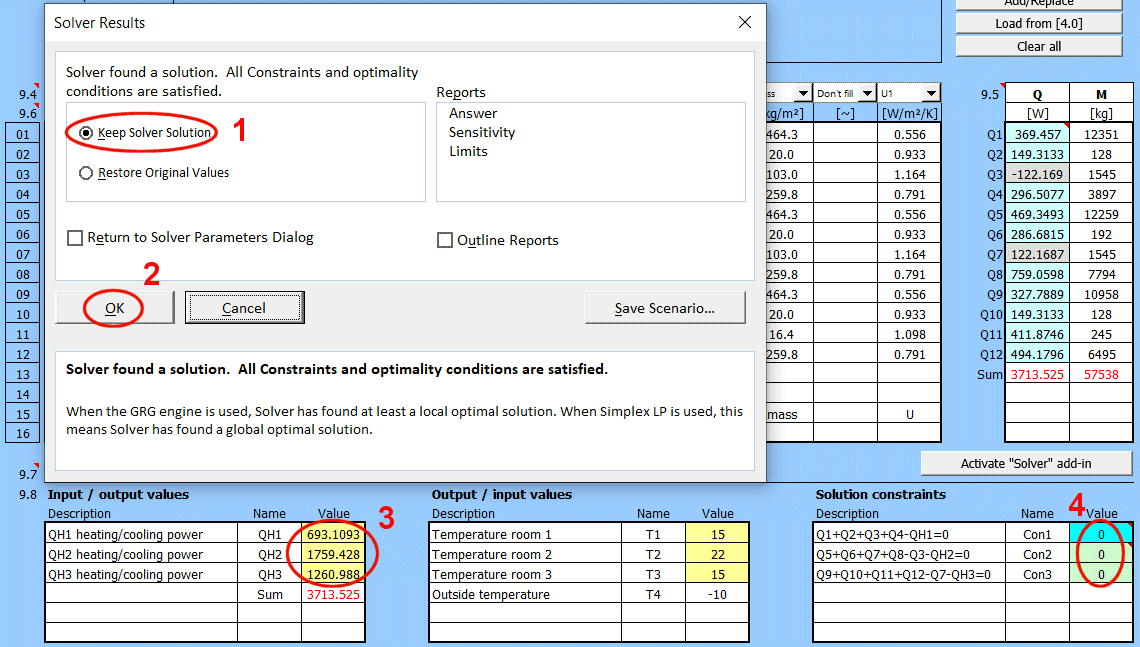
Stejným způsobem se řeší úloha B, ve které se pro zadané výkony topení (3) mění teploty místností T1,T2,T3.
Informace o nastavení parametrů výpočtu a nastavení jazyka naleznete v dokumentu "Nastavení výpočtů, změna jazyka".
Všeobecné informace o tom, jak je možné měnit a rozšiřovat sešity výpočtu, jsou uvedeny v dokumentu "Úpravy sešitu (výpočtu)".
Literatura:
EN
[01] YUNUS A. ÇENGEL, AFSHIN J. GHAJAR: Heat and Mass Transfer: Fundamentals
& Applications, 5th Edition, McGraw-Hill Education.
[02] YUNUS A. ÇENGEL: Heat Transfer a Practical Approach, Second Edition.
[03] MORAN, M.J., SHAPIO, H.N.: Fundamentals of engineering thermodynamics. 8th
Edition New York: John Wiley a sons, 1990.
[04] DEWITT, BERGMAN, LAVINE: Fundamentals of Heat and Mass Transfer 6th Edition
[05] WARREN M.ROHSENOW, JAMES R.HARTNETT, YOUNG I.CHO: Handbook of Heat
Transfer, 3th Edition, McGraw-Hill
[06] SCHLUNDER, BELL, HEWITT, SPALDING: Heat Exchanger
Design Handbook, VDI-Verlag GmbH, 1983.
[07] LOIS THEODORE: Heat Transfer Applications for the
Practicing Engineer, John Wiley & Sons, Inc., 2011.
[08] MYER KUTZ: Heat-Transfer Calculations,
McGraw-Hill
[09] HOLMAN, J.P.: Heat Transfer, 10th. Edition, New
York: McGraw-Hill
[10] HOLMAN, J.P. Thermodynamics. 4th. New York:
McGraw-Hill Book Company, 1988. 780 s. ISBN 0-07-029633-2.
[11] MOHAMED M. EL-AWAD: Optimisation Analyses of
Fluid- Thermal Systems Using Excel,
[12] FRANK KREITH, RAJ MANGLIK, MARK BOHN: Principles
of Heat Transfer, Cengage Learning, Inc., 2011
CZ
[13] HORÁK VLADIMÍR, STŘEDA IVO: Mechanika tekutin
- Termomechanika, Strojírenská příručka, Scientia sro.
[14] RANEVI,K. Termodynamické tabulky. 1.vyd.
Bratislava: ALFA 1984. 313s. [L5] HAEK, P. Tabulky pro tepelnou techniku. 1
.vyd. VB Ostrava, 1980, 247 s.
[15] SAZIMA,M., KMON1OEK,V., SCHNELER,J. Teplo. 1.vyd.
Praha: SNTL, 1989. 588 s. Technický průvodce. ISBN 80-03-00043-2.
[16] M.A.MICHEJEV: Základy sdílení tepla, Průmyslové
vydavatelství, 1952
[17] PETRAK,J., DVOAK, Z., KLAZAR, L., SYNEK, V.
Chiadivo R134a, (1.vyd.) VUT, 1993. 72s.
[18] MIROSLAV JÍLEK, ZDENĚK RANDA: Termomechanika -
sbírka příkladů, ČVUT, 2004
Normy:
ASTM C1340-2015 ... Estimation of Heat Gain or Loss Through Ceilings Under
Attics Containing Radiant Barriers...
ISO 12241:2022
Tepelněizolační výrobky pro zařízení budov a průmyslové instalace - Pravidla
výpočtu
Thermal insulation for building equipment and industrial installations —
Calculation rules
Isolation thermique des équipements de bátiments et desinstallations
industrielles — Méthodes de calcul
Wärmedammung an haus- und betriebstechnischen Anlagen — Berechnungsregeln
^